自己有网站 做app吗网站排名优化服务

思路：01背包是所有背包问题的基础，第一次看到比较懵，完全不知道dp数据怎么设置。具体分析还是dp五部曲，首先是dp数据，先想本题需要求的内容，即给定背包容量下，求能放置物品的最大价值和，因此想到的数据存放内容肯定是最大价值和，但本题有容量和物品两个维度，而之前的题目都只有一个维度，故需要用到二维数据，dp[i][j]表示从下标0-i物品中选择任意物品放入容量为j的背包中，能得到的最大价值和；

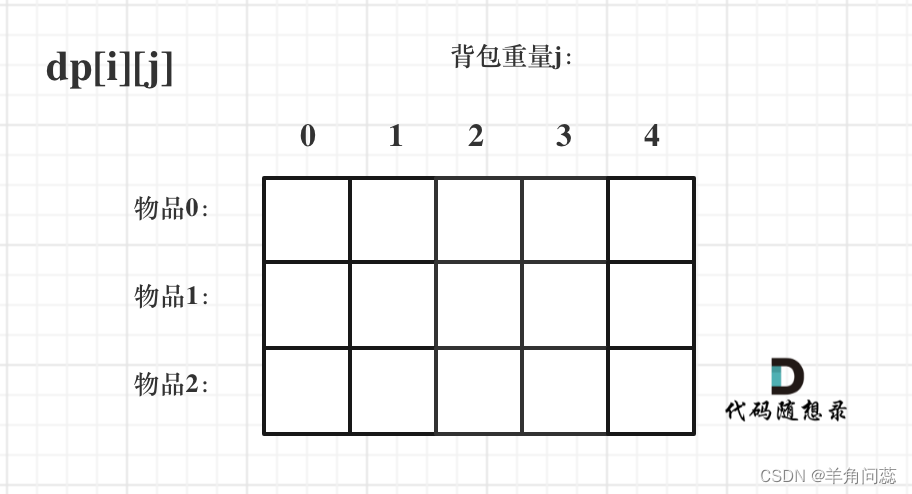
然后第二步递推公式，要递推考虑第i个物品，有两种情况，首先是不放i物品，这时候dp[i][j]=dp[i-1][j]，与前i-1个物品的结果相同，然后是放i物品，这时候背包还剩下的重量为j-weight[i]，然后在这些重量中放置前i-1个物品，dp[i][j]=dp[i-1][j-weight[i]]+value[i]，最终递推即在这两个里取最大值，如果物品i本来就放不进去，那么就只有第一种情况；第三部dp初始化，首先是j=0的时候，背包放不了任何东西，故dp[i][0]=0，然后是i=0即只有物品0的时候，这时候就是看背包能不能放下weight[0]，如果放得下则为weight[0]，否则为0，其他都被初始化为0；第四步为确定遍历顺序，先遍历物品和背包都可以，因为都是左上推右下，我们就先遍历物品；举例略。时间复杂度O(mn)。

#include<iostream>
#include<cstring>
using namespace std;int maxValue(int n,int m,int space[],int value[]){int dp[m][n+1];//空间需要0-n,物品从0-m-1即可memset(dp,0,sizeof(dp));for(int i=1;i<=n;i++){//初始化物品0if(space[0]<=i){//物品0可以放进背包了dp[0][i]=value[0];}}for(int i=1;i<m;i++){for(int j=1;j<=n;j++){if(space[i]>j){//物品i无法先放进去dp[i][j]=dp[i-1][j];}else{//先放物品idp[i][j]=max(dp[i-1][j],dp[i-1][j-space[i]]+value[i]);}}}return dp[m-1][n];
}int main(){int n,m;while(cin >> m >> n){int space[m],value[m];for(int i=0;i<m;i++){cin >> space[i];}for(int i=0;i<m;i++){cin >> value[i];}cout << maxValue(n,m,space,value) << endl;}return 0;
}

我比较喜欢的ACM写法是把解题过程抽象成一个函数，数据输入全部在main中完成，标答是在solve()中处理输入。

看标答发现可以把数据压缩成一维，因为递推公式的i都是i-1，我们可以只保留每一行，也就是滚动数组。新的一维dp数组dp[j]表示容量为j的背包能装入的最大价值；递归公式，还是看物品i能不能先放进去，如果不能，那么dp[j]就不变，如果能放先放进去，那么就比较当前dp[j]和dp[j-weight[i]]+value[i]，取最大值；初始化，只初始化一行，dp[0]肯定为0，其他下标位置，也初始化为0，因为后面递推过程中会逐渐取最大值；遍历顺序，这是一维写法比较困难的地方，必须从背包容量从大到小遍历，因为如果从小到大，会把前面的背包放入两次，比如w[0]=1,v[0]=15，在计算dp[1]的过程中即为dp[0]+v[0]=15，而对dp[2]，如果取dp[1]+value[0]=30，会算两次物品0，而从大到小遍历，我们一开始没有放入物品，dp[0]初始化均为0，dp[2]=dp[1]+value[0]=15，因为在这一次遍历中，还没有考虑到dp[1]，后续计算dp[1]=dp[0]+value[0]=15，故不会重复放入，而之前的二维数组，每一次dp[i][j]都由上一层计算而来，本层的没有被覆盖过，因此不存在重复计算问题；举例略。主要就是为了避免本层覆盖的问题，因为dp数组都是由上一层计算的。一维滚动数组写法的代码如下：

int maxValue(int n,int m,int space[],int value[]){int dp[n+1]={0};for(int i=1;i<=n;i++){//初始化if(space[0]<=i){//物品0可以放进背包了dp[i]=value[0];}}for(int i=1;i<m;i++){for(int j=n;j>=0;j--){if(space[i]<=j){//物品i能先放进去dp[j]=max(dp[j],dp[j-space[i]]+value[i]);}}}return dp[n];
}

真正理解需要画图分析。一维写法空间复杂度大幅下降，需要掌握。

思路：本题的第一想法就是使用回溯暴力搜索和为sum/2的所有元素，如果找到返回true。能不能套用01背包问题呢，把数组中所有元素对应为物品，每个物品只能放入一次，背包的容量为sum/2，放入的物品重量为元素的数值，价值也为元素的数值，需要保证背包正好装满。对应dp五部曲，首先是dp数组，dp[j]表示背包容量为j时，能放入最大价值，若背包容量为target，则dp[target]即背包装满后的容量，dp[target]=target即装满，如果装不满，即价值未达到要求，dp[target]<target；递推公式，物品i能放进去的时候，dp[j]=max(dp[j],dp[j-nums[i]]+nums[i])，因为物品i的weight和value都是nums[i]；初始化，由于题目的价值都是非负，dp直接全初始化为0即可；递推顺序，按重量从大到小；举例略。时间复杂度O(nm),m为和。

class Solution {
public:bool canPartition(vector<int>& nums) {int sum=accumulate(nums.begin(),nums.end(),0);//库函数求和if(sum%2==1){//和为奇数直接排除return false;}int target=sum/2;vector<int> dp(20001,0);//由题意知最大的和不会超过20000int n=nums.size();for(int i=0;i<n;i++){for(int j=target;j>=nums[i];j--){dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);}}if(dp[target]==target){//容量为target的背包装完后价值恰好为target，即表示装满return true;}return false;}
};

本题的难点就在于将原问题和01背包对应起来，主要是装满如何想到，即把价值和重量都定义成元素的值，装满target重量即为target容量的背包能装的最大价值恰好为target，即dp[target]=target。