四川省人力资源和社会保障厅关键词优化seo公司
算法提高-树状数组
- 241. 楼兰图腾(区间求和 + 单点修改)
- 242. 一个简单的整数问题(差分+推公式 实现 维护区间修改+单点求和)
- 243. 一个简单的整数问题2(区间修改和区间求和)
- AcWing 244. 谜一样的牛(用二分查找想要的状态 + 树状数组动态记录当前区间的状态)
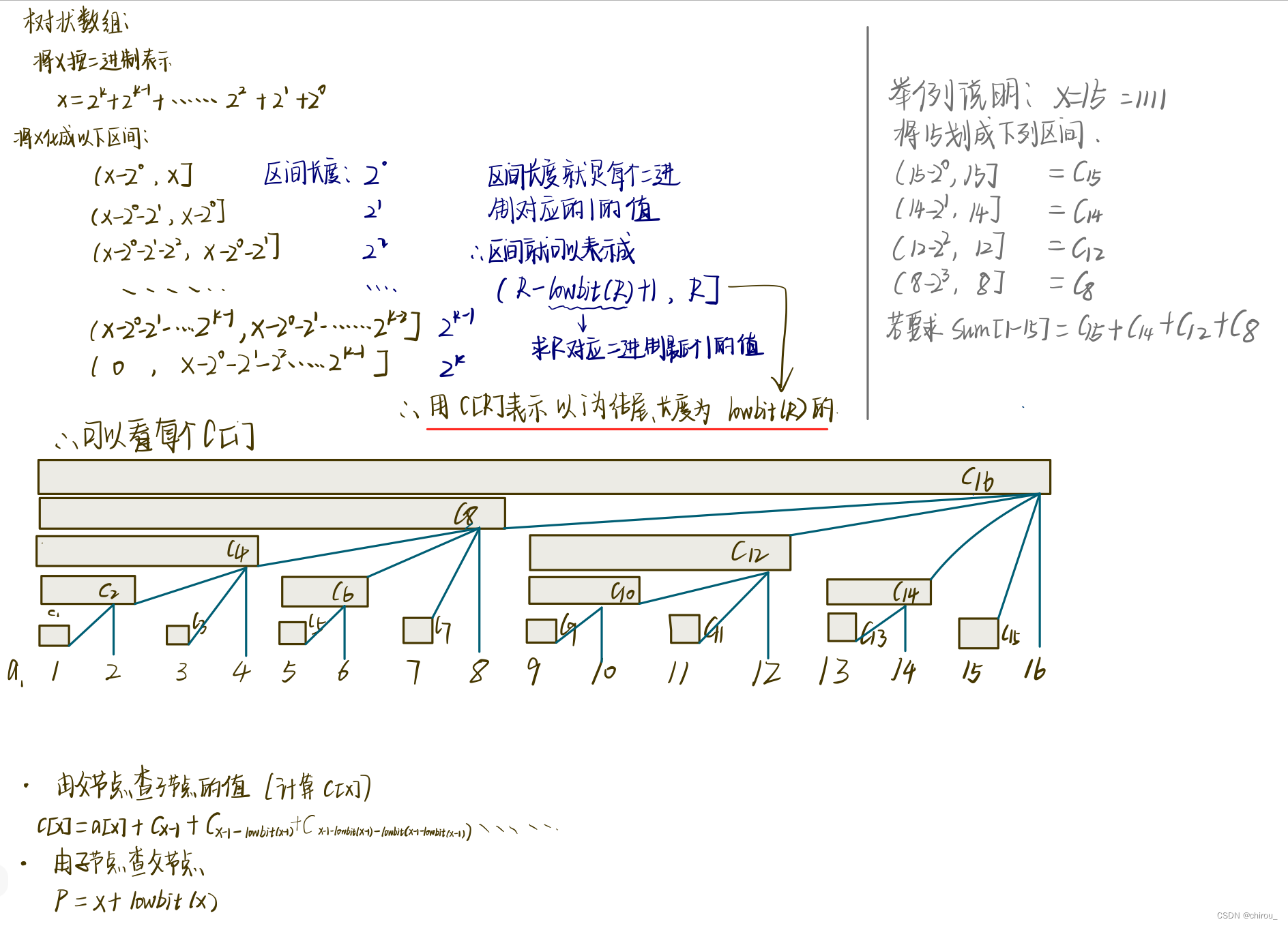
树状数组的两个作用
- 快速求区间和
- 快速修改某一个数同时可以快速修改区间和
- tr[i]记录的区间的长度是lowbit(i)
241. 楼兰图腾(区间求和 + 单点修改)
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;
typedef pair<int, int> pii;
const int N = 2e5 + 10;
int tr[N];
int a[N];
int n;
int lowbit(int x)
{return x & -x;
}
void add(int x, int c)
{for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}int sum(int x)//统计下标为1-x的前缀和
{int res = 0;for (int i = x; i; i -= lowbit(i)) res += tr[i];return res;
}void solve()
{scanf("%d", &n);vector<int> Greater(N+1);//y的取值正好也是1-n,否则就需要离散化了vector<int> lower(N+1);for (int i = 1; i <= n; ++ i) scanf("%d", &a[i]);for (int i = 1; i <= n; ++ i){int y = a[i];Greater[i] = sum(n) - sum(y);//遍历到a[i]的时候,下标为(1, n)在n~y+1之间的数有几个lower[i] = sum(y-1);遍历到a[i]的时候,从1~y-1之间的数有几个add(y, 1);//遍历完a[i]后,将a[i]出现的次数加1,我们前缀和sum}memset(tr, 0, sizeof tr);typedef long long LL;LL res1 = 0, res2 = 0;for (int i = n; i; -- i)//逆向遍历{res1 += Greater[i] *(LL)(sum(n) - sum(a[i]));//记录下标在(n, i)之间有多少个数字大于a[i]res2 += lower[i] * (LL)(sum(a[i]-1));add(a[i], 1);}cout << res1 << " "<< res2;
}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;// cin >> T;while (T --) solve();return 0;
}
242. 一个简单的整数问题(差分+推公式 实现 维护区间修改+单点求和)
树状数组擅长的是单点加然后求区间和,本题是区间加然后求单点和;
- 在原数组上求某个点的值 = 求差分数组的前缀和
- 在原数组上更改某个区间的值 = 修改差分数组两个端点的值
为了将我们对原数组的操作转化为经典的树状数组的操作(修改单点的值, 求一个区间的和),我们这里tr[]维护的就是a[]的差分数组。
差分数组b[]和原数组a[]的关系
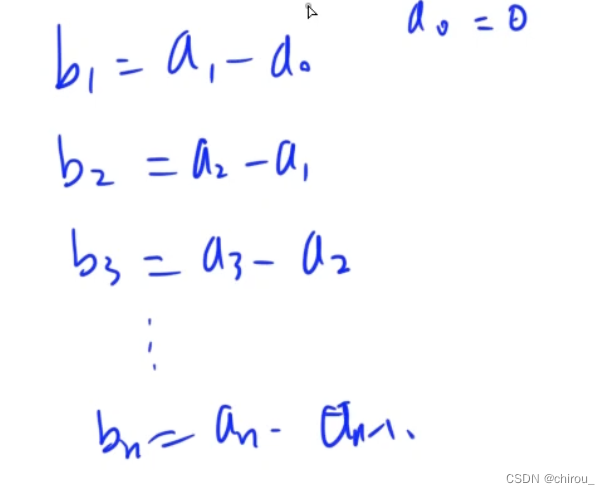
用树状数组实现前缀和 脱裤子放屁多此一举版本
事实上能写出这种代码还是没有理解树状数组的作用是啥,树状数组的作用就是区间求和和单点修改,使得区间求和和单点修改的复杂度都不至于太慢。
数组的区间求和复杂度是n,单点修改复杂度是1
前缀和的区间求和复杂度是1,单点修改的复杂度是n;
树状数组的区间求和和单点修改的复杂度都是logn。
本题是区间修改和单点求和,这显然不是树状数组的正常操作,即我们树状数组不能去维护a[],而是应该去维护他的差分数组b[]
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
using namespace std;
typedef pair<int, int> pii;
const int N = 1e5 + 10;
typedef long long LL;
int a[N];
LL tr[N];
int n, m;
// 10 5
// 1 2 3 4 5 6 7 8 9 10
// Q 4
// Q 1
// Q 2
// C 1 6 3
// Q 2
int lowbit(int x)
{return x & -x;
}
void add(int x, int c)
{for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
LL presum(int x)
{LL res = 0;for (int i = x; i; i -= lowbit(i)) res += tr[i];return res ;
}
void solve()
{cin >> n >> m;for (int i = 1; i <= n; ++ i) {cin >> a[i];add(i, a[i]);}char op[2];while (m -- ){cin >> op;int l, r, x;if (*op == 'Q'){cin >> x;cout << presum(x) - presum(x - 1)<< endl;//这不就是前缀和么,虽然查找是1,但是修改就很大了,} //我用树状数组多次一举的话更大else {cin >> l >> r >> x;for(int i = l; i <= r; ++ i)//可以看到前缀和的话修改操作的复杂度是n^2logn{add(i, x);}}}}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;// cin >> T;while (T --) solve();return 0;
}
ac代码
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
using namespace std;
typedef pair<int, int> pii;
const int N = 1e5 + 10;
typedef long long LL;
int a[N];
LL tr[N];
int n, m;
// 10 5
// 1 2 3 4 5 6 7 8 9 10
// Q 4
// Q 1
// Q 2
// C 1 6 3
// Q 2
int lowbit(int x)
{return x & -x;
}
void add(int x, int c)
{for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
LL presum(int x)
{LL res = 0;for (int i = x; i; i -= lowbit(i)) res += tr[i];return res ;
}
void solve()
{cin >> n >> m;for (int i = 1; i <= n; ++ i) {cin >> a[i];add(i, a[i] - a[i - 1]);}char op[2];while (m -- ){cin >> op;int l, r, x;if (*op == 'Q'){cin >> x;cout << presum(x) << endl;//这不就是前缀和么,虽然查找是1,但是修改就很大了,} //我用树状数组多次一举的话更大else {cin >> l >> r >> x;add(l, x);add(r + 1, -x);}}}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;// cin >> T;while (T --) solve();return 0;
}
243. 一个简单的整数问题2(区间修改和区间求和)
- 区间求和 + 单点修改 = 普通树状数组(对前缀和以及普通数组的优化)
- 区间修改 + 单点求和 = 树状数组维护差分数组(这样的话区间修改就可以对应到单点修改差分数组,单点求和就可以对应到区间求差分数组的和)
- 区间求和 + 区间修改 = 维护两个树状数组,一个用维护差分数组b[i](可以做到区间修改),一个维护i*b[i],推公式可以得出对a[]数组区间求和就是下面这个公式

还不懂的话可以看下面这段解释


因为多维护一个i * b[i], add函数里面的c可能会爆int,所以要强转一下
经验:
- 如果过了样例数据也过了大部分,那就看一下是不是没开longlong
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
using namespace std;
typedef pair<int, int> pii;
const int N = 1e5 + 10;
typedef long long LL;
int a[N];
LL tr[N], tri[N];
int n, m;int lowbit(int x)
{return x & -x;
}
void add(LL tree[], int x, LL c)//开LL
{for (int i = x; i <= n; i += lowbit(i)) tree[i] += c;
}
LL presum(LL tree[], int x)
{LL res = 0;for (int i = x; i; i -= lowbit(i)) res += tree[i];return res ;
}
LL prefixsum (int x)
{return presum(tr, x) * (x + 1) - presum(tri, x);
}
void solve()
{cin >> n >> m;for (int i = 1; i <= n; ++ i) {cin >> a[i];add(tr, i, a[i] - a[i - 1]);add(tri, i, (LL)i * (a[i] - a[i - 1]));//开LL}char op[2];while (m -- ){cin >> op;int l, r, x;if (*op == 'Q'){cin >> l >> r;cout << prefixsum(r) - prefixsum(l - 1) << endl;}else {cin >> l >> r >> x;add(tr, l, x); add(tr, r + 1, -x);add(tri, l, l * x); add(tri, r + 1, (r + 1) * (-x));}}}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;// cin >> T;while (T --) solve();return 0;
}
AcWing 244. 谜一样的牛(用二分查找想要的状态 + 树状数组动态记录当前区间的状态)
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
using namespace std;
typedef pair<int, int> pii;
const int N = 1e5 + 10;
int tr[N], pos[N];
int n;
// 5
// 1
// 2
// 1
// 0
int lowbit(int x)
{return x & -x;
}
void add(int x, int c)
{for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
int presum(int x)//树状数组的本质就是求前缀和
{int sum = 0;for (int i = x; i; i -= lowbit(i)) sum += tr[i];return sum;
}
int find(int k)//
{int l = 1, r = n;while (l < r){int mid = l + r >> 1;if (presum(mid) >= k) r = mid;//求高度为1到n之间高度为mid的牛之前有多少头牛还没有被用过,其实也就是求高度为mid的牛在当前剩下的牛中是否为第k高的牛else l = mid + 1; //因为我们求的是第一个第k高的牛,那么当前搜索的高度为mid的牛一定是还没有确定位置的牛}return l;
}
void solve()
{cin >> n;add(1, 1);for (int i = 2; i <= n; ++ i){cin >> pos[i];add(i, 1);//单点修改tr[i] = 1,同时对i后面的树状数组造成影响。树状数组的本质就是前缀和,同时单点修改的复杂度也不低不高}vector<int> ans(n + 1);for (int i = n; i; -- i){int height;height = find(pos[i] + 1);//找到当前在剩下的牛中第pos + i高的牛,它的高度是heightans[i] = height;add(height, -1);//表明这个height这个高度的牛已经用过了,他会对1-n中高度 >height的牛的前缀和造成影响}for (int i = 1; i <= n; ++ i) cout << ans[i] << endl;
}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;// cin >> T;while (T --) solve();return 0;
}