济南哪里有做网站的百度手机下载安装

在Unity中，向量无处不在，我想很多人都使用过向量类的内置方法 normalized() 吧，我们都知道该方法是将其向量归一化从而作为一个方向与速度相乘，以达到角色朝任一方向移动时速度都相等的效果，但内部具体是如何将该向量进行归一化的呢，本篇我们就来揭晓这个答案。

1. 相关概念

在学习向量的运算之前，我们先要了解一些有关概念：

标量（scalar）是一个只有大小，没有方向的物理量。

向量（vector）是一个有长度，也有方向的有向线段。

向量的模（magnitude）指的这个向量的长度。一个向量的长度可以是任意的非负数。模式一个标量。

向量的方向（direction）描述了这个向量在空间的指向。

2. 向量和标量的乘法/除法

以三维向量为例，向量和标量的乘法公式如下：

类似的，向量也可以被一个非零的标量相除，这等同于和这个标量的倒数相除：

 

 下面是两个简单的例子：

 

3. 向量之间的加法和减法 

 我们可以对两个向量进行相加或相减，其结果是一个相同维度的新向量。只需要把两个向量的对应分量进行相加或相减即可，公式如下：

 

下面是两个简单的例子：

 

 

 4. 向量的模

我们以三维向量为例，计算一个向量的模公式如下：

 我们以一个二维向量(1, 1)为例，模的计算方式如下：

 5. 向量的归一化

向量归一化（normalized vector）是指将该向量的模变为1，模为1的向量被称为单位向量（unit vector）。对任何给定的非零向量，把它转换成单位向量的过程就被称为归一化（normalization）。

通常，我们在向量的头上添加一个带帽符号来表示单位向量，例如。为了对向量进行归一化，我们可以将向量除以该向量的模来得到，公式如下：

 我们以一个二维向量(1, 1)为例，该向量归一化的计算方式如下：

6. 向量之间的乘法

6.1. 点积

点积（dot product）的名称来源于这个运算符号：。点积的公式有两种形式，我们先看第一种公式：

它还有第二个公式：

由此公式我们可以得出：

 

 当a、b两个向量都为单位向量，也就是和都为1时，公式又可以简化为：

因此：

 

6.2. 叉积

叉积（cross product）的名称来源于它的符号：，同样这个叉号也不能省略它的计算公式为：

我们用一张图就可以清晰的描述它的运算规律：

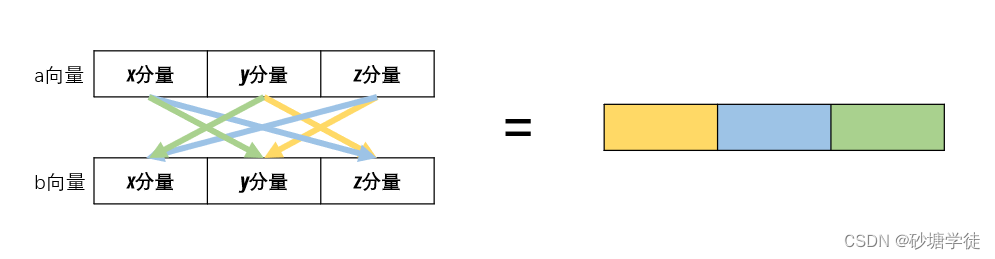
计算出来的向量是垂直于a、b所构成的平面的法向量。