企业建站公司案例吉林关键词优化的方法
文章目录
- 相关链接
- 什么时候使用二分答案?
- 题目列表
- 最大化最小化相关题目列表📕
- 2439. 最小化数组中的最大值
- 解法1——二分答案
- 解法2——分类讨论O(n)
- 2513. 最小化两个数组中的最大值(二分答案+lcm+容斥原理)🐂好题!
- 相似题目(容斥原理+二分查找)
- 878. 第 N 个神奇数字
- 1201. 丑数 III
- 2517. 礼盒的最大甜蜜度(二分答案)
相关链接
【力扣周赛】第 362 场周赛(⭐差分&匹配&状态压缩DP&矩阵快速幂优化DP&KMP)里面有一些二分答案的题目。
【力扣周赛】第 363 场周赛(完全平方数和质因数分解) T3是二分答案。
什么时候使用二分答案?
看到「最大化最小值」或者「最小化最大值」就要想到二分答案,这是一个固定的套路。
或者
答案不好直接求,但是可以判断某个数字是否可以满足题目要求且单调时。
具体看下面例题体会一下即可。
题目列表
最大化最小化相关题目列表📕
题目列表来源:https://leetcode.cn/problems/maximize-the-minimum-powered-city/solutions/2050272/er-fen-da-an-qian-zhui-he-chai-fen-shu-z-jnyv/

2439. 最小化数组中的最大值
https://leetcode.cn/problems/minimize-maximum-of-array/
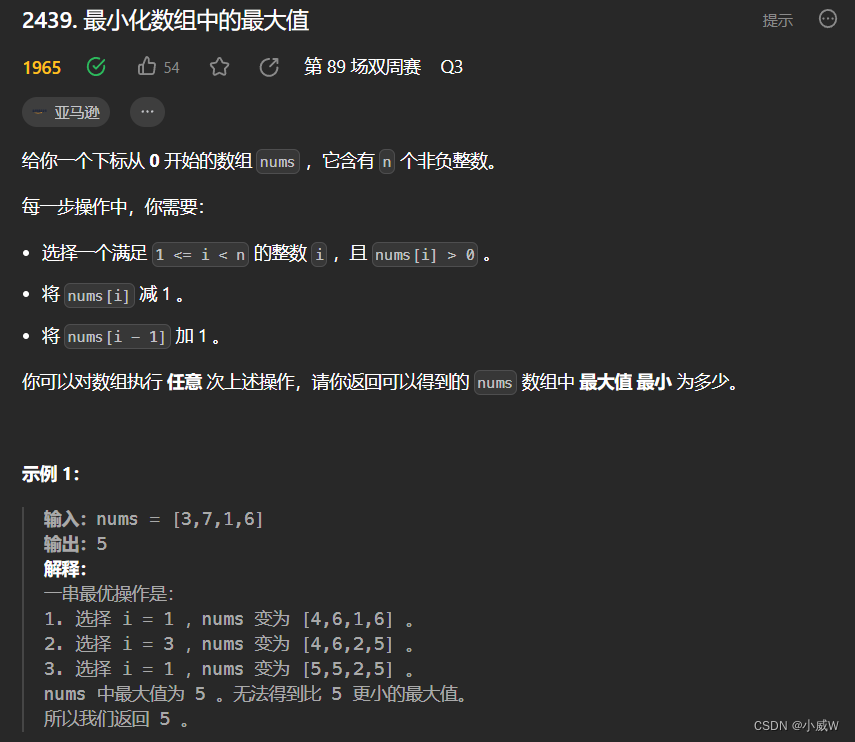
提示:
n == nums.length
2 <= n <= 10^5
0 <= nums[i] <= 10^9
解法1——二分答案
class Solution {public int minimizeArrayValue(int[] nums) {int l = Integer.MAX_VALUE, r = Integer.MIN_VALUE;for (int x: nums) {l = Math.min(l, x);r = Math.max(r, x);}while (l < r) {int mid = l + r >> 1;if (check(mid, nums)) r = mid;else l = mid + 1;}return l;}public boolean check(int k, int[] nums) {if (nums[0] > k) return false;long d = k - nums[0]; // 使用long防止溢出for (int i = 1; i < nums.length; ++i) {if (nums[i] <= k) d += k - nums[i];else {d -= nums[i] - k;if (d < 0) return false;}}return true;}
}
解法2——分类讨论O(n)
首先最大值的最小值是 nums[0]。
对于 nums[1],当其 < nums[0] 时,答案还是 nums[0];当其 > nums[0] 时,则答案是两者的平均向上取整。
class Solution {public int minimizeArrayValue(int[] nums) {long mx = 0, sum = 0;for (int i = 0; i < nums.length; ++i) {sum += nums[i];// (sum + i) / (i + 1) 是因为要向上取整mx = Math.max(mx, (sum + i) / (i + 1)); }return (int)mx;}
}
2513. 最小化两个数组中的最大值(二分答案+lcm+容斥原理)🐂好题!
https://leetcode.cn/problems/minimize-the-maximum-of-two-arrays/
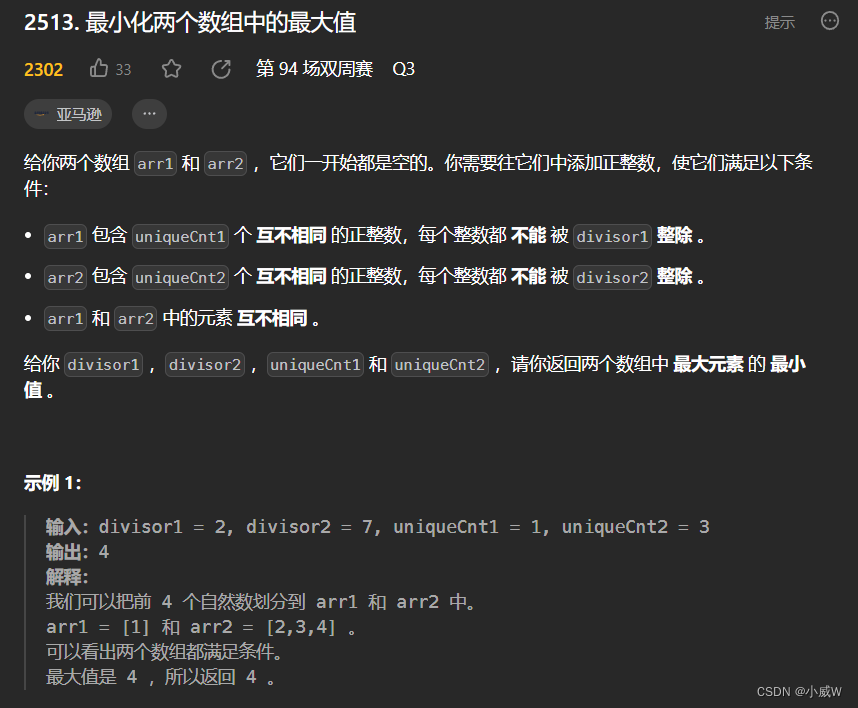
提示:
2 <= divisor1, divisor2 <= 10^5
1 <= uniqueCnt1, uniqueCnt2 < 10^9
2 <= uniqueCnt1 + uniqueCnt2 <= 10^9
二分答案。
class Solution {public int minimizeSet(int divisor1, int divisor2, int uniqueCnt1, int uniqueCnt2) {long l = 0, r = (long)Integer.MAX_VALUE;while (l < r) {long mid = l + r >> 1;// 两个数组不能选择的数字数量long x = mid / divisor1, y = mid / divisor2, z = mid / lcm(divisor1, divisor2);long sum = uniqueCnt1 + uniqueCnt2 + z; // 至少需要的数字数量// arr1不能使用的,看arr2能不能使用;反之同理sum += Math.max(0, x - z - uniqueCnt2) + Math.max(0, y - z - uniqueCnt1);if (sum <= mid) r = mid;else l = mid + 1;}return (int)l;}// 最小公倍数public long lcm(long x, long y) {return x / gcd(x, y) * y;}// 最大公因数public long gcd(long x, long y) {return y == 0? x: gcd(y, x % y);}
}
相似题目(容斥原理+二分查找)
878. 第 N 个神奇数字
https://leetcode.cn/problems/nth-magical-number/
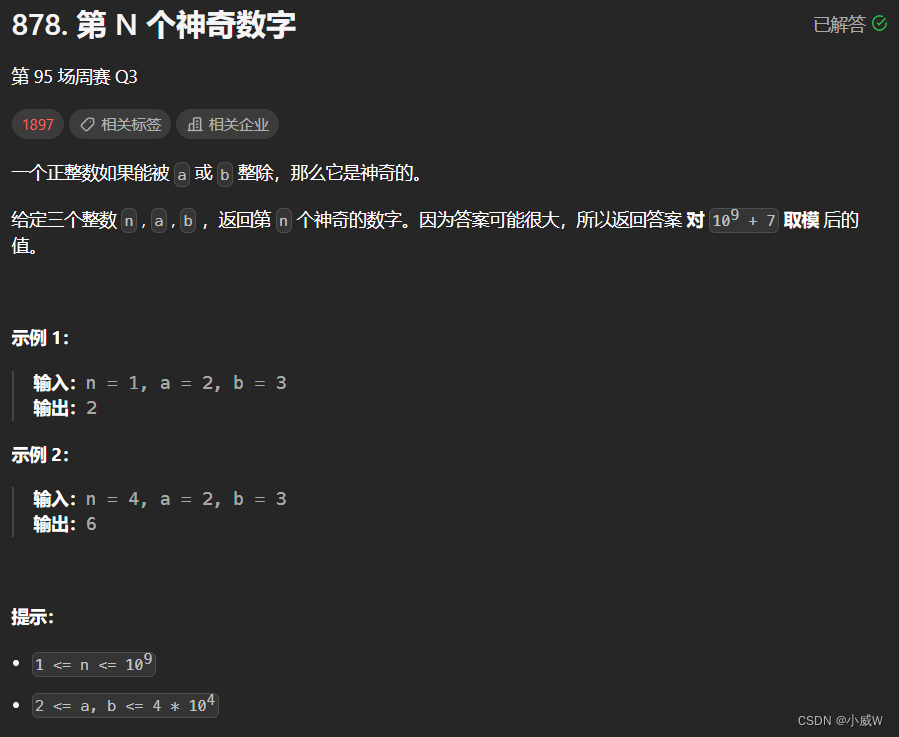
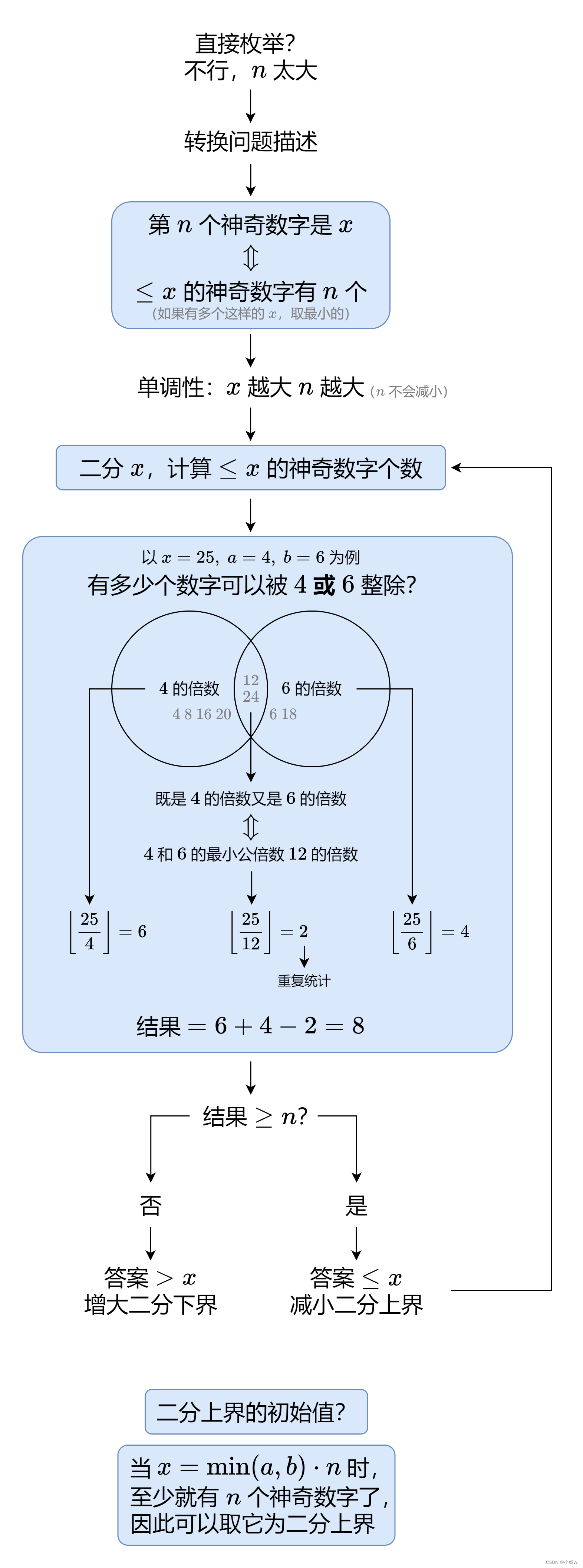
答案可能会很大,所以先将变量设置成 long 类型。
class Solution {final long MOD = (long)1e9 + 7;public int nthMagicalNumber(int n, int a, int b) {long c = lcm(a, b);long l = 2, r = Long.MAX_VALUE - 2;while (l < r) {long mid = l + r >> 1;long x = mid / a, y = mid / b, z = mid / c;long s = x + y - z; // 容斥原理if (s < n) l = mid + 1;else r = mid;}return (int)(l % MOD);}public long lcm(long a, long b) {return a * b / gcd(a, b);}public long gcd(long a, long b) {return b == 0? a: gcd(b, a % b);}
}
1201. 丑数 III
https://leetcode.cn/problems/ugly-number-iii/description/
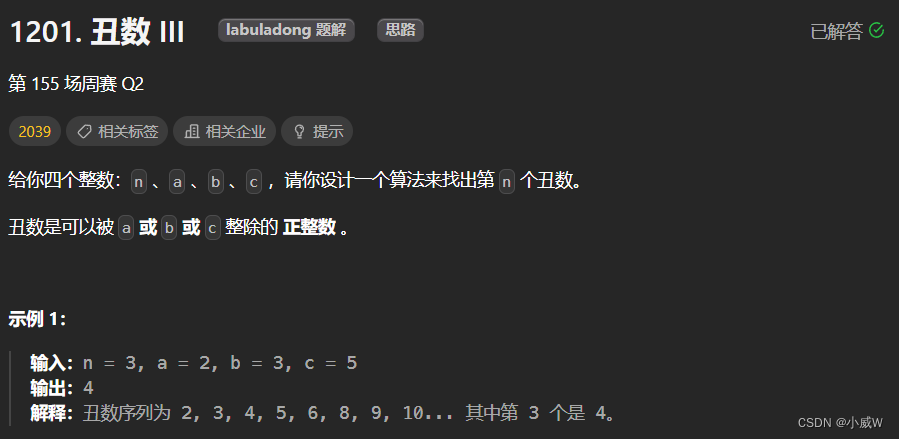
提示:
1 <= n, a, b, c <= 10^9
1 <= a * b * c <= 10^18
本题结果在 [1, 2 * 10^9] 的范围内
注意这题也要先使用 long 数据类型。
class Solution {public int nthUglyNumber(int n, int a, int b, int c) {// 注意要转成longlong x = lcm(a, b), y = lcm(b, c), z = lcm(a, c), q = lcm(x, y);long l = 1, r = (long)2e9;while (l < r) {long mid = l + r >> 1;long aa = mid / a, bb = mid / b, cc = mid / c, xx = mid / x, yy = mid / y, zz = mid / z, qq = mid / q;// 容斥原理long s = aa + bb + cc - xx - yy - zz + qq;if (s < n) l = mid + 1;else r = mid;}return (int)l;}// 求最小公倍数public long lcm(long a, long b) {return a / gcd(a, b) * b;}// 求最大公因数public long gcd(long a, long b) {return b == 0? a: gcd(b, a % b);}
}
2517. 礼盒的最大甜蜜度(二分答案)
https://leetcode.cn/problems/maximum-tastiness-of-candy-basket/
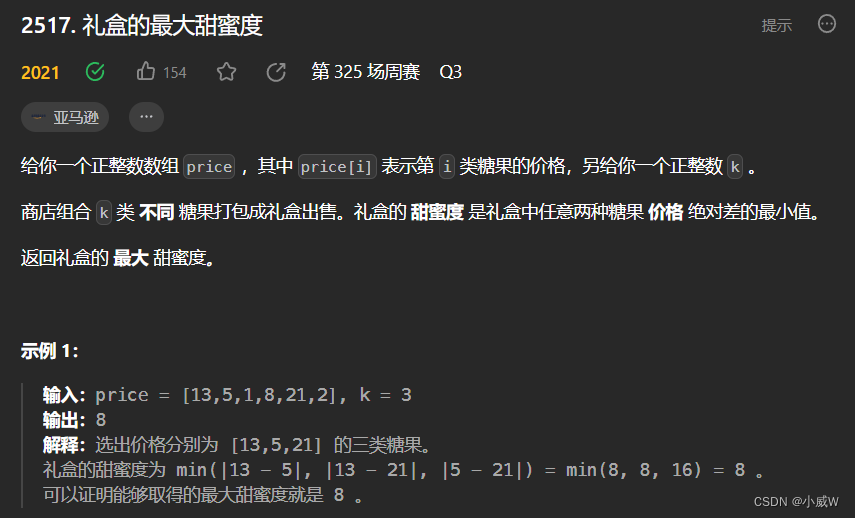
提示:
2 <= k <= price.length <= 10^5
1 <= price[i] <= 10^9
class Solution {public int maximumTastiness(int[] price, int k) {Arrays.sort(price);int n = price.length, l = 0, r = price[n - 1] - price[0];while (l < r) {int mid = l + r + 1 >> 1;int s = 1, last = price[0];for (int i = 1; i < n && s < k; ++i) {if (price[i] - last >= mid) {s++;last = price[i];}}if (s < k) r = mid - 1;else l = mid;}return l;}
}
