网站开发与维护的工资seo搜索引擎优化策略
👀樊梓慕：个人主页
🎥个人专栏：《C语言》《数据结构》《蓝桥杯试题》《LeetCode刷题笔记》《实训项目》《C++》《Linux》《算法》
🌝每一个不曾起舞的日子，都是对生命的辜负
目录
前言
1.数组分块（数组划分）
移动零
复写零
2.快慢双指针（循环往复）
快乐数
3.对撞指针->暴力枚举的优化->利用单调性
盛最多水的容器
有效三角形的个数
4.对撞指针->两数之和、三数之和、四数之和
两数之和
三数之和
四数之和
前言
💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐
《算法》专栏正式挂牌成立
- 《算法》专栏主要是会系统的梳理一些OJ题的算法思想，将他们按照解题方法的不同划分出来，然后归纳总结，当然希望大家多多收藏，以后忘了可以常回来看看！
💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐💐
本篇文章主要会讲解双指针的思想，双指针是一种非常优秀的算法思想，有对撞指针和快慢指针两种基本用法。
双指针对于有序数据的处理是比较有优势的，当你遇到有序的数据时，你可以尝试着利用双指针或者二分来解题，当然本篇文章只会讲解双指针。
那么双指针思想具体的应用，以及为什么双指针适用于有序数组的处理呢？
欢迎大家📂收藏📂以便未来做题时可以快速找到思路，巧妙的方法可以事半功倍。
=========================================================================
GITEE相关代码：🌟fanfei_c的仓库🌟
=========================================================================
1.数组分块（数组划分）
数组分块顾名思义，该类题目有一个特性就是将数组中的数据进行分类，然后将分类的数据放在不同的区域上。
移动零
移动零 - 力扣（LeetCode）
https://leetcode.cn/problems/move-zeroes/description/
给定一个数组
nums，编写一个函数将所有0移动到数组的末尾，同时保持非零元素的相对顺序。请注意 ，必须在不复制数组的情况下原地对数组进行操作。
利用数组分块的思想，我们可以将该数组划分为三个区域：非零的已处理区域、零的已处理区域、待处理区域。
三个区域恰好可以利用两个指针进行分割得到。
所以我们定义两个指针：
- cur：从左向右扫描数组（遍历数组的作用），主要用来分割已处理区域和待处理区域用；
- dest：已处理的区域内，非零元素的最后一个位置，主要用来分隔已处理区域内部非零元素和零元素。
得到三个区间：
- 非零的已处理区域：[0,dest]
- 零的已处理区域：[dest+1,cur-1]
- 待处理区域：[cur,n-1]
有了思路，画图独立完成代码，不要直接看博主的代码。
class Solution {
public:void moveZeroes(vector<int>& nums) {for (int dest = -1, cur = 0; cur <= nums.size() - 1; cur++){//如果是零就跳过，不是零进入if (nums[cur]){swap(nums[++dest], nums[cur]);}}}
};复写零
复写零 - 力扣（LeetCode）https://leetcode.cn/problems/duplicate-zeros/description/
给你一个长度固定的整数数组
arr，请你将该数组中出现的每个零都复写一遍，并将其余的元素向右平移。注意：请不要在超过该数组长度的位置写入元素。请对输入的数组 就地 进行上述修改，不要从函数返回任何东西。
我们可以先尝试着进行异地复写，然后尝试着进行原地复写，看看会发生什么问题？
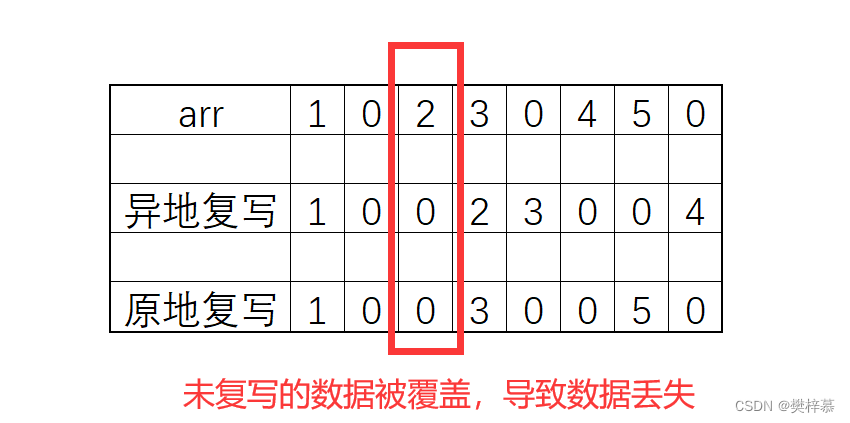
如果「从前向后」进行原地复写操作的话，由于0的出现会复写两次，导致没有复写的数「被覆
盖掉」。
因此我们选择「从后往前」的复写策略。
但是「从后向前」复写的时候，我们需要找到「最后一个复写的数」，因此我们的大体流程分两
步：
- 先找到最后一个复写的数；
- 然后从后向前进行复写操作。
这两步仍然包含一些细节需要处理，比如会不会出现越界问题等？
- cur：用来遍历数组用。
- dest：根据cur指向的指进行移动一步或两步，如果dest的位置处于最后一位或者已经越界，跳出循环，如果是越界的情况，我们需要手动将其"拉回"，然后进行从后向前的复写操作。
有了思路，画图独立完成代码，不要直接看博主的代码。
class Solution {
public:void duplicateZeros(vector<int>& arr) {int dest=-1,cur=0,n=arr.size();//1.先找到cur位置while(cur<n){if(arr[cur])dest++;elsedest+=2;if(dest>=n-1)//这里是为了及时检测是否跳出break;cur++; }//1.5判断dest位置if(dest==n){arr[dest-1]=0;dest-=2;cur--;}//2.然后向前复写while(cur>=0){if(arr[cur])arr[dest--]=arr[cur--]; else{arr[dest--]=0;arr[dest--]=0;cur--;}}}
};2.快慢双指针（循环往复）
快慢双指针基本思想：使用两个移动速度不同的指针在数组或链表等序列结构上移动。
一般什么情况下适用快慢双指针的题目呢？
这种方法对于处理环形链表或数组非常有用，或者说循环往复的数据都比较适用快慢双指针算法来进行解决。
快乐数
快乐数 - 力扣（LeetCode）https://leetcode.cn/problems/happy-number/description/
编写一个算法来判断一个数
n是不是快乐数。「快乐数」 定义为：
- 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1，那么这个数就是快乐数。
如果
n是 快乐数 就返回true；不是，则返回false。
请注意题目意义，只会有两种情况：
- 情况1：无限循环但始终变不到1
- 情况2：有限次数内，结果为1
所以对于这种循环往复的数据我们就可以联想到快慢双指针来做：
为了方便理解，我抽象的将数据做成链：
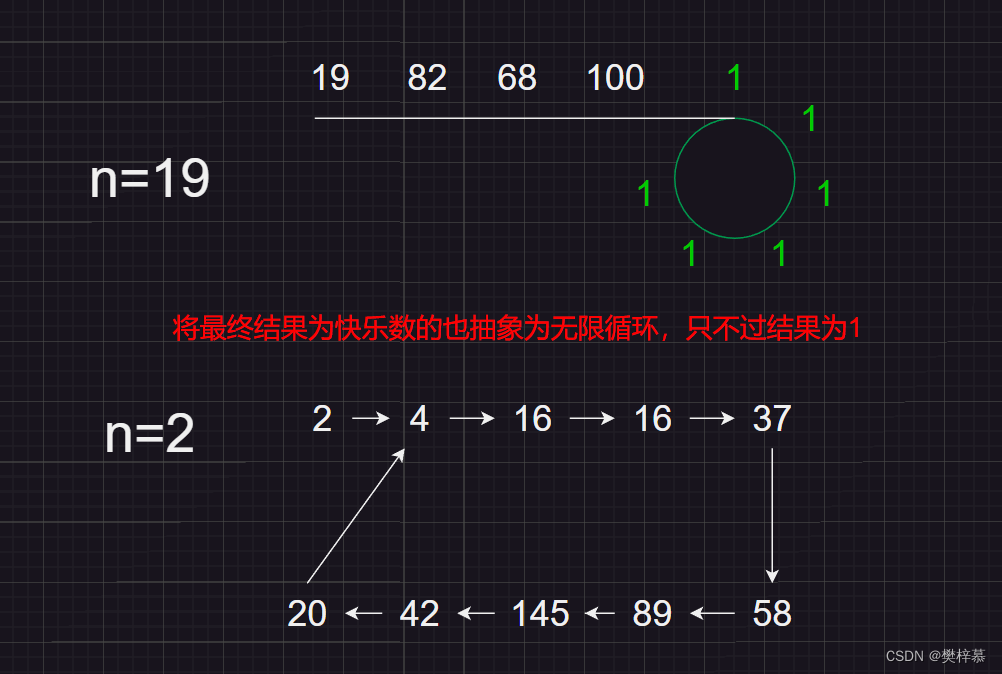
所以必然会成环，slow与fast必然会相遇，我们需要做的就是在他们相遇的时刻，检测以下slow或者fast的值是否为1即可。
有了思路，画图独立完成代码，不要直接看博主的代码。
class Solution {
public:int bitSum(int n) {int sum = 0;while (n) {int t = n % 10;sum += t * t;n /= 10;}return sum;}bool isHappy(int n) {int slow = n;int fast = bitSum(n);while (slow != fast) {slow = bitSum(slow);fast = bitSum(bitSum(fast));}return slow == 1;}
};3.对撞指针->暴力枚举的优化->利用单调性
一般用于顺序结构中，也称左右指针。
对撞指针从两端向中间移动。⼀个指针从最左端开始，另⼀个从最右端开始，然后逐渐往中间逼
近。
对撞指针的终止条件一般是两个指针相遇或者错开（也可能在循环内部找到结果直接跳出循
环），也就是：
- left == right（两个指针指向同⼀个位置）
- left > right（两个指针错开）
单调性解题的思路不好想到，但这是一种非常优秀的对暴力枚举方法的优化思想。
盛最多水的容器
盛最多水的容器 - 力扣（LeetCode）https://leetcode.cn/problems/container-with-most-water/description/
给定一个长度为
n的整数数组height。有n条垂线，第i条线的两个端点是(i, 0)和(i, height[i])。找出其中的两条线，使得它们与
x轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。
说明：你不能倾斜容器。
如果说利用暴力枚举的方式来做，很明显你需要固定一边，两层for循环解决，时间复杂度O(N^2)，但这道题目作为一道中等难度的题，利用暴力枚举必然会超时。
我们尝试利用对撞指针的方式来做：
w(宽)=right-left;
容积的计算公式：V=h*w
当计算完一组结果之后，我们需要将左指针或右指针向中间移动，这样如此反复就能得到最终答案，可是这样并没有降低时间复杂度，仍然是暴力枚举的思路。
我们观察：
当左指针或右指针向中间移动时w是必然减小的。
又根据木桶原理，h取决于左右指针指向的值小的那一个数据。
本题是依据数据分析，进而得到单调性的关系，需要大家自行画图分析，然后将思路转化成代码。
class Solution {
public:int maxArea(vector<int>& height) {int left=0;int right=height.size()-1;int v=0;int ret=0;while(left<right){int v=min(height[left],height[right])*(right-left);ret=max(v,ret);if(height[left]<height[right]) left++;else right--;}return ret;}
};有效三角形的个数
有效三角形的个数 - 力扣（LeetCode）https://leetcode.cn/problems/valid-triangle-number/description/
给定一个包含非负整数的数组
nums，返回其中可以组成三角形三条边的三元组个数。
构成三角形的条件：任意两边之和大于第三边
但这个条件转化成代码需要三次判断未免有些麻烦，所以我们可以将数组先进行排序，排序之后如果较小的两个值之和大于第三边，那么就可以构成三角形了。
暴力枚举的方式很显然时间复杂度O(N^3)。
那我们尝试着对数据进行分析，看看能否利用单调性来优化。
首先排序，我们将最大的数固定，然后利用对撞指针的思想进行优化。
有了思路，画图独立完成代码，不要直接看博主的代码。
class Solution {
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(),nums.end());int n=nums.size();int maxIndex=n-1;int ret=0;while(maxIndex>=2){int left=0;int right=maxIndex-1;while(left<right){if(nums[left]+nums[right]>nums[maxIndex]){ ret+=right-left;right--;}else{left++;}}maxIndex--;}return ret;}
};4.对撞指针->两数之和、三数之和、四数之和
两数之和
两数之和 - 力扣（LeetCode）https://leetcode.cn/problems/he-wei-sde-liang-ge-shu-zi-lcof/description/
购物车内的商品价格按照升序记录于数组
price。请在购物车中找到两个商品的价格总和刚好是target。若存在多种情况，返回任一结果即可。
首先我们发现数组是升序排列的，所以我们想到可以利用双指针来解决，同样的我们利用单调性，看看能否对暴力枚举的策略作优化。
暴力枚举的时间复杂度很明显O(N^2)。
两数之和大于target时，利用单调性，令right--即可；
两数之和小于target时，利用单调性，令left++即可；
两数之和等于target时，我们将此时的结果尾插到结果数组中。
class Solution {
public:vector<int> twoSum(vector<int>& price, int target) {int left=0;int right=price.size()-1;vector<int> ret;while(left<right){int sum=price[left]+price[right];if(sum<target) left++;else if(sum>target) right--;else{ret.push_back(price[left]);ret.push_back(price[right]);break;}}return ret;}
};三数之和
三数之和 - 力扣（LeetCode）https://leetcode.cn/problems/3sum/description/
给你一个整数数组
nums，判断是否存在三元组[nums[i], nums[j], nums[k]]满足i != j、i != k且j != k，同时还满足nums[i] + nums[j] + nums[k] == 0。请你返回所有和为
0且不重复的三元组。注意：答案中不可以包含重复的三元组。
本题可以借助两数之和的思想进行解题，无非就是需要多加一层循环，将第三个数固定即可。
另外的两个数仍然为两数之和的思想，只不过此时两数之和等于负的第三个数。
难点：注意本题要求去重，并且要求返回所有满足的数据，所以我们需要处理一些细节问题。
首先，关于返回所有：
- 当找到一种结果后，不能直接返回，要继续缩小区间继续寻找。
其次，关于去重：
- 找到一种结果之后，left和right要跳过重复元素。
- 当使用完一次双指针算法后，即更换第三个数时，也要跳过重复元素。
- 注意防止越界。
有了思路，画图独立完成代码，不要直接看博主的代码。
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {sort(nums.begin(), nums.end());vector<vector<int>> ret;int n = nums.size();for (int i = 0; i < n;){if (nums[i] > 0) break;//小优化int left = i + 1, right = n - 1, target = -nums[i];while (left < right){int sum = nums[left] + nums[right];if (sum < target) left++;else if (sum > target) right--;else{ret.push_back({ nums[left++],nums[right--],nums[i] });//去重 left 和 rightwhile (left < right && nums[left] == nums[left - 1]) left++;while (left < right && nums[right] == nums[right + 1]) right--;}}//去重 ii++;while (i < n && nums[i] == nums[i - 1]) i++;}return ret;}
};四数之和
四数之和 - 力扣（LeetCode）https://leetcode.cn/problems/4sum/description/
给你一个由
n个整数组成的数组nums，和一个目标值target。请你找出并返回满足下述全部条件且不重复的四元组[nums[a], nums[b], nums[c], nums[d]]（若两个四元组元素一一对应，则认为两个四元组重复）：
0 <= a, b, c, d < na、b、c和d互不相同nums[a] + nums[b] + nums[c] + nums[d] == target你可以按 任意顺序 返回答案 。
四数之和是三数之和的升级，本质上没有任何区别，只不过多加了一个需要固定的数，多加了一层循环而已，如果你已经掌握了三数之和，那么这道题对你来说会非常简单。
有了思路，画图独立完成代码，不要直接看博主的代码。
class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {sort(nums.begin(),nums.end());vector<vector<int>> ret;int n=nums.size();for(int i=0;i<n;){for(int j=i+1;j<n;){int left=j+1,right=n-1; long long num=(long long)target-nums[j]-nums[i];//需要注意的细节while(left<right){int sum=nums[left]+nums[right];if(sum>num) right--;else if(sum<num) left++;else{ret.push_back({nums[i],nums[j],nums[left++],nums[right--]});//去重 left 和 rightwhile(left<right && nums[left]==nums[left-1]) left++;while(left<right && nums[right]==nums[right+1]) right--;}}//去重 jj++;while(j<n && nums[j]==nums[j-1]) j++;}//去重ii++;while(i<n && nums[i]==nums[i-1]) i++;}return ret;}
};以上就是双指针算法在实际题目中的应用，总的来说，双指针算法是比较基础并且简单的算法。
大家只需要记住：当所给数据为有序时，不妨考虑用双指针算法进行解决。
🐸简单总结🐸
双指针擅于处理有序数据，可以解决数组分块、循环往复数据可以利用快慢指针思想（得到某个值可以理解为在某个值处循环）、对撞指针结合单调性可以优化暴力枚举（注意细节：去重和不漏）。
=========================================================================
如果你对该系列文章有兴趣的话，欢迎持续关注博主动态，博主会持续输出优质内容
🍎博主很需要大家的支持，你的支持是我创作的不竭动力🍎
🌟~ 点赞收藏＋关注 ~🌟
=========================================================================