当前位置：首页 > news >正文

seo网站案例河北百度seo

news 2025/8/12 8:11:14

seo网站案例,河北百度seo,不同网站对商家做o2o的政策,外贸门户网站斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”。对于解决此类问题方法有四，前两…

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”。对于解决此类问题方法有四，前两种对于初学者来说，应该可以思考研究明白，后两种就要求有一点点基础了，但是我相信，大家都可以学会的！！！

一、递归方法

完整代码展示如下：

#include <stdio.h>int fib(int n) 
{if (n <= 1) {return n;} else {return fib(n - 1) + fib(n - 2);}
}int main() 
{int n;printf("请输入一个整数： ");scanf("%d", &n);printf("斐波那契数列第%d项为： %d", n, fib(n));return 0;
}

递归方法实现原理如下：

首先检查输入的n是否小于等于1。如果是，那么直接返回n，因为斐波那契数列的前两项就是0和1。

如果n大于1，那么函数会递归地调用自身两次，分别传入n-1和n-2作为参数。这是因为斐波那契数列的定义是每一项都是前两项的和。

最后，将这两个递归调用的结果相加，并返回结果。

结果展示：

二、迭代方法

完整代码展示如下：

#include <stdio.h>int fib(int n) 
{if (n <= 1) {return n;}int a = 0, b = 1, temp;for (int i = 2; i <= n; i++) {temp = a + b;a = b;b = temp;}return b;
}int main() 
{int n;printf("请输入一个整数： ");scanf("%d", &n);printf("斐波那契数列的第%d项为： %d", n, fib(n));return 0;
}

迭代方法实现原理如下：

函数首先检查n是否小于等于1，如果是，则直接返回n。这是因为斐波那契数列的前两项是0和1。

如果n大于1，函数使用一个循环来计算斐波那契数列的第n项。在每次迭代中，它计算a和b的和，并将结果存储在临时变量temp中。然后，它将b的值赋给a，将temp的值赋给b。这样，a和b分别表示斐波那契数列的前两项和当前项。

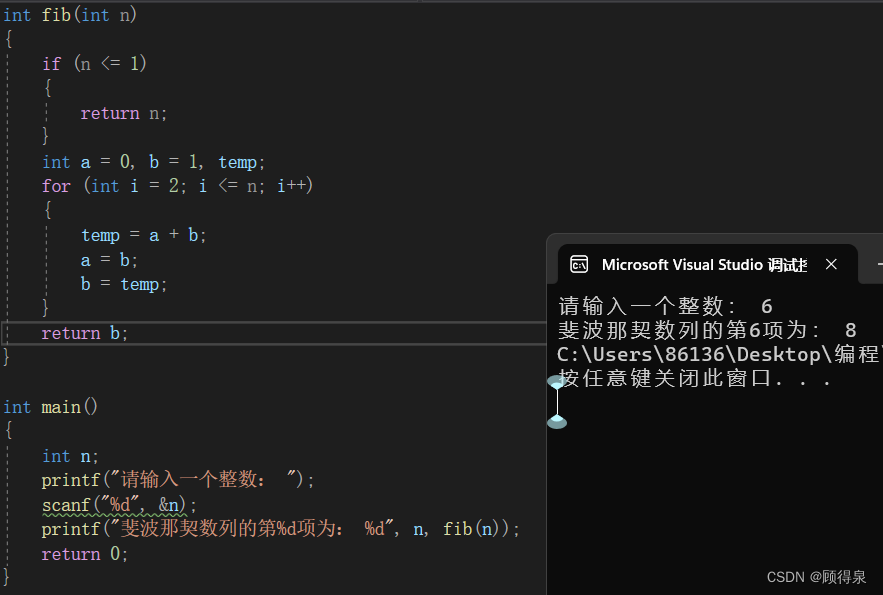
循环继续进行，直到i等于n。最后，函数返回b的值，即斐波那契数列的第n项。

结果展示：

三、数组方法

完整代码展示如下：

#include <stdio.h>void fib(int n) 
{int a[n];a[0] = 0;a[1] = 1;for (int i = 2; i < n; i++) {a[i] = a[i - 1] + a[i - 2];}for (int i = 0; i < n; i++) {printf("%d ", a[i]);}
}int main() 
{int n;printf("请输入斐波那契数列的长度： ");scanf("%d", &n);fib(n);return 0;
}

数组方法原理如下：

首先，代码声明了一个长度为n的整型数组a。然后，通过将数组的第一个元素和第二个元素分别赋值为0和1，初始化了斐波那契数列的前两个元素。

接着，使用一个for循环从索引2开始迭代到n-1。在每次迭代中，代码计算斐波那契数列的第i个元素，即前两个元素的和，并将其存储在数组a的相应位置。

最后，使用另一个for循环遍历数组a，并使用printf函数打印出每个元素的值。这样，你就可以看到斐波那契数列的前n个元素被打印出来了。

结果展示：

四、通项公式方法

要实现斐波那契数列通项公式方法，我们首先需要了解斐波那契数列的通项公式：

F(n) = (φ^n - (-φ)^-n) / sqrt(5)

其中，φ = (1 + sqrt(5)) / 2。

完整代码展示如下：

#include <stdio.h>
#include <math.h>double fibonacci(int n) 
{double phi = (1 + sqrt(5)) / 2;return (pow(phi, n) - pow(-phi, -n)) / sqrt(5);
}int main() 
{int n;printf("请输入要计算的斐波那契数列项数：");scanf("%d", &n);printf("第%d项斐波那契数列值为：%lf", n, fibonacci(n));return 0;
}

通项公式方法原理如下：

函数内部首先定义了一个变量phi，它的值为(1 + sqrt(5)) / 2，这是斐波那契数列中相邻两项之比的近似值。

接着，函数使用公式(pow(phi, n) - pow(-phi, -n)) / sqrt(5)来计算斐波那契数列的第n项。其中，pow(x, y)表示求x的y次方，sqrt(x)表示求x的平方根。

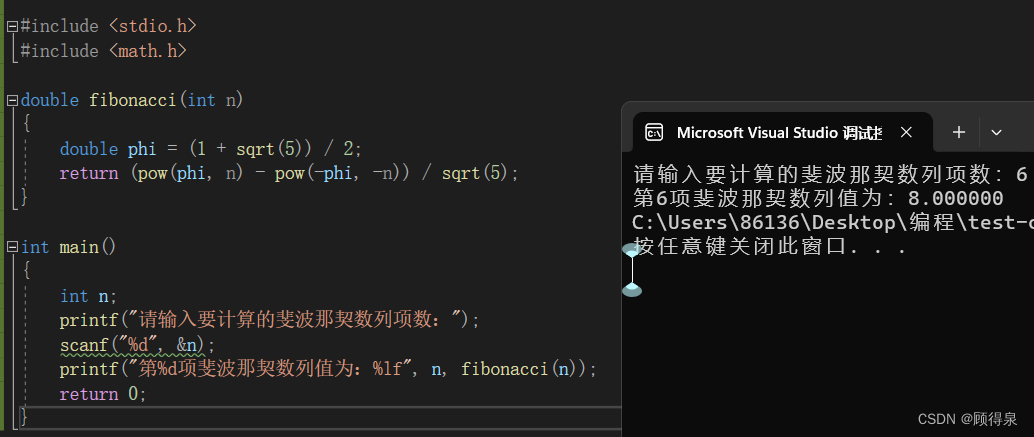
最后，函数返回计算得到的斐波那契数列第n项的值。

结果展示：