兰山网站建设竞价点击软件工具
😽PREFACE
🎁欢迎各位→点赞👍 + 收藏⭐ + 评论📝
📢系列专栏:算法
💪种一棵树最好是十年前其次是现在
1.什么是前缀和
前缀和指一个数组的某下标之前的所有数组元素的和(包含其自身)。前缀和分为一维前缀和,以及二维前缀和。前缀和是一种重要的预处理,能够降低算法的时间复杂度。可以快速地求出某一段的和。
2.一维前缀和
2.1 前缀和公式
已知数组:
前缀和:
2.2 前缀和的作用


而且前缀和时间复杂度:预处理O(n),查询O(1),效率比较高效,后续也会有一些其他的解法,比如说线段树,树状数组等,前缀和的运行时间是最短的。
【补】关于左端边界是1的选择
我们会发现求l到r的和时,用的是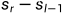 ,类似于数学里面的数列,此时令下标要l-1>=0,这就保证了
,类似于数学里面的数列,此时令下标要l-1>=0,这就保证了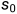 不需要定义任何的变量,使用起来比较简单
不需要定义任何的变量,使用起来比较简单
2.3 习题:前缀和

#include <iostream>
using namespace std;
const int N=1e5+10;
int n,m;
int a[N],s[N];
int main()
{scanf("%d %d",&n,&m);for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];//前缀和初始化while(m--){int l,r;scanf("%d %d",&l,&r);printf("%d\n",s[r]-s[l-1]);//区间和计算}return 0;}3.二维前缀和
3.1 二维前缀和公式
首先二维前缀和公式的成立是基于容斥定理的,二维前缀和实际上就是二维数组上的前缀和了。一维数组的前缀和也是一个一维数组,同样地,二维数组的前缀和也是一个二维的数组。

红色区域的和:
3.2 习题:子矩阵的和


这一子矩阵中的所有数之和为:
#include <iostream>
using namespace std;
const int N =1010;
int n,m,q;
int a[N][N],s[N][N];int main()
{scanf("%d %d %d",&n,&m,&q);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&a[i][j]);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];//求前缀和while(q--){int x1,y1,x2,y2;scanf("%d %d %d %d",&x1,&y1,&x2,&y2);printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);//算子矩阵的和}return 0;
}4.什么是差分
类似于数学中的求导和积分,差分可以看成前缀和的逆运算。

5.一维差分
5.1 习题:差分

a数组是b数组的前缀和数组,比如对b数组的b[i]的修改,会影响到a数组中从a[i]及往后的每一个数。
首先让差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c,,,,,, ,a[n] + c;
然后我们还需要补充,b[r+1] - c, a数组变成 a[r+1] - c,a[r+2] - c,,,,,,,,a[n] - c;
我们画个图理解一下这个公式的由来:

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int a[N], b[N];
int main()
{scanf("%d %d", &n, &m);for (int i = 1; i <= n; i++){scanf("%d", &a[i]);b[i] = a[i] - a[i - 1];//构建差分数组}int l, r, c;while (m--){scanf("%d %d %d", &l, &r, &c);b[l] += c;//将[l,r]之间的每个数都加上cb[r + 1] -= c;}for (int i = 1; i <= n; i++){a[i] = b[i] + a[i - 1];//前缀和运算printf("%d ", a[i]);}return 0;
}5.2 时间复杂度的分析
如果采用暴力方法,用for循环l到r区间,时间复杂度O(n),如果我们需要对原数组执行m次这样的操作,时间复杂度就会变成O(n*m)。考虑差分做法可极大地降低复杂度。给a数组中的[ l, r]区间中的每一个数都加上c,只需对差分数组b做 b[l] + = c, b[r+1] - = c。时间复杂度为O(1), 大大提高了效率。
6.二维差分
6.1 习题:差分矩阵

#include <iostream>
using namespace std;
const int N=1010;
int n,m,q;
int a[N][N],b[N][N];
int main()
{scanf("%d %d %d",&n,&m,&q);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];//同时求二维差分矩阵b,即将前缀和公式移项b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];}}while(q--){int x1,y1,x2,y2,c;cin>>x1>>y1>>x2>>y2>>c;//差分数组的模拟b[x1][y1]+=c;b[x1][y2+1]-=c;b[x2+1][y1]-=c;b[x2+1][y2+1]+=c;}//根据二维差分数组b去求二维前缀和矩阵afor(int i=1;i<=n;i++){for(int j=1;j<=m;j++){a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+b[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){printf("%d ",a[i][j]);}printf("\n");}return 0;}
6.2 差分矩阵的模拟
假定我们已经构造好了b数组,类比一维差分,我们执行以下操作来使被选中的子矩阵中的每个元素的值加上c:
b[x1][y1] + = c;
b[x1,][y2+1] - = c;
b[x2+1][y1] - = c;
b[x2+1][y2+1] + = c;每次对b数组执行以上操作,等价于:
for(int i=x1;i<=x2;i++)for(int j=y1;j<=y2;j++)a[i][j]+=c;图解过程:

b[x1][ y1 ] +=c ; //让整个a数组中矩形面积的元素都加上了c。
b[x1,][y2+1]-=c ; //让整个a数组中绿色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2+1][y1]- =c ; //让整个a数组中紫色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2+1][y2+1]+=c; //让整个a数组中红色矩形面积的元素再加上c,红色内的相当于被减了两次,再加上一次c,才能使其恢复。



