记事本网站开发百度关键词优化系统
文章目录
- Day57
- 回文子串
- 题目
- 思路
- 代码
- 最长回文子序列
- 题目
- 思路
- 代码
Day57
回文子串
647. 回文子串 - 力扣(LeetCode)
题目
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
思路
动规五部曲
- 确定dp数组以及下标含义
本题如果我们定义,dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话,我们会发现很难找到递归关系。
dp[i] 和 dp[i-1] ,dp[i + 1] 看上去都没啥关系。
所以我们要看回文串的性质。 如图:
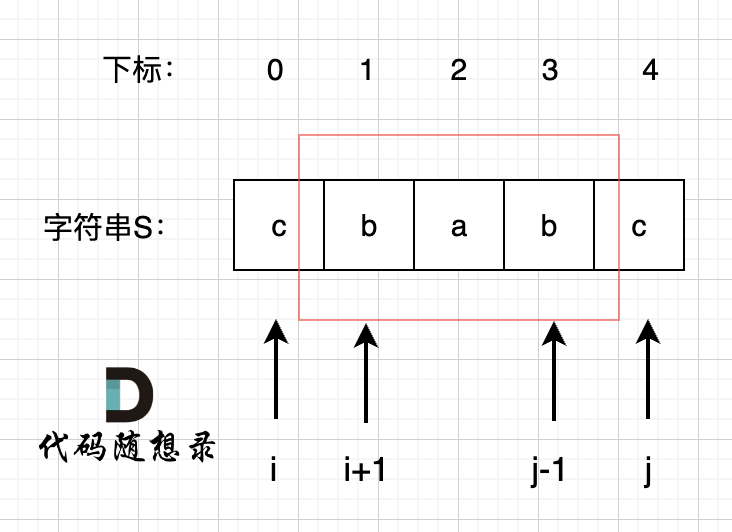
我们在判断字符串S是否是回文,那么如果我们知道 s[1],s[2],s[3] 这个子串是回文的,那么只需要比较 s[0]和s[4]这两个元素是否相同,如果相同的话,这个字符串s 就是回文串。
那么此时我们是不是能找到一种递归关系,也就是判断一个子字符串(字符串的下表范围[i,j])是否回文,依赖于,子字符串(下表范围[i + 1, j - 1])) 是否是回文。
所以为了明确这种递归关系,我们的dp数组是要定义成一位二维dp数组。
布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
- 确定递推公式
在确定递推公式时,就要分析如下几种情况。
整体上是两种,就是s[i]与s[j]相等,s[i]与s[j]不相等这两种。
当s[i]与s[j]不相等,那没啥好说的了,dp[i][j]一定是false。
当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况
-
情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
-
情况二:下标i 与 j相差为1,例如aa,也是回文子串
-
情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
if(s.charAt(i) == s.charAt(j)){
if (j - i <= 1){ // 情况一, 情况二
count++;
dp[i][j] = true;
}else if(dp[i + 1][j - 1]){ // 情况三
count++;
dp[i][j] = true;
}
}
result就是统计回文子串的数量。
注意这里我没有列出当s[i]与s[j]不相等的时候,因为在下面dp[i][j]初始化的时候,就初始为false。
- dp数组初始化
dp[i][j]初始化为false。
- 遍历顺序
首先从递推公式中可以看出,情况三是根据dp[i + 1][j - 1]是否为true,在对dp[i][j]进行赋值true的。
dp[i + 1][j - 1] 在 dp[i][j]的左下角,如图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Wis0JIQb-1691292330556)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210121171032473-20230310132134822.jpg “647.回文子串”)]
如果这矩阵是从上到下,从左到右遍历,那么会用到没有计算过的dp[i + 1][j - 1],也就是根据不确定是不是回文的区间[i+1,j-1],来判断了[i,j]是不是回文,那结果一定是不对的。
所以一定要从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的。
有的代码实现是优先遍历列,然后遍历行,其实也是一个道理,都是为了保证dp[i + 1][j - 1]都是经过计算的。
for(int i = sLen - 1; i >= 0; i--){for(int j = i; j < sLen; j++){if(s.charAt(i) == s.charAt(j)){if (j - i <= 1){ // 情况一, 情况二count++;dp[i][j] = true;}else if(dp[i + 1][j - 1]){ // 情况三count++;dp[i][j] = true;}}}
}
- 举例递推公式
举例,输入:“aaa”,dp[i][j]状态如下:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FfEMQWFb-1691292330556)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210121171059951-20230310132153163.jpg “647.回文子串1”)]
图中有6个true,所以就是有6个回文子串。
注意因为dp[i][j]的定义,所以j一定是大于等于i的,那么在填充dp[i][j]的时候一定是只填充右上半部分。
代码
class Solution {public int countSubstrings(String s) {int sLen = s.length();int count = 0;boolean dp[][] = new boolean[sLen][sLen];for(int i = sLen - 1; i >= 0; i--){for(int j = i; j < sLen; j++){/**整体上是两种,就是s[i]与s[j]相等,s[i]与s[j]不相等这两种。当s[i]与s[j]不相等,dp[i][j]一定是false。当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串情况二:下标i 与 j相差为1,例如aa,也是回文子串情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。*/if(s.charAt(i) == s.charAt(j)){if (j - i <= 1){ // 情况一, 情况二count++;dp[i][j] = true;}else if(dp[i + 1][j - 1]){ // 情况三count++;dp[i][j] = true;}}}}return count;}
}
最长回文子序列
516. 最长回文子序列 - 力扣(LeetCode)
题目
给定一个字符串 s ,找到其中最长的回文子序列,并返回该序列的长度。可以假设 s 的最大长度为 1000 。
示例 1: 输入: “bbbab” 输出: 4 一个可能的最长回文子序列为 “bbbb”。
示例 2: 输入:“cbbd” 输出: 2 一个可能的最长回文子序列为 “bb”。
提示:
- 1 <= s.length <= 1000
- s 只包含小写英文字母
思路
回文子串是要连续的,回文子序列可不是连续的! 回文子串,回文子序列都是动态规划经典题目。
动规五部曲分析
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
- 确定递推公式
在判断回文子串的题目中,关键逻辑就是看s[i]与s[j]是否相同。
如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;
如图: [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sCwR202k-1691292330556)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210127151350563.jpg “516.最长回文子序列”)]
(如果这里看不懂,回忆一下dp[i][j]的定义)
如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为dp[i][j - 1]。
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-znfAuWDQ-1691292330557)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210127151420476.jpg “516.最长回文子序列1”)]
if(s.charAt(i) == s.charAt(j)){dp[i][j] = dp[i + 1][j - 1] + 2;
}else{dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
- dp数组如何初始化
首先要考虑当i 和j 相同的情况,从递推公式:dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况。
所以需要手动初始化一下,当i与j相同,那么dp[i][j]一定是等于1的,即:一个字符的回文子序列长度就是1。
其他情况dp[i][j]初始为0就行,这样递推公式:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); 中dp[i][j]才不会被初始值覆盖。
- 确定遍历顺序
从递归公式中,可以看出,dp[i][j] 依赖于 dp[i + 1][j - 1] ,dp[i + 1][j] 和 dp[i][j - 1],如图:
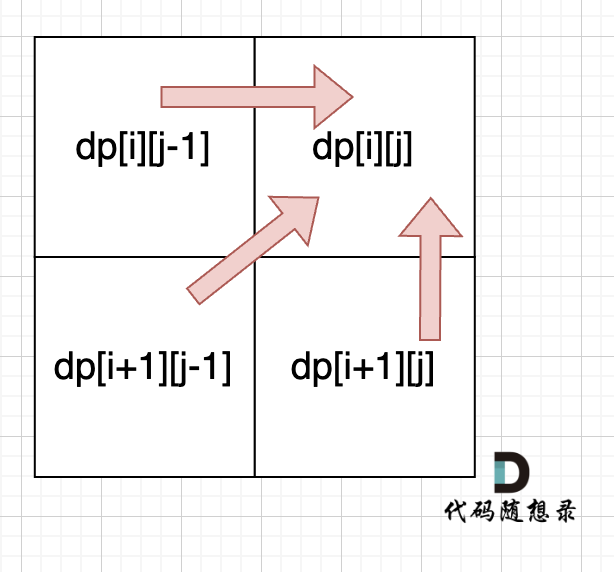
所以遍历i的时候一定要从下到上遍历,这样才能保证下一行的数据是经过计算的。
j的话,可以正常从左向右遍历。
for(int i = sLen - 1; i >= 0; i--){for(int j = i + 1; j < sLen; j++){if(s.charAt(i) == s.charAt(j)){dp[i][j] = dp[i + 1][j - 1] + 2;}else{dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);}}
}
- 举例推导dp数组(一定要推导)
输入s:“cbbd” 为例,dp数组状态如图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wh0U0pFO-1691292330557)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210127151521432.jpg “516.最长回文子序列3”)]
红色框即:dp[0][s.size() - 1]; 为最终结果。
代码
class Solution {public int longestPalindromeSubseq(String s) {int sLen = s.length();// dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。int dp[][] = new int[sLen][sLen];for(int i = 0; i < sLen; i++) dp[i][i] = 1;for(int i = sLen - 1; i >= 0; i--){for(int j = i + 1; j < sLen; j++){if(s.charAt(i) == s.charAt(j)){dp[i][j] = dp[i + 1][j - 1] + 2;}else{dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);}}}return dp[0][sLen - 1];}
}
