漳州做网站公司宝鸡seo排名
引入
- 冒泡排序顾名思义,就是像冒泡一样,泡泡在水里慢慢升上来,由小变大。
- 虽然冒泡排序和冒泡并不完全一样,但却可以帮助我们理解冒泡排序。
思路
- 一组无序的数组,要求我们从小到大排列
- 我们可以先将最大的元素放在数组末尾
- 再将第二大的数放在数组的倒数第二个位置
- 再将第三大的数放在数组的倒数第三个位置
- 以此类推
- 那么现在问题的关键就是如何将 第 n 大的数 放在 倒数第 n 个位置 ---> 交换
- 下面是冒泡排序的gif动画,该图来自于菜鸟教程
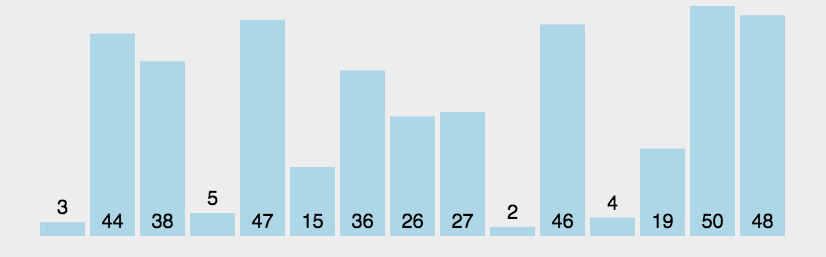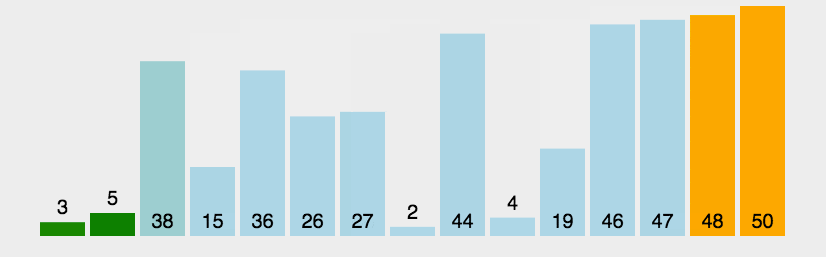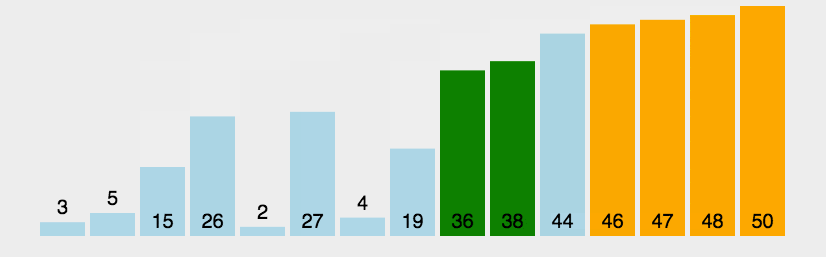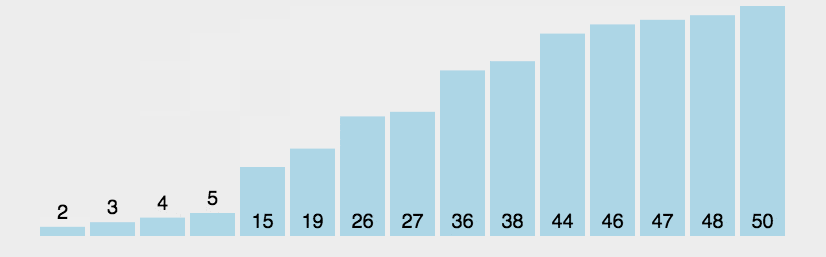
实现
提醒
- 现在我们假设无序数组长度为 n 即下标 [ 0 , n-1 ]
- 当前元素下标为 i ,下一个元素的下标为 j
第一次遍历 [ 0 , n - 1- 1 ] ---> [ 0 , n -2 ]
- 如果 当前元素 > 后一个元素 ,那么就交换两个元素 , 再进行下次遍历
- 如果 当前元素 > 后一个元素 , 直接进行下次遍历
- 直到遍历完成之后,最大的值就在一次一次的交换中被交换到了数组末尾
- 思考:为什么是从 0 开始遍历 ,n-2 结束 ?
- 因为 j 为 i 的下一个元素下标 ,如果为 [ 0,n-1 ]的话 ,那么当前元素下标就可以为 n - 1,那么下一个元素的下标就为 n ,显然数组下标越界了
- 而且正因为是从 [ 0 , n -2] 范围遍历 ,刚好可以保证经过这一轮遍历后 ,最大的数在数组末尾 ( i = n - 2 【即为倒数第二个数】 ,j = i + 1【末尾数】)
第二次遍历 [ 0 , n - 1- 2]----> [ 0 , n -3 ]
- 经过第一次遍历,我们已经将最大的数移动到了数组末尾,所以,我们不用在去对末尾以确定的数进行比较,我们可以减少次数,来提高效率
- 再次引用第一次遍历的步骤
......
最后一次遍历 [ 0 , n - 1 - (n-1) ] ---- > [ 0 , 0 ]
- 最后一次遍历的情况就是还剩下两个元素未进行排序的情况 ,即下标 0 和 下标 1 未进行排序
- 只需对这两个元素进行排序后,就完成了这个数组的排序
怎么确定一共需要遍历几次及每次遍历的数组下标范围
- 遍历次数问题
- 我们先来做一个假设
- 如果一个数组只有两个元素,那么应该遍历几次 ? 1 次
- 如果一个数组只有三个元素,那么应该遍历几次 ? 2次
- 第一次将最大的数放在最末尾 ,第二次将第二大的数放在倒数第二 , 第三大的元素自然而然就在倒数第三了【即第一个】 ,不用遍历
- 如果一个数组只有四个元素,那么应该遍历几次 ? 3 次
- 第一次将最大的数放在最末尾 ,第二次将第二大的数放在倒数第二 , 第三次将第三大的元素放在在倒数第三 ,剩下一个元素,不用排
- 显而易见,如果有 n 个 元素 ,那么就需要遍历 n - 1 次
- 每次遍历数组下标
- 按照上面的实现部分
- 第一次遍历我们需要数组的下标为 [ 0 , n -2 ]
- 第二次遍历我们需要数组的下标为 [ 0 , n -3 ]
- 第三次遍历我们需要数组的下标为 [ 0 , n -4 ]
- 那么就有一个规律了 ,n - 2 , n - 3 , n - 4
- 当我们正在进行第一次遍历时,用一个变量保存 m = 1 , 那么第一次遍历下标可以为 [ 0 , n -1 - m ]
- 当我们正在进行第二次遍历时,用一个变量保存 m = 2 , 那么第一次遍历下标可以为 [ 0 , n -1 - m ]
- 当我们正在进行第三次遍历时,用一个变量保存 m = 3 , 那么第一次遍历下标可以为 [ 0 , n -1 - m ]
- 当我们正在进行最后一次遍历时,用一个变量保存 m = n - 1, 那么第一次遍历下标可以为 [ 0 , n -1 - m ] ---> [ 0 , n - 1 - (n -1) ]
代码实现
// 冒泡排序算法
public static int[] bubble(int[] ints){// 注意我这里使用的是 < , 而不是我思路中的 <= , 可以自行更改 ,如果没想明白说明你还没有理解// 用 i 来表示一共需要遍历多少次for (int i = 0; i < ints.length-1; i++) {// 真正开始进行遍历 ,根据 i 的值 不同 ,j 就不同 ,也就是说每次大遍历中小遍历的次数不同for (int j = 0; j < ints.length-1-i; j++) {// 如果前一个元素 > 后一个元素 ,则交换if (ints[j] > ints[j+1]){int temp = ints[j];ints[j] = ints[j+1];ints[j+1] = temp;}// 继续下次遍历}}return ints;
}
