wordpress4.9+多站点三叶草gw9356

欧拉函数

互质就是两个数的最大公因数只有1，体现到代码里面就是a和b互质，则b mod a = 1 mod a (目前我不是很理解，但是可以这样理解：a和b的最大公因数是1，即1作为除数和b作为除数时，对于被除数a来说余数是一样的，即1/a的余数和b/a是一样的，即b mod a = 1 mod a)
欧拉函数的作用是求1-n与n互质的个数

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
#include <unordered_map>
using namespace std;void get_eura(int x)
{int res = x;for (int i = 2; i <= x / i; ++ i){if (x % i == 0){//res = res * (1 - 1/i);或者res = res * (i - 1) / i;都不行，前者是浮点数1 后者会溢出res = res / i * (i - 1);while (x % i == 0){x /= i;}}}if (x > 1) res = res / x * (x - 1);cout << res << endl;
}
void solve()
{int n;cin >> n;while (n -- ){int x;cin >> x;get_eura(x);}
}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;//cin >> T;while (T --) solve();return 0;
}

AcWing 874. 筛法求欧拉函数

线性筛 + 欧拉函数（有一点推公式）

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
#include <unordered_map>
using namespace std;
const int N = 1e6 + 10;
int primes[N], st[N], eulers[N];
int cnt;
void get_eulers(int x)
{eulers[1] = 1;  for (int i = 2; i <= x; ++ i)//只是在线性筛的过程中顺便求了一下每个数的欧拉函数{if (!st[i])//1-n的质数{primes[cnt++] = i;eulers[i] = i - 1;}for (int j = 0; primes[j] <= x / i; ++ j)//1-n的合数//任何合数都含有质因数，4 = 1 * 2 * 1 * 2；{st[primes[j] * i] = 1;if (i % primes[j] == 0){eulers[i * primes[j]] = eulers[i] * primes[j];break;//其实也相当于一个else}//eulers[i * primes[j]] = eulers[i] * primes[j] / primes[j] * (primes[j] - 1);eulers[i * primes[j]] = eulers[i] * (primes[j] - 1);}}
}
void solve()
{int n;cin >> n;get_eulers(n);long long res = 0; for (int i = 1; i <= n; ++ i) res += eulers[i];cout << res;
}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;//cin >> T;while (T --) solve();return 0;
}

快速幂

1 2 4 8成指数倍增长 log的时间复杂度

AcWing 875. 快速幂

long long qmi(int a, int b, int p)
{long long res = 1;while (b){if (b & 1){res = res * a % p;}a = a * (long long)a % p;b >>= 1;}return res;
}

AcWing 876. 快速幂求逆元

欧拉函数 =>费马定理 =>快速幂实现费马定理计算结果

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
#include <unordered_map>
using namespace std;long long qmi(int a, int b, int p)
{long long res = 1;while (b){if (b & 1) res = res * a % p;a = (long long)a * a % p;b >>= 1;}return res;
}
void solve()
{int n;cin >> n;while (n --){int a, p;cin >> a >> p;if (a % p == 0) cout << "impossible" << endl;else cout << qmi(a, p - 2, p) << endl;//a需要与m互质，否则a不存在乘法逆元}
}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;//cin >> T;while (T --) solve();return 0;
}

扩展欧几里德（裴蜀定理）

AcWing 877. 扩展欧几里得算法

理解递归的本质：

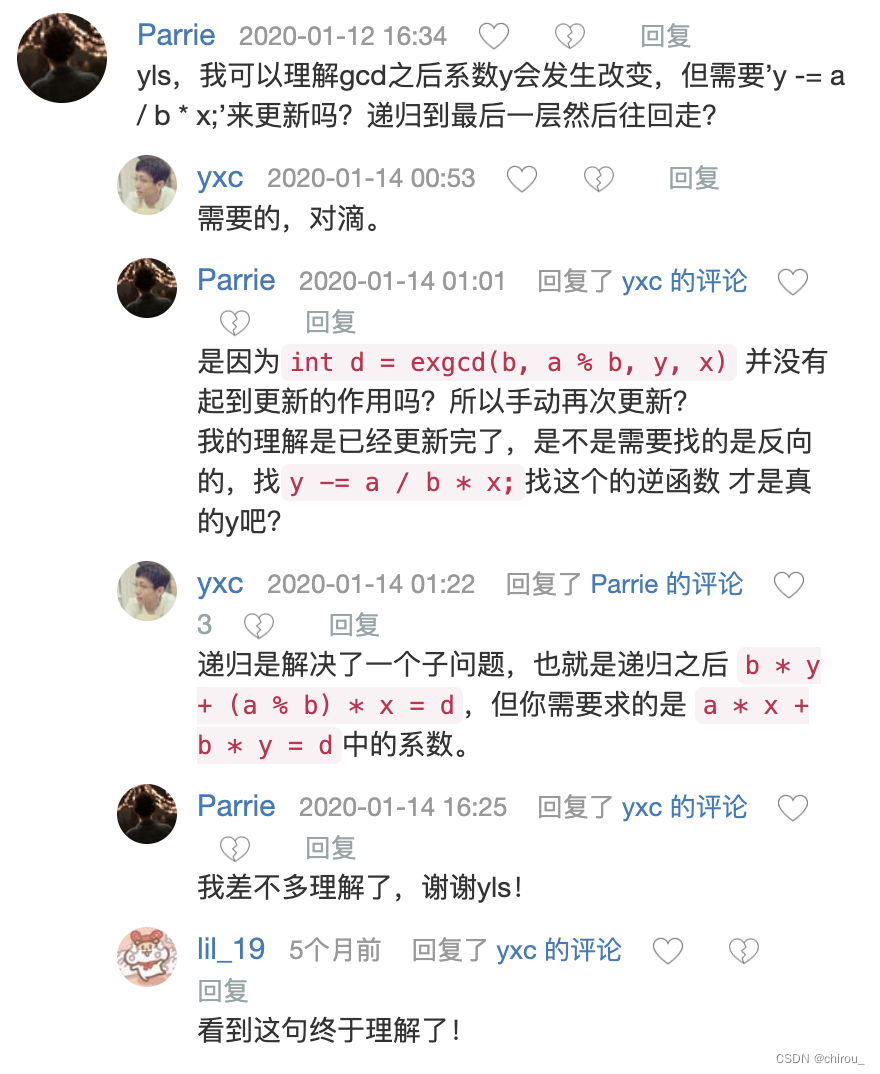
裴蜀定理和线性同余方程的证明：

#include <cstdio>
#include <iostream>using namespace std;int exgcd(int a, int b, int &x, int &y)
{if (b == 0){x = 1, y = 0;return a;}//d就是最大公约数，本题其实用不到int d = exgcd(b, a % b, y, x);//本题的精髓/*只是为了方便更改x和y的值，如果用d = exgcd(b, a % b, x, y);最后就解得 新x = y 新y = x - a / b * y那么代码就得这么写int t = y;y = x - a / b * y;x = t;显然比只要写一句 新y -= a / b * x; 麻烦*/y -= a / b * x;return d;
}
void solve()
{int n;cin >> n;while (n -- ){int a, b, x, y;cin >> a >> b;exgcd(a, b, x, y);cout << x << " " << y << endl;}
}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;//cin >> T;while (T --) solve();return 0;
}

AcWing 878. 线性同余方程

线性同余方程用扩展欧几里德定理求解
本题推导过程在上面
为什么要% m

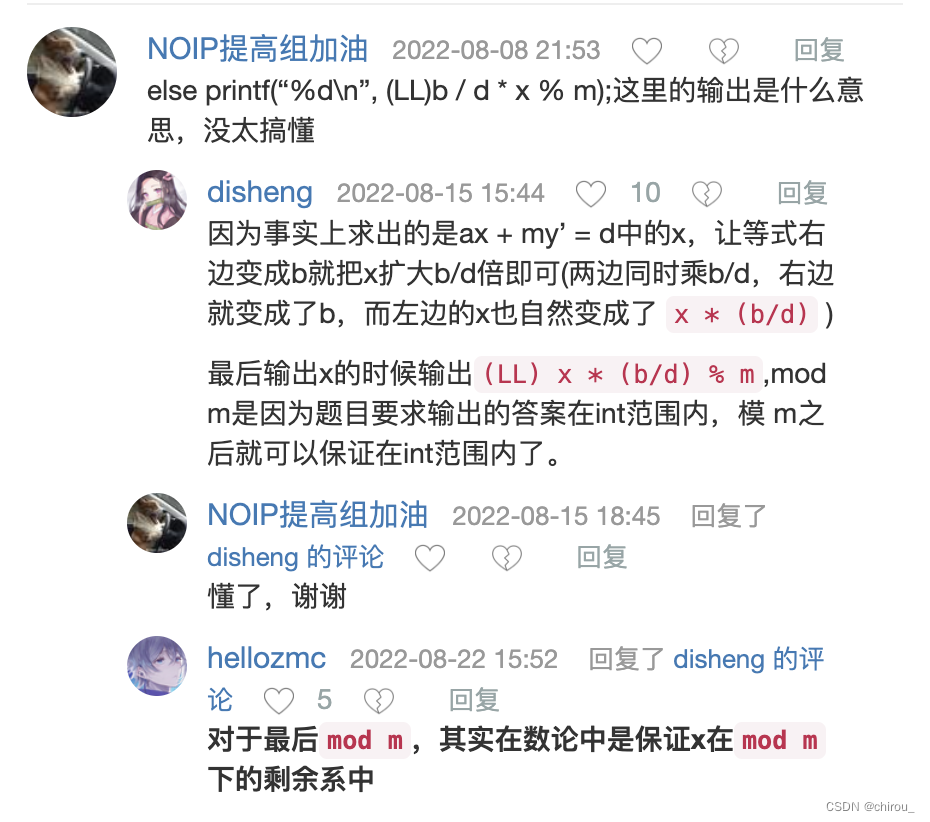
#include <cstdio>
#include <iostream>using namespace std;int exgcd(int a, int b, int &x, int &y)
{if (b == 0){x = 1, y = 0;return a;}else//其实不用else，上面满足直接return了，上面不满足也会走到下面 {int d = exgcd(b, a % b, y, x);y -= a / b * x;return d;}
}
void solve()
{int n;cin >> n;while (n -- ){int a, b, m, x, y;cin >> a >> b >> m;int d = exgcd(a, -m, x, y);if (b % d != 0) cout << "impossible" << endl;else cout << (long long)b / d * x % m << endl;}
}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;//cin >> T;while (T --) solve();return 0;
}

中国剩余定理