广告设计网站素材如何在网络上推广产品

abstract

• 讨论$\sin ,\cos ,\tan$的图象性质,这些性质可以借助单位圆分析
  • $y=\cos x$:余弦曲线
  • $y=\sin x$:正弦曲线
  • $y=\tan x$:正切曲线

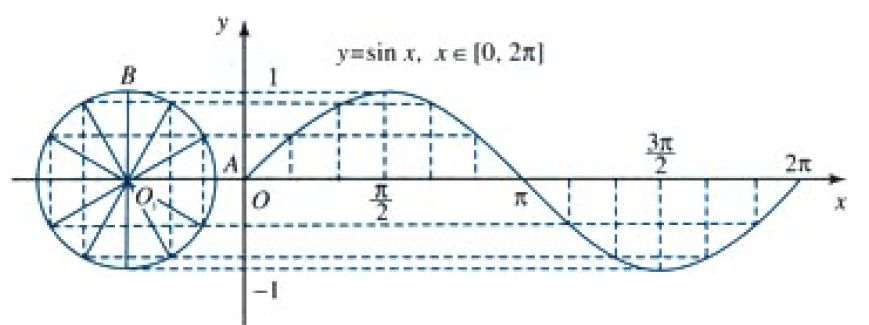	正弦线和正弦曲线
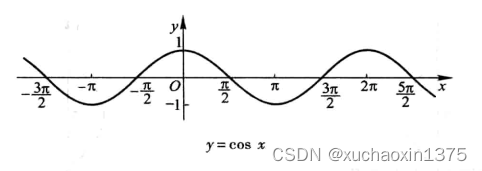	余弦曲线
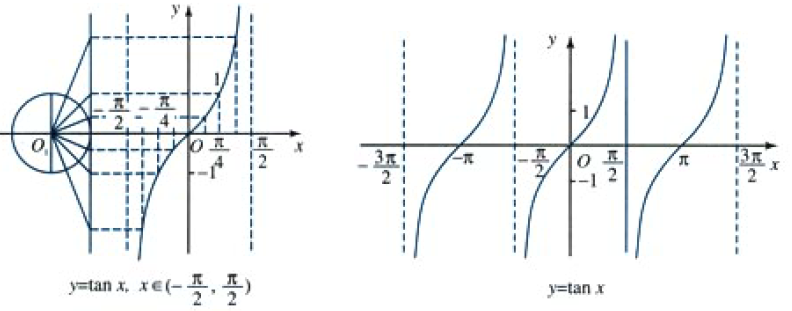	正切线和正切曲线

正弦函数

• $y=\sin x$,$x\in \mathbb{R}$是正弦函数,其中自变量$x$是弧度值
  • 定义域:$\mathbb{R}$
  • 值域:$[-1,1]$
    • 当$x=-\frac{\pi }{2}+2k\pi$,$k\in \mathbb{Z}$时取得最小值$-1$
    • 当$x=\frac{\pi }{2}+2k\pi$,$k\in \mathbb{Z}$时取得最大值1
  • 有界性:$|\sin x|⩽1$
  • 奇偶性:奇函数
  • 周期性:最小正周期为$2\pi$
  • 单调性:$[-\frac{\pi }{2}+2k\pi ,\frac{\pi }{2}+2k\pi ]$为递增区间;$[\frac{\pi }{2}+2k\pi ,\frac{3\pi }{2}+2k\pi ]$为递减区间;$k\in \mathbb{Z}$
• 正弦函数刻画的是弧度$x$对应的正弦值$\sin x$

正弦型函数

• $y=A\sin (\omega x+\varphi )$,称为正弦型函数
• 相比于正弦函数$y=\sin x$,$y=A\sin (\omega x+\varphi )$增加了两个影响函数的参数$A,\omega ,\varphi$(它们不是变量,而都是常数)
• 这个函数在物理应用中很常见,具有明显的物理意义
• 正弦型函数和仍可以用圆周运动来描述:
  • 设直角坐标系中某点$P(x,y)$绕着原点$O$以半径为$R$的圆轨迹作角速度为$\omega$ rad/s的圆周运动
  • 设旋转前$P$的位置为$P_0$,且$OP$是$\varphi$的终边
  • 经过$t$秒后,点$P$来到了新位置,且$OP$是$\varphi +\omega t$的终边
  • 容易算得$P$的坐标$(x,y)$关于时间$t$的函数关系
    • $x=R\cos (\omega t+\varphi )$
    • $y=R\sin (\omega t+\varphi )$
    • 推导方式如下:
      • 在直角坐标系$xOy$上,令角$\varphi$的顶点为$O$坐标原点重合,$\varphi$的始边与$x$轴正半轴重合
      • 并以$O$为圆心构造单位圆,$\varphi$与单位圆的交点的坐标为$E(\cos \varphi ,\sin \varphi )$
      • 而$P_0$也是$\varphi$终边上的点,且$O{P}_0=R$;则$P_0$的坐标$(P_{0x},P_{0y})$是$E$的坐标$(\sin \alpha ,\cos \alpha )$的$R$倍:$P_{0x}=R\cos \varphi$,$P_{0y}=R\sin \varphi$
      • 对于终边$\omega t+\varphi$上的$P$点坐标为$(R\cos (\omega t+\varphi ),R\sin (\omega t+\varphi ))$
  • 这就得到了正弦型函数$y=A\sin (\omega x+\varphi )$

转动相关概念

旋转角速度

• 坐标系内的点$P(x,y)$绕点$O$在单位时间内旋转过的角的弧度数$\omega$

转动周期

• $y=R\sin (\omega t+\varphi )$中,点$P$旋转一周所需要的时间为$T=\frac{2\pi }{\omega }$,这个时间也称为转动周期

  • 令$\alpha =\omega t+\varphi$,设函数$y$的最小正周期为$T_0$,则$y(t+T_0)$=$y(t)$
  • 即$R\sin (\omega (t+T_0)+\varphi )$=$R\sin (\omega t+\varphi )$,即$\sin ((\omega t+\varphi )+\omega T_0)$=$\sin (\omega t+\varphi )$
  • 所以$\sin (\alpha +T_0)=\sin (\alpha )$
  • $\sin \alpha$的周期为$2\pi$,那么$\omega T_0$=$2\pi$,所以$T_0=\frac{2\pi }{\omega }$

• 此外,还可以从坐标的伸缩角度来得到转动周期计算公式

• 例:$\sin (kx)$,$k=1,2,3,\cdots ,n$时,在$[0,2\pi ]$内取得最大值1的极值点(满足$kx=\frac{\pi }{2}$)分别是:$\frac{\pi }{2}$,$\frac{\pi }{4}$,$\frac{\pi }{6}$,$\cdots$,$\frac{\pi }{2n}$

转动频率

• 一秒内,点$P$旋转的周数$f=\frac{1}{T}$=$\frac{\omega }{2\pi }$,称为转动的频率

初相

• 角$\varphi$也叫做初相

小结

• 转动周期(转动频率)只和$\omega$相关,而与$\varphi$无关
• $\omega$越大,在一定区间内曲线波动的次数就越多,反之越少

余弦函数的图象与性质

• 我们可以通过诱导公式$y=\sin (\frac{\pi }{2}+x)$=$\cos x$得知,$y=\cos x$的图象和$\sin (\frac{\pi }{2}+x)$的图象相同
• 所以可以通过研究正弦型函数来研究余弦函数(正弦函数向左平移2个单位就可以得到余弦函数的图象)
• 此外,余弦型函数$y=A\cos (\omega x+\varphi )$可以转换为$y=A\sin (\omega x+\varphi +\frac{\pi }{2})$

性质

• 定义域和值域和周期同正弦函数
  • 当且仅当$x=\pi +2k\pi$,$k\in \mathbb{Z}$时,取得最小值$-1$
  • 当且仅当$x=2k\pi$,$k\in \mathbb{Z}$时,余弦函数取值得最大值1
• 奇偶性:偶函数
• 单调性:$[2k\pi ,\pi +2k\pi ]$,$k\in \mathbb{Z}$时函数单调递减;$[\pi +2k\pi ,2\pi +2k\pi ]$,$k\in \mathbb{Z}$函数单调递增

正切函数的图象和性质

• 定义域: { x ∣ x ≠ k π + π 2 , k ∈ Z } \set{x|x\neq{k\pi+\frac{\pi}{2}},k\in\mathbb{Z}} {x∣x=kπ+2π​,k∈Z},
• 值域:$\mathbb{R}$
  • 在区间$(-\frac{\pi }{2},\frac{\pi }{2})$内,当$x<\frac{\pi }{2}$且无限接近$\frac{\pi }{2}$时,$\tan x$趋于无限大,记为$\tan x\to +\infty$
  • 另一侧有$x\to -\frac{\pi }{2}$时 $\tan x\to -\infty$
• 周期:$\pi$
  • 由$\tan (\pi +x)$=$\tan x$,所以$\pi$是$\tan x$的一个周期
  • 并且结合单位圆中的正弦线,容易说明最小正周期为$\pi$
• 奇偶性:奇函数
• 单调性:$(-\frac{\pi }{2}+k\pi ,\frac{\pi }{2}+k\pi )$,$k\in \mathbb{Z}$区间内函数单调增加

由已知三角函数值求角

任意角范围内

• 通常可以用单位圆来求解具有给定三角函数值对应的弧度角
• 例如:已知$\sin x=\frac{\sqrt{2}}{2}$,求
  • $x$的可能取值
  • $x\in [-\frac{\pi }{2},\frac{\pi }{2}]$条件下$x$的取值
• 解:
  • 由单位圆可知,$\frac{\pi }{4}+2k\pi$,$(\pi -\frac{\pi }{4})+2k\pi$,$(k\in \mathbb{Z})$都满足$\sin x=\frac{\sqrt{2}}{2}$,
    • 用集合表示为: { x ∣ x = 2 k π + π 4 ( k ∈ Z ) } \set{x|x=2k\pi+\frac{\pi}{4}(k\in{\mathbb{Z}})} {x∣x=2kπ+4π​(k∈Z)} $\bigcup$ { x ∣ x = 2 k π + 3 π 4 ( k ∈ Z ) } \set{x|x=2k\pi+\frac{3\pi}{4}(k\in\mathbb{Z})} {x∣x=2kπ+43π​(k∈Z)}
  • 若$x\in [-\frac{\pi }{2},\frac{\pi }{2}]$,由单位圆可知,$x=\frac{\pi }{4}$

反三角函数(限定范围内)

• 已知三角函数值求角的过程的所建立的函数称为反三角函数
• 由于单射函数才有反函数,反三角函数根据限定三角函数内的一段单调区间定义出来

反正弦

• 一般地,对于正弦函数$y=\sin x$,若已知函数值为$y(y\in [-1,1])$,那么$[-\frac{\pi }{2},\frac{\pi }{2}]$上由唯一的$x$值和它对应,记为$x=\arcsin y$,(其中$-1⩽y⩽1$,$-\frac{\pi }{2}⩽x⩽\frac{\pi }{2}$)
• 例如:$\sin x=\frac{1}{2}$,$x\in [-\frac{\pi }{2},\frac{\pi }{2}]$,求$x$的问题可以表示为$\arcsin \frac{1}{2}$

反余弦

• 在区间$[0,\pi ]$上符合条件$\cos x=y$,$(y\in [-1,1])$的求角$x$,记为$x=\arccos y$
• 例
  1. $\arccos \frac{1}{2}=\frac{\pi }{3}$
  2. 已知$\cos x=-\frac{\sqrt{2}}{2}$,且$x\in [0,2\pi ]$,求$x$的取值集合
     • 由单位圆可知,解集为 { 3 π 4 , 5 π 4 } \set{\frac{3\pi}{4},\frac{5\pi}{4}} {43π​,45π​}
     • 用反余弦函数表示: { arccos ⁡ ( − 2 2 ) , π + arccos ⁡ 2 2 } \set{\arccos{(-\frac{\sqrt{2}}{2})},\pi+\arccos\frac{\sqrt{2}}{2}} {arccos(−22 ​​),π+arccos22 ​​}

反正切

• 一般地,若$\tan x=y(y\in \mathbb{R})$,且$x\in (-\frac{\pi }{2},\frac{\pi }{2})$,那么对每一个正切值$y$,在开区间$(-\frac{\pi }{2},\frac{\pi }{2})$内,有且只有一个角$x$满足$\tan x=y$,记为$x=\arctan y$,$x\in (-\frac{\pi }{2},\frac{\pi }{2})$
• 例如$\arctan \frac{\sqrt{3}}{3}$=$\frac{\pi }{6}$