赣州推广团队seo课程培训学校
目录
1. 前言
1.1 什么是基数排序⭐⭐⭐
1.2 执行流程⭐⭐⭐⭐⭐
2. 代码实现⭐⭐⭐
3. 性能分析⭐⭐
3.1 时间复杂度
3.2 空间复杂度
1. 前言
一个算法,只有理解算法的思路才是真正地认识该算法,不能单纯记住某个算法的实现代码!
1.1 什么是基数排序⭐⭐⭐
(1)通过键值得各个位的值,将要排序的元素分配至一些桶中,达到排序的作用
(2)基数排序法是属于稳定性的排序,基数排序法是效率高的稳定排序法
(3)基数排序是桶排序的扩展
注意:我们这里谈论的数组都是Int类型,代码实现的基数排序也是针对正整数的排序!
详细说明:
基数排序的思想是“多关键字排序”。基数排序有两种实现方式:第一种叫作最高位优先,即先按最高位排成若干子序列,再对每个子序列按次高位排序。举扑克牌的例子,就是先按花色排成4个子序列,再对每种花色的13张牌进行排序,最终使所有扑克牌整体有序。第二种叫作最低位优先,这种方式不必分成子序列,每次排序全体关键字都参与。最低位可以优先这样进行,不通过比较,而是通过“分配”和“收集”。还是扑克牌的例子,可以先按数字将牌分配到13个桶中,然后从第一个桶开始依次收集:再将收集好的牌按花色分配到4个桶中,然后还是从第一个桶开始依次收集。经过两次“分配”和“收集”操作,最终使牌有序。
我们这里介绍的是按最低位优先!
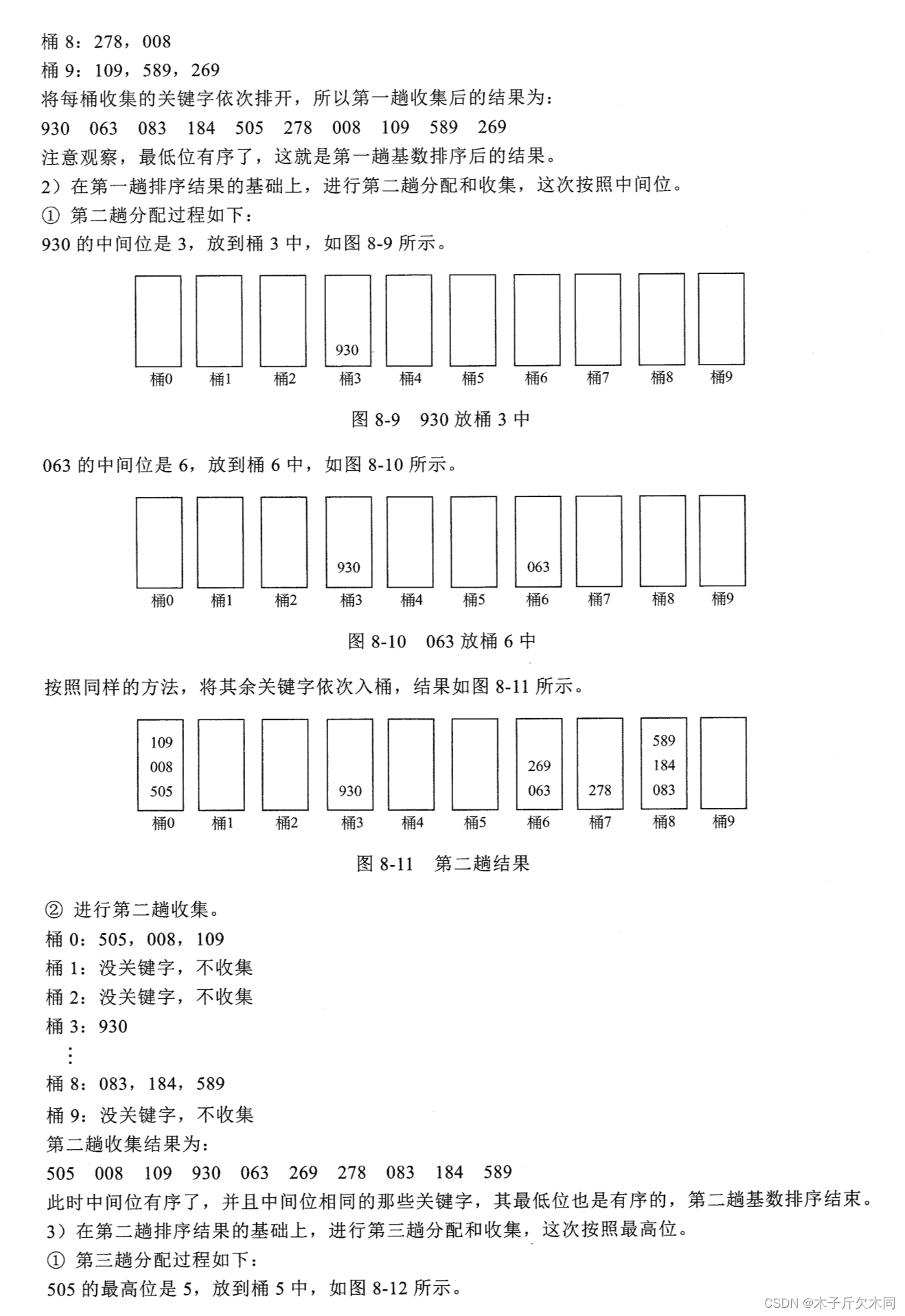
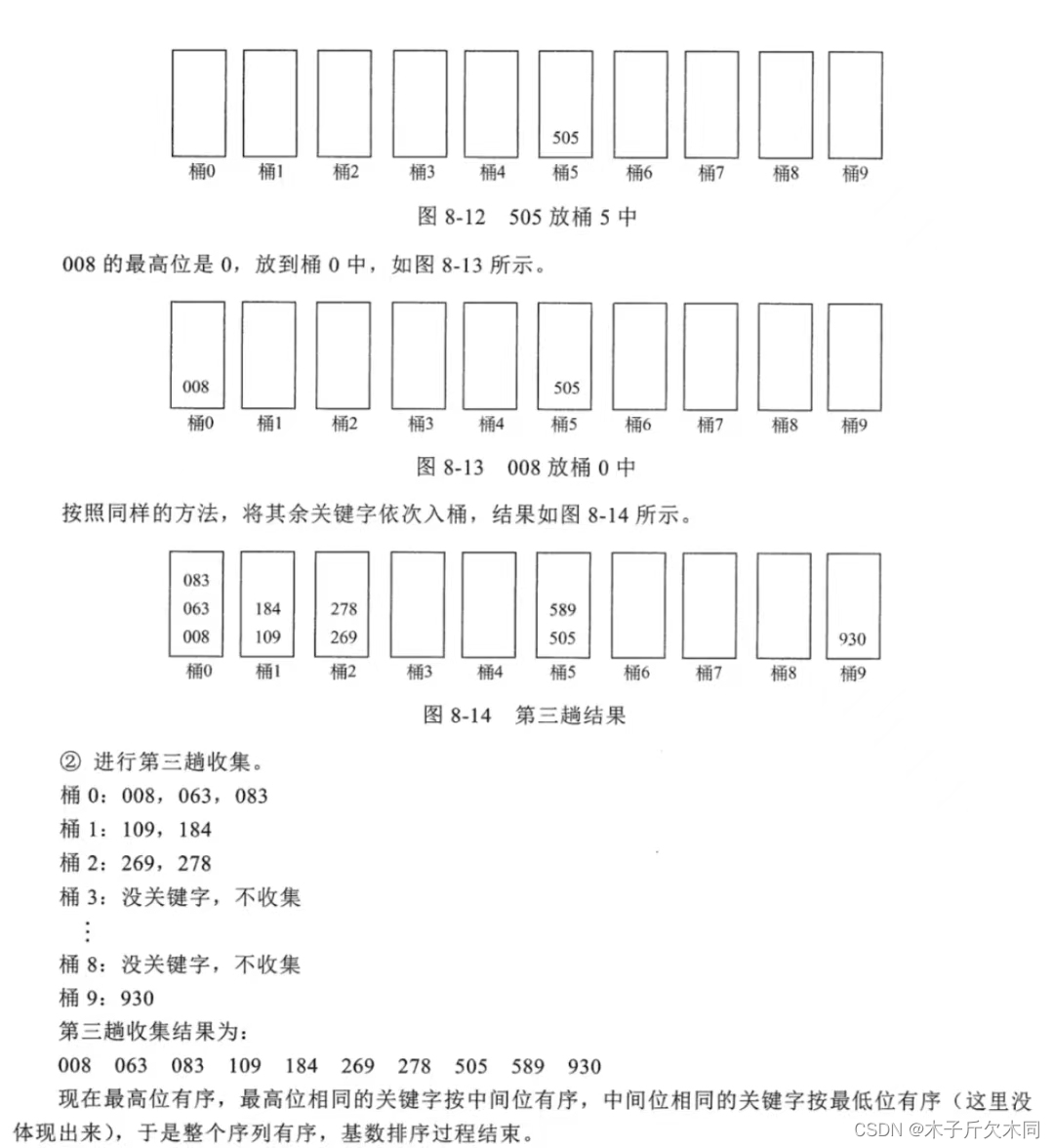
1.2 执行流程⭐⭐⭐⭐⭐
- 图示说明

- 文字说明
初始桶如图8 - 5 所示:

2. 代码实现⭐⭐⭐
代码的实现分为三大步:
第一步:先找到这组数组的最大值max,因为最大值关乎到后续找“位”的次数。如果最大值是123,那么只需要找3“位”,也就是需要分装3次。如果最大值是1234,那么需要找4“位”,也就是需要分装4次。
第二步:创建一个队列数组,其元素的类型是队列(用LinkedList来表示),一个桶就是一个队列,队列满足桶的要求,所以选用队列来充当桶。如果传进来的数组元素类型是int型,我们可以确定只需要10个桶,10个桶分别代表0、1、2、3、4、5、6、7、8、9。
第三步:分装和收集。这里面又分为两小步,分装、收集。具体实现看代码。
public static void radixSort(int[] array){//1. 先确定最大值,方便后期遍历int max = 0;for(int x : array) {max = Math.max(max,x);}//2. 创建队列,因为我们这里是四10个数字,所以创建10个队列,使用LinkedList来代替队列//此时创建的queueList里面的元素类型都是Queue<Integer>,也就是指针,他们执行的区域还没有开辟,需要使用new 挨个去开辟Queue<Integer>[] queueList = new LinkedList[10];//为里面的元素赋值,给一个队列for(int i = 0;i < queueList.length;i++){queueList[i] = new LinkedList<>();}//3. 开始分类和收集/*123 / 1(divider) % 10 = 3123 / 10(divider) % 10 = 2123 / 100(divider) % 10 = 1*///最大值的作用体现了,限制了divider的移动//divider不断地往1,10,100直至大于max扩大for(int divider = 1;divider <= max;divider *= 10){//3.1 分桶(也是分类)for(int x : array){int index = x / divider % 10;queueList[index].offer(x);}//3.2 收集(还原原来数组)int i = 0;//定义原来数组的下标for(Queue<Integer> queue1 : queueList){while(queue1.peek() != null){array[i] = queue1.poll();i++;}}}}public static void main(String[] args) {int[] a = {10,9,8,7,6,5,4,3,2,1};Sort.radixSort(a);for (int x : a) {System.out.print(x + " ");}}
3. 性能分析⭐⭐
3.1 时间复杂度
假设有一个长度为N,数组元素的类型都是int型的数组需要排序,其中最大元素是x,它的位数是k位,那么时间复杂度就是:
① 需要分装的次数 = 位数k乘以总的数组长度N(因为每分装一次,就相当于遍历一下数组) = O(k*N)
② 需要收集的次数(极端情况:在第一次分装的时候都在一个桶内,遍历桶的个数也就是N) = 每个桶的peek次数 + 桶的总长度10 = O(10 + N)
总的时间复杂度为:
3.2 空间复杂度
基数排序需要10个桶,每个桶又是一个队列,10个桶又需要分桶装N个数组元素。
则空间复杂度为:
