seo网站建设及扩词搜索引擎seo是什么意思

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

如果一个节点能够在它的左右子树中分别找到p和q，则该节点为LCA节点

class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {return find(root, p.val, q.val);}// 在二叉树中寻找 val1 和 val2 的最近公共祖先节点   private TreeNode find(TreeNode root, int val1, int val2){if(root == null) return null;// 前序位置if(root.val == val1 || root.val == val2){// 如果遇到目标值，直接返回return root;}TreeNode left = find(root.left, val1, val2);TreeNode right = find(root.right, val1, val2);// 后序位置，已经知道左右子树是否存在目标值if(left != null && right != null){return root;}return left != null ? left : right;}
}

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Mwos0c4s-1681899253749)(E:/typora/binarysearchtree_improved.png)]

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

但对于 BST 来说，根本不需要老老实实去遍历子树，由于 BST 左小右大的性质，将当前节点的值与val1和val2作对比即可判断当前节点是不是LCA：

假设val1 < val2，那么val1 <= root.val <= val2则说明当前节点就是LCA；若root.val比val1还小，则需要去值更大的右子树寻找LCA；若root.val比val2还大，则需要去值更小的左子树寻找LCA。

class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {// 保证 val1 较小，val2 较大int val1 = Math.min(p.val, q.val);int val2 = Math.max(p.val, q.val);return find(root, val1, val2);}// 在 BST 中寻找 val1 和 val2 的最近公共祖先节点private TreeNode find(TreeNode root, int val1, int val2){if(root == null) return null;if(root.val > val2){// 当前节点太大，去左子树找return find(root.left, val1, val2);}if(root.val < val1){// 当前节点太小，去右子树找return find(root.right, val1, val2);}// val1 <= root.val <= val2// 则当前节点就是最近公共祖先return root;}
}

这道题目跟👆一样

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5OrUzHc7-1681899253750)(E:/typora/binarysearchtree_improved.png)]

class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {// 保证 val1 较小，val2 较大int val1 = Math.min(p.val, q.val);int val2 = Math.max(p.val, q.val);return find(root, val1, val2);}// 在 BST 中寻找 val1 和 val2 的最近公共祖先节点private TreeNode find(TreeNode root, int val1, int val2){if(root == null) return null;if(root.val > val2){// 当前节点太大，去左子树找return find(root.left, val1, val2);}if(root.val < val1){// 当前节点太小，去右子树找return find(root.right, val1, val2);}// val1 <= root.val <= val2// 则当前节点就是最近公共祖先return root;}
}

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

完全二叉树如下图，每一层都是紧凑靠左排列的：

满二叉树如下图，是一种特殊的完全二叉树，每层都是是满的，像一个稳定的三角形

一棵完全二叉树的两棵子树，至少有一棵是满二叉树：

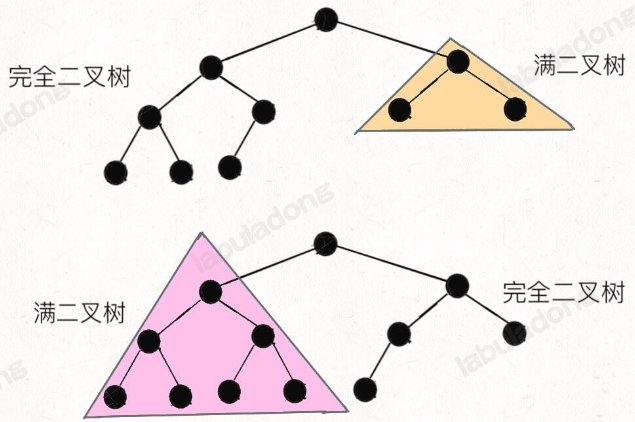
如何求一棵完全二叉树的节点个数呢？

如果是一个普通二叉树，显然只要向下面这样遍历一边即可，时间复杂度 O(N)

public int countNodes(TreeNode root) {if (root == null) return 0;return 1 + countNodes(root.left) + countNodes(root.right);
}

那如果是一棵满二叉树，节点总数就和树的高度呈指数关系

public int countNodes(TreeNode root) {int h = 0;// 计算树的高度while (root != null) {root = root.left;h++;}// 节点总数就是 2^h - 1return (int)Math.pow(2, h) - 1;
}

完全二叉树比普通二叉树特殊，但又没有满二叉树那么特殊，计算它的节点总数，可以说是普通二叉树和完全二叉树的结合版

public int countNodes(TreeNode root) {TreeNode l = root, r = root;// 沿最左侧和最右侧分别计算高度int hl = 0, hr = 0;while (l != null) {l = l.left;hl++;}while (r != null) {r = r.right;hr++;}// 如果左右侧计算的高度相同，则是一棵满二叉树if (hl == hr) {return (int)Math.pow(2, hl) - 1;}// 如果左右侧的高度不同，则按照普通二叉树的逻辑计算return 1 + countNodes(root.left) + countNodes(root.right);
}

算法的递归深度就是树的高度 O(logN)，每次递归所花费的时间就是 while 循环，需要 O(logN)，所以总体的时间复杂度是 O(logN*logN)

–end–