做地方的门户网站网络销售平台有哪些
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:子树中标签相同的结点数
出处:1519. 子树中标签相同的结点数
难度
5 级
题目描述
要求
给你一个树(即一个连通的无向无环图),这个树由编号从 0 \texttt{0} 0 到 n − 1 \texttt{n} - \texttt{1} n−1 的 n \texttt{n} n 个结点和 n − 1 \texttt{n} - \texttt{1} n−1 条边 edges \texttt{edges} edges 组成。树的根结点为结点 0 \texttt{0} 0,树中的每一个结点都有一个标签,标签是字符串 labels \texttt{labels} labels 中的一个小写字符(编号为 i \texttt{i} i 的结点的标签是 labels[i] \texttt{labels[i]} labels[i])。
边数组 edges \texttt{edges} edges 以 edges[i] = [a i , b i ] \texttt{edges[i] = [a}_\texttt{i}\texttt{, b}_\texttt{i}\texttt{]} edges[i] = [ai, bi] 的形式给出,该格式表示结点 a i \texttt{a}_\texttt{i} ai 和 b i \texttt{b}_\texttt{i} bi 之间存在一条边。
返回一个大小为 n \texttt{n} n 的数组 ans \texttt{ans} ans,其中 ans[i] \texttt{ans[i]} ans[i] 表示第 i \texttt{i} i 个结点的子树中与结点 i \texttt{i} i 标签相同的结点数。
树 T \texttt{T} T 的子树是由 T \texttt{T} T 中的某个结点及其所有后代结点组成的树。
示例
示例 1:

输入: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd" \texttt{n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"} n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
输出: [2,1,1,1,1,1,1] \texttt{[2,1,1,1,1,1,1]} [2,1,1,1,1,1,1]
解释:结点 0 \texttt{0} 0 的标签为 ‘a’ \texttt{`a'} ‘a’ ,以 ‘a’ \texttt{`a'} ‘a’ 为根结点的子树中,结点 2 \texttt{2} 2 的标签也是 ‘a’ \texttt{`a'} ‘a’,因此答案为 2 \texttt{2} 2。注意树中的每个结点都是这个子树的一部分。
结点 1 \texttt{1} 1 的标签为 ‘b’ \texttt{`b'} ‘b’,结点 1 \texttt{1} 1 的子树包含结点 1 \texttt{1} 1、 4 \texttt{4} 4 和 5 \texttt{5} 5,由于结点 4 \texttt{4} 4、 5 \texttt{5} 5 的标签与结点 1 \texttt{1} 1 不同,因此答案为 1 \texttt{1} 1(该结点本身)。
示例 2:
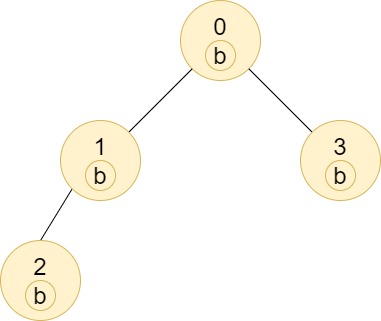
输入: n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb" \texttt{n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"} n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
输出: [4,2,1,1] \texttt{[4,2,1,1]} [4,2,1,1]
解释:结点 2 \texttt{2} 2 的子树中只有结点 2 \texttt{2} 2,因此答案为 1 \texttt{1} 1。
结点 3 \texttt{3} 3 的子树中只有结点 3 \texttt{3} 3,因此答案为 1 \texttt{1} 1。
结点 1 \texttt{1} 1 的子树中包含结点 1 \texttt{1} 1 和 2 \texttt{2} 2,标签都是 ‘b’ \texttt{`b'} ‘b’,因此答案为 2 \texttt{2} 2。
结点 0 \texttt{0} 0 的子树中包含结点 0 \texttt{0} 0、 1 \texttt{1} 1、 2 \texttt{2} 2 和 3 \texttt{3} 3,标签都是 ‘b’ \texttt{`b'} ‘b’,因此答案为 4 \texttt{4} 4。
示例 3:
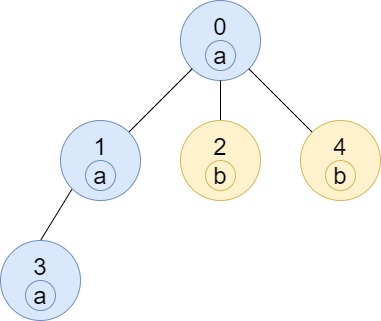
输入: n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab" \texttt{n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"} n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
输出: [3,2,1,1,1] \texttt{[3,2,1,1,1]} [3,2,1,1,1]
数据范围
- 1 ≤ n ≤ 10 5 \texttt{1} \le \texttt{n} \le \texttt{10}^\texttt{5} 1≤n≤105
- edges.length = n − 1 \texttt{edges.length} = \texttt{n} - \texttt{1} edges.length=n−1
- edges[i].length = 2 \texttt{edges[i].length} = \texttt{2} edges[i].length=2
- 0 ≤ a i , b i < n \texttt{0} \le \texttt{a}_\texttt{i}\texttt{, b}_\texttt{i} < \texttt{n} 0≤ai, bi<n
- a i ≠ b i \texttt{a}_\texttt{i} \ne \texttt{b}_\texttt{i} ai=bi
- labels.length = n \texttt{labels.length} = \texttt{n} labels.length=n
- labels \texttt{labels} labels 仅由小写英语字母组成
解法
思路和算法
这道题中的树是一个无向无环的连通图,规定根结点是结点 0 0 0,其余结点之间只能知道连通关系。为了得到相邻结点之间的父结点和子结点的关系,需要根据给定的边得到每个结点的相邻结点,然后从根结点开始遍历树。在确定所有相邻结点之间的父结点和子结点的关系之后,即可得到每个子树中包含的结点。对于每个子树,遍历子树中的每个结点即可得到与子树根结点标签相同的结点数。
由于树中的结点数 n n n 最大可达 1 0 5 10^5 105,因此应该尽量避免重复访问结点,而是每个结点都访问一次。由于树中的每个标签的出现次数由树的根结点标签与每个子树中的每个标签的出现次数决定,因此可以使用后序遍历的方式得到每个子树中的每个标签的出现次数,然后得到每个子树中与子树根结点标签相同的结点数。
对于每个子树,需要使用哈希表记录子树中每个标签的出现次数。当子树中只有一个结点时,只有子树根结点的标签出现 1 1 1 次,其余标签都不出现;当子树的根结点有子结点时,将每个子结点对应的每个标签的出现次数加到子树根结点的每个标签的出现次数,最后将子树根结点的标签的出现次数加 1 1 1,即可得到子树中每个标签的出现次数。
实现方面有以下两点说明。
-
由于标签只包含小写英语字母,因此可以使用长度为 26 26 26 的数组代替哈希表记录每个标签的出现次数。
-
遍历过程中需要知道相邻结点之间的父结点和子结点的关系。由于和一个结点相邻的结点只有该结点的父结点和全部子结点,一种方法是在遍历过程中传入当前结点的父结点编号,在遍历与当前结点相邻的结点时跳过父结点,则可确保只会访问当前结点的子结点。
代码
class Solution {String labels;List<Integer>[] adjacentNodes;int[][] counts;public int[] countSubTrees(int n, int[][] edges, String labels) {this.labels = labels;adjacentNodes = new List[n];for (int i = 0; i < n; i++) {adjacentNodes[i] = new ArrayList<Integer>();}for (int[] edge : edges) {int node0 = edge[0], node1 = edge[1];adjacentNodes[node0].add(node1);adjacentNodes[node1].add(node0);}counts = new int[n][26];postorder(0, -1);int[] ans = new int[n];for (int i = 0; i < n; i++) {char c = labels.charAt(i);ans[i] = counts[i][c - 'a'];}return ans;}public void postorder(int node, int parent) {char c = labels.charAt(node);List<Integer> adjacent = adjacentNodes[node];for (int next : adjacent) {if (next == parent) {continue;}postorder(next, node);for (int i = 0; i < 26; i++) {counts[node][i] += counts[next][i];}}counts[node][c - 'a']++;}
}
复杂度分析
-
时间复杂度: O ( n × ∣ Σ ∣ ) O(n \times |\Sigma|) O(n×∣Σ∣),其中 n n n 是树的结点数, Σ \Sigma Σ 是字符集,这道题中 Σ \Sigma Σ 是全部小写英语字母, ∣ Σ ∣ = 26 |\Sigma| = 26 ∣Σ∣=26。后序遍历需要访问每个结点一次,对于每个结点需要 O ( ∣ Σ ∣ ) O(|\Sigma|) O(∣Σ∣) 的时间计算以该结点为根结点的子树中的每个标签的出现次数。
-
空间复杂度: O ( n × ∣ Σ ∣ ) O(n \times |\Sigma|) O(n×∣Σ∣),其中 n n n 是树的结点数, Σ \Sigma Σ 是字符集,这道题中 Σ \Sigma Σ 是全部小写英语字母, ∣ Σ ∣ = 26 |\Sigma| = 26 ∣Σ∣=26。空间复杂度包括存储相邻结点信息的空间、哈希表空间和递归调用的栈空间,存储相邻结点信息的空间是 O ( n ) O(n) O(n),哈希表空间是 O ( n × ∣ Σ ∣ ) O(n \times |\Sigma|) O(n×∣Σ∣),即每个结点需要 O ( ∣ Σ ∣ ) O(|\Sigma|) O(∣Σ∣) 的空间记录以该结点为根结点的子树中的每个标签的出现次数,递归调用的栈空间在最坏情况下是 O ( n ) O(n) O(n),因此空间复杂度是 O ( n × ∣ Σ ∣ ) O(n \times |\Sigma|) O(n×∣Σ∣)。
