b2b2c网站百度下载app下载安装到手机

一、说明

        欢迎回到这个三部曲的第二部分！在第一部分中，我们为测度论概率奠定了基础。我们探索了测量和可测量空间的概念，并使用这些概念定义了概率空间。在本文中，我们使用测度论来理解随机变量。

        作为一个小回顾，在第一部分中，我们看到概率空间可以使用测度理论按以下方式定义：

        现在，我们将考虑范围扩展到随机变量。在学校中，通常引入随机变量作为其值是随机的变量。例如，掷骰子的结果可以通过随机变量X建模，其值随机为 1、2、3、4、5 或 6。虽然这个定义适用于概率的基本应用，但它是一点也不严谨，并且错过了一些非常令人满意的直觉。

二、可测量的功能

        因此，我们现在转向测度理论来定义随机变量。为了做到这一点，我们必须定义一个可测量的函数：

        让我们分解一下这个定义。首先，与任何其他函数一样，可测量函数将一个集合中的元素映射到另一个集合。但这还不是全部，这个函数还有更多维度。函数f的域和余域都是分别配备有 σ 代数 ℱ 和 ℳ 的可测空间。而且，最重要的是，可测量函数可以将测量从域的可测量空间“传输”到共域的可测量空间。这是什么意思？假设可测空间(F, ℱ ) 的测度为µ。然后，我们可以应用f来获得可测空间 (M, ℳ) 的测度。如何？出色地，

        而且，我们已经定义了一个可测函数，f⁻1( A)肯定属于F的 σ 代数，因此可以通过测度 µ 来指定。

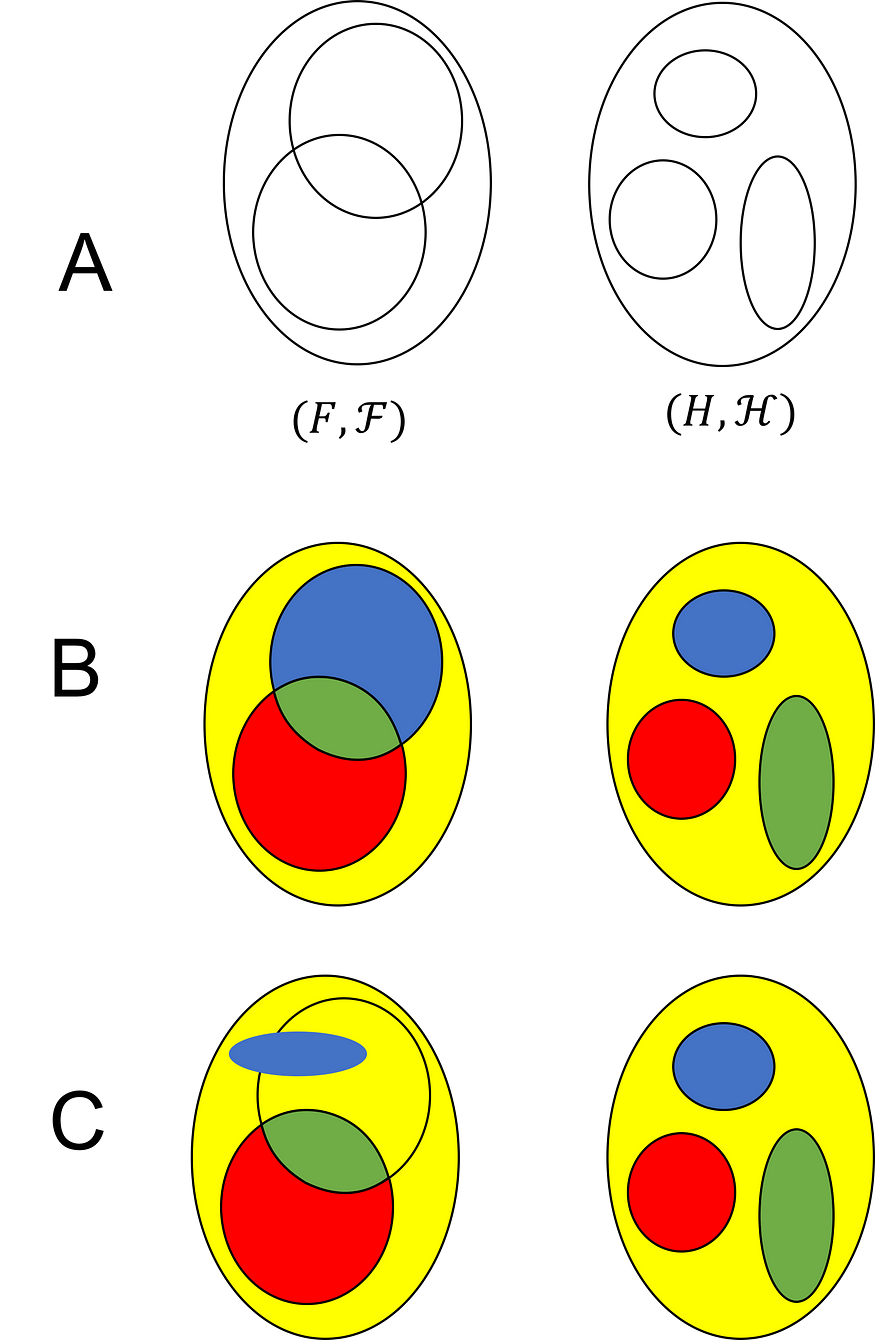
图片来源：马修·伯恩斯坦

        该图的 A 部分描绘了两个可测量空间(F,ℱ)和(H,ℋ)。σ 代数由黑线概述的集合生成。B 部分描述了将F映射到H的有效可测量函数f。即，左边的集合是域，右边的集合是共域。颜色说明f下F和H的子集之间的图像关系。例如，F中的蓝色集合的图像是H中的蓝色集合。我们看到ℋ的每个成员都有一个可测量的原像。C 部分描述了一个不可测量的函数。该函数是不可测量的，因为ℋ中的蓝色集具有不属于 ℱ 成员的原像。

三、随机变量

        现在我们已经定义了可测量函数，我们可以开始处理随机变量。使用测度论，我们按以下方式定义随机变量：

        这说明了什么？简而言之，随机变量是将概率空间中的元素映射到可测量空间的函数。如果您还记得的话，集合 Ω 称为样本空间，代表所有可能的未来。随机变量X简单地将每个可想象的未来映射到某个集合F中的元素。集合F是X可以取的所有可能值的集合。随机变量是概率空间中的可测量函数，因为它允许我们将概率测量从概率空间“传输”到我们正在考虑的X结果集。

四、离散随机变量

        为了说明这一点，我们考虑抛硬币。令Y为随机变量，代表抛掷一枚公平硬币的结果。然后，集合 Ω 代表所有可能的未来——硬币在空中旋转、着陆、弹跳等的无限种方式。随机变量将每个未来映射到可测量的空间(H, ℋ)，其中H:={ 0,1}。在这里，我们将反面编码为 0，将正面编码为 1。例如，硬币可以有两种方式a和b，其中硬币在空中翻转并落地为正面。那么X(a)=1并且X(b)=1。

        H 上的 σ 代数表示我们希望为其分配概率的所有结果组：

        这里需要注意的是，ℋ中的每个元素在原始概率空间中的X下都有一个原像，即该原像是E的成员。因此，我们可以根据测度为ℋ中的每个集合分配一个概率根据P得到其原像：

用熟悉的表示法来说，这很简单：P(X=1)。

五、连续随机变量

        现在，我们转向连续随机变量。这有一个稍微不同的方法，因为，很明显，如果我们采用与离散随机变量相同的方法，我们将遇到数学矛盾。

        连续随机变量还将集合 Ω 中的元素映射到集合H。但在这种情况下，H是所有实数的集合。那是，

        现在的问题是，我们不能像对待离散随机变量那样拥有 σ 代数。根据可测函数的定义，我们需要在 ℝ 上构造 σ-代数ℋ ，使得ℋ中每个元素的原像都是E中的一个事件。但是，我们不能为 ℝ 中的每个元素分配非零概率因为集合的基数是无穷大，即它是不可数无限集合。任何为集合中的每个元素分配概率的尝试都会导致 σ-代数ℋ的概率为无穷大——这是一个矛盾，因为任何事件的概率都不能大于 1。

        为了避免这个问题，我们转向Borel σ-代数。这本身就是一个广泛深入的话题，需要大量的拓扑知识，因此我们不会在本文中深入探讨。但直观上，Borel σ 代数处理的是实线上的所有区间，而不是实线本身。也就是说，实线上的区间(x,y)是 ℋ 的一个元素，因此在X下具有可测量的原像。并且，我们分配所有长度为零的区间，即仅包含一个实数的单例集，概率为0。也就是说，分配给任何特定实数的概率为零。然而，分配给实数区间的概率可以是非零的。

        现在，我们如何计算 ℋ 中区间原像的测度？大多数情况下，这是通过使用概率密度函数来实现的——概率密度函数是概率中熟悉的概念。这是通过以下方式定义的：

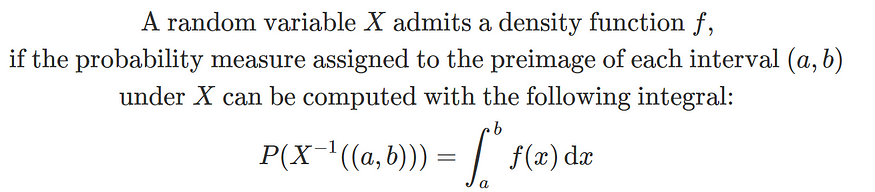
        通常，LHS 表示为P(a < X < b)。

        至此，我们现在统一了离散随机变量和连续随机变量的概念。希望这为概率论这个反直觉的怪物提供了一些令人满意的直觉。而且，我应该说，测度论不仅仅用于统一这些概念。事实上，通过以这种方式定义随机变量，我们现在已经配备了处理非数字结果（即向量、集合和函数）的随机变量所需的机制。

        本三部曲的最后一篇文章将探讨如何使用测度论来理解数学期望。

        感谢您的阅读，祝您度过愉快的一天！