网站怎么做流量互换网络营销推广难做吗

目录

二叉树

二叉搜索树的查找方式：

AVL树

AVL树节点的实现

AVL树节点的插入操作

AVL树的旋转操作

右旋转：

左旋转：

左右双旋：

右左双旋：

AVL树的不足和下期预告（红黑树）

---

二叉树

了解AVL树之前，需要先了解一下二叉搜索树的概念，二叉搜索树具有以下性质：

1，如果左子树不为空，则左子树上所有节点的值都小于跟节点的值。

2，如果右子树不为空，则右子树的所有节点的值都大于跟节点的值。

3，根节点的左右子树也是一颗二叉搜索树。

如果使用二叉树的中序遍历方法来遍历一颗二叉树，则可以得到一个有序的序列。

二叉搜索树的查找方式：

根据上图可以对二叉树进行查找从而得到我们想要的节点。

一个完全二叉树的查找效率可以达到  级别，但如果我们插入的数值都是大于根节点的数值，并且是严格递增的，那么此时整个二叉树就会退化成一个链表的结构，那么此时查找的效率也会退化成。因此我们就需要考虑一个问题，无论何时进行插入，都可以让二叉树，保持左右子树的相对平衡，随时更改根节点，这样就可以让查找的时间复杂度一直保持在,所以研究者引入了AVL树的概念。

AVL树

在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。

AVL树它本质上其实还是一个二叉树，它的特点符合二叉树的所有特点，在此之外，AVL树还具有平衡的性质，也就是说，它的左子树和右子树的高度差的绝对值不会大于1，因此这样也就保证了AVL树的查找效率。

AVL树节点的实现

为了实现AVL树，我们需要先定义树的节点，和普通的二叉树不同，在定义节点的时候，我们也需要在其中定义一个平衡因子，我们使用bf（balance factor）来表示：AVL树的节点定义如下：

class TreeNode{//定义树的左右节点索引和父亲索引public TreeNode left = null;public TreeNode right = null;public TreeNode parent = null;public int val;public int bf;//定义构造函数public TreeNode (int val){this.val = val;}
}

我们定义当前节点的平衡因子 = 右树的高度 - 左树的高度。如果当前节点的bf<0，那么左树就高，bf>0右树就高。bf = 0,那么两边一样高。当然这只是其中的一种实现方式而已（本文是这么定义的）。

AVL树节点的插入操作

首先，我们将其分为两步

1，按照二叉树的插入方式进行插入。

2，对不满足条件的节点进行旋转，使树达到平衡。

此时可以看下接下来这几幅图：

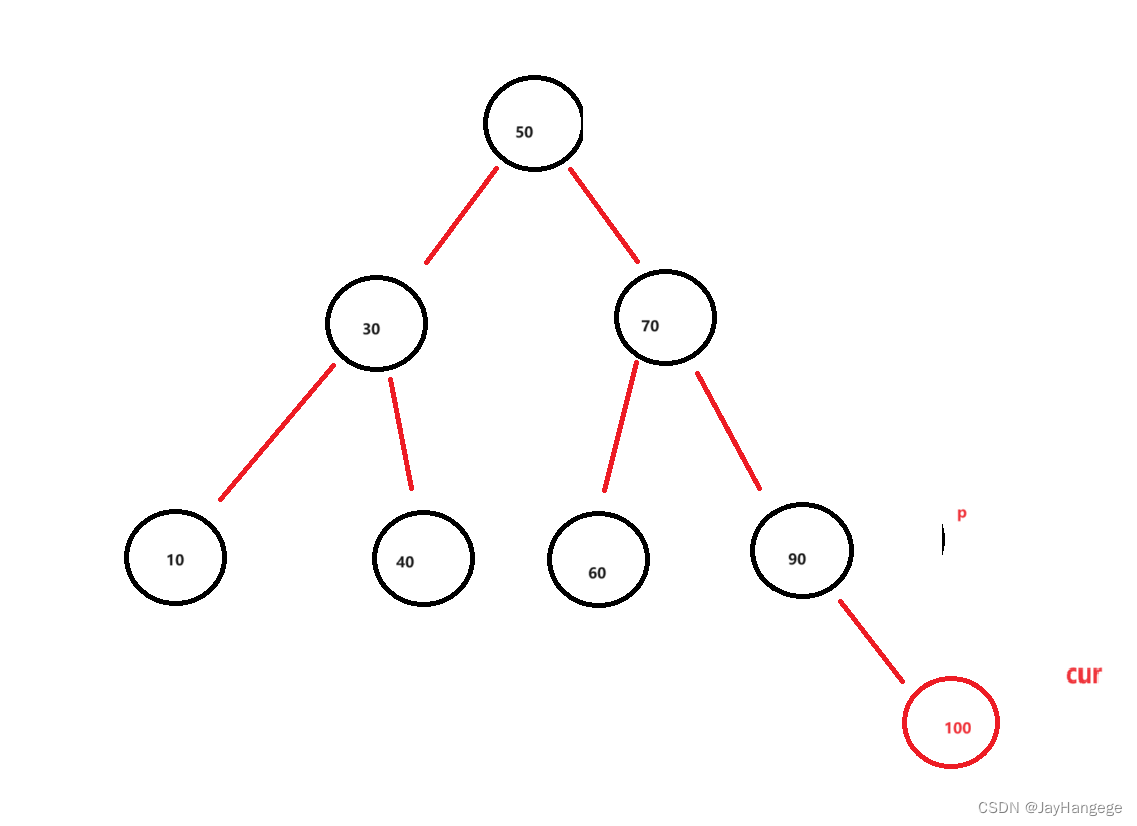假设我要在二叉树种插入一个值为100，那么此时我应该找到100应该插入到哪个位置，每一次寻找定义cur为要插入的位置，定义parent为cur的父亲节点，那么遍历下来就可以找到插入的位置，此时代码如下：

    public TreeNode root ;public void insert(int val){//1,首先先进行节点的插入操作;TreeNode node = new TreeNode(val);if(this.root == null){//如果树为空，那么node就是新的rootthis.root = node;}else{TreeNode parent = null;TreeNode cur = this.root;// 1.1 先判断要插入的位置，然后再进行插入while(cur != null){if(cur.val < val){parent = cur;cur = cur.right;} else if (cur.val == val) {return;}else{parent = cur;cur = cur.left;}}//此时找到了要插入的位置，对node进行插入，插入的位置为parent所指向的节点//判断往左边插入还是右边插入，然后再让node指回去。if(parent.val < val){parent.right = node;}else{parent.left = node;}node.parent = parent;cur = node;}}

一定要让node指向指回去，否则子节点会丢失父节点的索引。

AVL树的旋转操作

基于以上的插入，我们可以发现一个问题，就是说，如果每次都插入比上一次大的值，那么势必会让这个树退化成一个链表，那么此时树的存储结构优势将会丢掉，所以AVL树引入了旋转操作来对树进行操作。从而使得这棵树不会退化成链表。

cur插入后，parent的平衡因子一定需要调整，

在插入之前，parent的平衡因子分为三种情况：-1，0, 1

插入时分以下两种情况：  

1. 如果cur插入到parent的左侧，只需给parent的平衡因子 -1 即可  

2. 如果cur插入到parent的右侧，只需给parent的平衡因子 +1 即可  

此时：parent的平衡因子可能有三种情况：0，正负1， 正负2  

1. 如果parent的平衡因子为0，说明插入之前parent的平衡因子为正负1，插入后被调整成0，此时满足AVL树的性质，插入成功

2. 如果parent的平衡因子为正负1，说明插入前parent的平衡因子为0，插入后被更新成正负1，此时以parent为根的树的高度增加，需要继续向上更新  

3. 如果parent的平衡因子为正负2，则parent的平衡因子违反平衡树的性质，需要对其进行旋转处理

此时更新操作就如下：

            while(){//更新parent的平衡因子if(cur == parent.right){parent.bf++;}else{parent.bf--;}//更新后的平衡因子为0，说明插入后的结果是平衡的，此时无需后续操作if(parent.bf == 0){return;}if(parent.bf != 1 && parent.bf != -1){//此时需要继续向上更新if(parent.bf == 2){if(cur.bf == 1){// parent.bf == 2 cur.bf == 1}else{// parent.bf == 2 cur.bf == -1}}else{if(cur.bf == 1){// parent.bf == -2 cur.bf == 1}else{// parent.bf == -2 cur.bf == -1}}}}

那么基于以上操作，我们的更新平衡因子的模板已经搭好了，但是在什么情况下需要进行旋转呢？

右旋转：

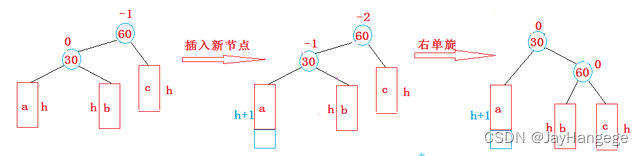
假设有上面这种情况，原来的cur.bf == 0 ， 但是parent.bf == -1 ,此时在左树的最左边插入一个节点，那么此时的节点情况就变成了cur.bf == -1 , parent.bf == -2 。那么此时就需要对parent节点进行右旋转，从而调整树的结构。

此时需要注意以下几点：

 1.  30 节点的右孩子可能存在，也可能不存在。

 2.  60 可能是根节点，也可能是子树。如果是根节点，旋转完成后，要更新根节点     如果是子树，可能是某个节点的左子树，也可能是右子树。

在上图中可以看出，当我们想进行右转操作时，需要将parent.left 标记为 subL，将subL.right标记为subLR.

从2图转换为3图可以如上图表示：

1. 修改parent.left = subLR;

2. 修改subL.right = parent;

3. 修改 subLR.parent = parent （此时需要判断subLR是否为空）

4. 保存parent的父亲节点（祖父节点）

5. 修改parent的父亲节点指向subL；

6. 修改祖父节点指向subL（需要确认祖父节点是否存在，如果不存在则parent是根节点）

7. 修改subL.parent属性为祖父节点；

8. 判断完了之后还要修改平衡因子。

代码如下：

private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;if(subLR != null){subLR.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subL;if(parent == this.root){this.root = subL;this.root.parent = null;}else{if(pParent.left == parent){pParent.left = subL;}else{pParent.right = subL;}subL.parent = pParent;}subL.bf = 0;parent.bf = 0;}

左旋转：

左旋转和右旋转的逻辑是一样的，不过是对称的操作。以下是左旋转的代码演示：

此时最初的parent的bf值为1，进行添加节点之后，则是会变成parent.bf 会变成2，此时的cur.bf

会变成1（因为给cur的右树增加了一层）。此时就需要用到左旋转的方法来进行旋转，从而降低AVL树的高度了。具体代码如下：和右旋转是对称的

 private void rotateLeft(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;parent.right = subRL;subR.left = parent;if(subRL != null){subRL.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subR;if(parent == this.root){this.root = subR;this.root.parent = null;}else{if(pParent.left == parent){pParent.left = subR;}else{pParent.right =subR;}subR.parent = pParent;}subR.bf = parent.bf = 0;}

左右双旋：

 讲完了上述两种比较简单的情况，其实还有两种比较复杂的情况，比如说，

假如说是上面这种情况呢，此时我要插入的值为40，但是60节点bf更新为-2，此时的30这个节点的bf值为1，50节点bf值为-1，这时候单纯的旋转已经无法解决这些问题了。因此

此时先对30进行左旋转：可以得到50节点bf为-2，60节点 bf 为-2，30节点 bf 为 0

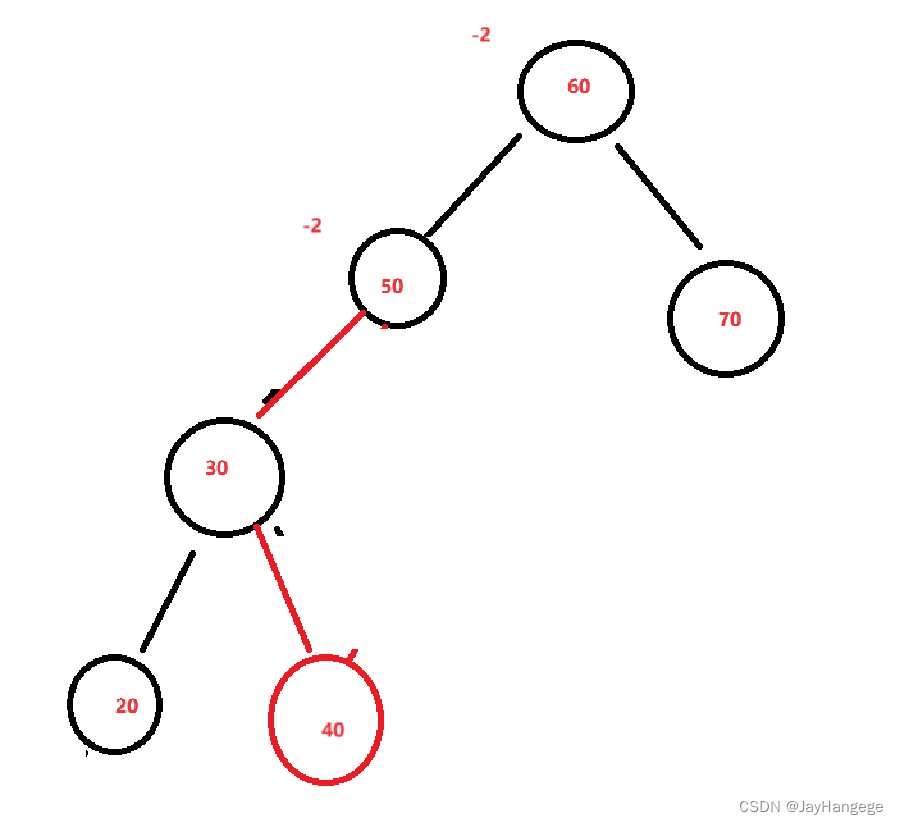
此时再对60节点进行右旋转：此时的50节点 bf 为 0 ，60节点bf为 1 此时的 AVL树已经达到了平衡。

private void rotateLR(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;int bf = subLR.bf;this.rotateRight(parent.left);this.rotateLeft(parent);if (bf == -1) {parent.bf = 1;subL.bf = 0;subLR.bf = 0;} else if (bf == 1) {subL.bf = -1;subLR.bf = 0;parent.bf = 0;}
}

右左双旋：

和左右双旋是对称的概念，此处便不再赘述了。

直接贴代码：

 private void rotateRL(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;int bf = subRL.bf;this.rotateRight(parent.right);this.rotateLeft(parent);if(bf == 1){parent.bf = -1;subR.bf = 0;subRL.bf = 0;} else if (bf == -1) {parent.bf = 0;subR.bf = 1;subRL.bf =0;}}

总之AVL树，就是为了让整个树不退化成链表，才引入的旋转机制。

AVL树的不足和下期预告（红黑树）

但是AVL树虽然保证了查询的效率，但是还是有一些机制上的问题，比如说，旋转非常消耗时间，比如我们在单旋的时候已经进行了8步操作，这只是其中的一次插入，当数据大量插入的时候AVL树显然是不够用的，因此科学家们又引入了红黑树的机制。下一次我会继续写关于红黑树的博客，希望大家能够多多点赞。