合肥网站建设-中国互联天津网站策划
目录
题目描述
解题思路
代码实现
进出栈序列理解卡特兰数分析策略
相关知识
参考文章
题目描述
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:

输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
解题思路
题目要求是计算不同二叉搜索树的个数。为此,我们可以定义两个函数:
G(n): 长度为 n 的序列能构成的不同二叉搜索树的个数。
F(i,n) 以 i为根、序列长度为 n 的不同二叉搜索树个数 (1≤i≤n)。
可见,G(n) 是我们求解需要的函数。
稍后我们将看到,G(n)可以从 F(i,n)得到,而 F(i,n)又会递归地依赖于 G(n)。
首先,根据上一节中的思路,不同的二叉搜索树的总数 G(n),是对遍历所有 i (1≤i≤n)的 F(i,n) 之和。换言之:
公式一
对于边界情况,当序列长度为 1(只有根)或为 0(空树)时,只有一种情况,即:
G(0)=1,G(1)=1
给定序列 1⋯n,我们选择数字 i 作为根,则根为 i的所有二叉搜索树的集合是左子树集合和右子树集合的笛卡尔积,对于笛卡尔积中的每个元素,加上根节点之后形成完整的二叉搜索树,如下图所示:
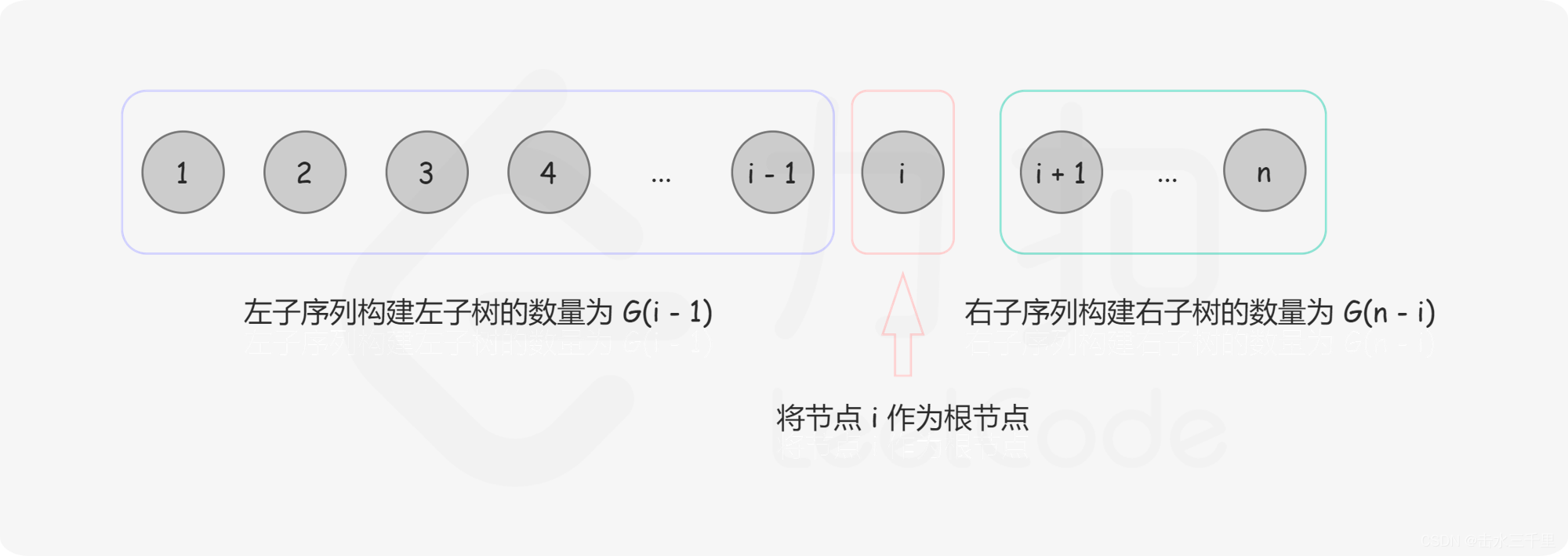
因此,我们可以得到以下公式:
公式二
F(i,n)=G(i−1)⋅G(n−i)
将公式一二 结合,可以得到 G(n的递归表达式:
事实上我们在方法一中推导出的 G(n)函数的值在数学上被称为卡塔兰数
卡塔兰数更便于计算的定义如下:
代码实现
class Solution {public int numTrees(int n) {int[] G = new int[n + 1];G[0] = 1;G[1] = 1;for (int i = 2; i <= n; ++i) {for (int j = 1; j <= i; ++j) {G[i] += G[j - 1] * G[i - j];}}return G[n];}
}进出栈序列理解卡特兰数分析策略
这是一道最经典的入门级卡特兰数题目,如果能把这题看懂,相信后面的题目也能迎刃而解。
题目
n 个元素进栈序列为:1,2,3,4,...,n,则有多少种出栈序列?
思路
我们将进栈表示为 +1,出栈表示为 -1,则 1 3 2 的出栈序列可以表示为:+1 -1 +1 +1 -1 -1。

根据栈本身的特点,每次出栈的时候,必定之前有元素入栈,即对于每个 -1 前面都有一个 +1 相对应。因此,出栈序列的所有前缀和必然大于等于 0,并且 +1 的数量等于 -1 的数量。
接下来让我们观察一下 n = 3 的一种出栈序列:+1 -1 -1 +1 -1 +1。序列前三项和小于 0,显然这是个非法的序列。
如果将第一个前缀和小于 0 的前缀,即前三项元素都进行取反,就会得到:-1 +1 +1 +1 -1 +1。此时有 3 + 1 个 +1 以及 3 - 1 个 -1。
因为这个小于 0 的前缀和必然是 -1,且 -1 比 +1 多一个,取反后,-1 比 +1 少一个,则 +1 变为 n + 1 个,且 -1 变为 n - 1 个。进一步推广,对于 n 元素的每种非法出栈序列,都会对应一个含有 n + 1 个 +1 以及 n - 1 个 -1 的序列。
如何证明这两种序列是一一对应的?
假设非法序列为 A,对应的序列为 B。每个 A 只有一个"第一个前缀和小于 0 的前缀",所以每个 A 只能产生一个 B。而每个 B 想要还原到 A,就需要找到"第一个前缀和大于 0 的前缀",显然 B 也只能产生一个 A。
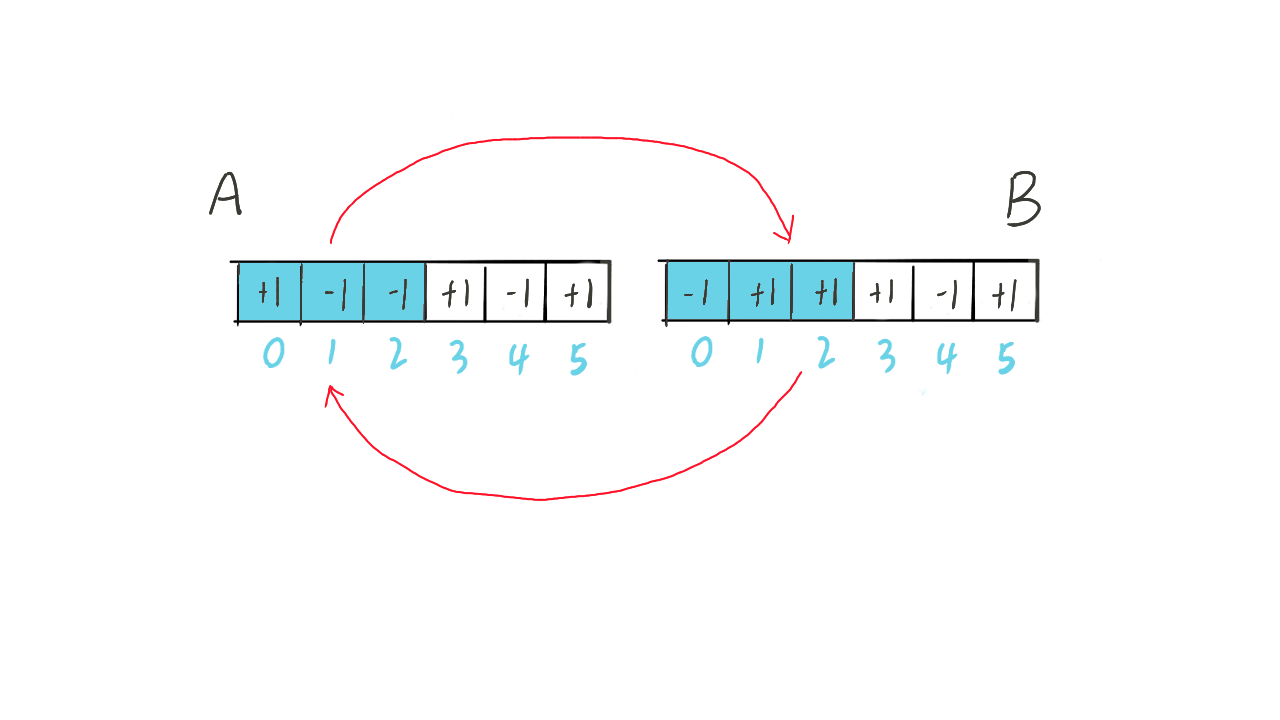
每个 B 都有 n + 1 个 +1 以及 n - 1 个 -1,因此 B 的数量为 相当于在长度为 2n 的序列中找到
n + 1 个位置存放 +1。相应的,非法序列的数量也就等于。
出栈序列的总数量共有,因此,合法的出栈序列的数量为
此时我们就得到了卡特兰数的通项
相关知识
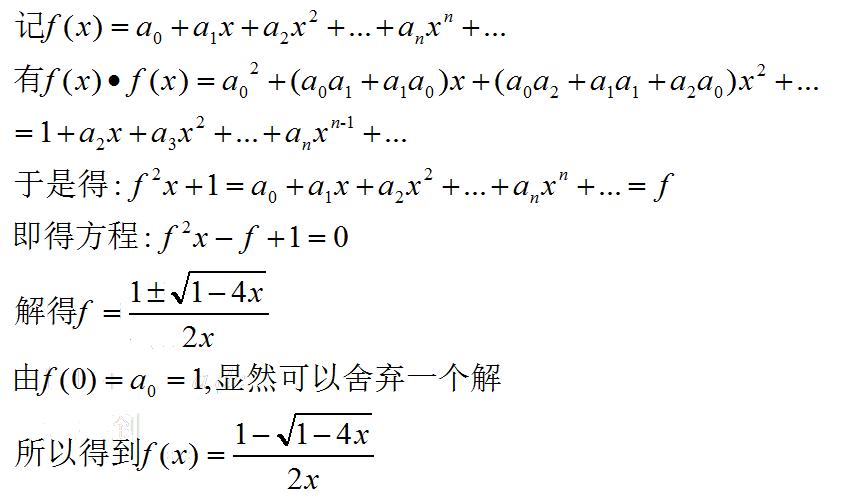
顺便提一下,这里f(0)=1,
但是看表达式的话x=0是没定义的,
所以这里是极限意义上的,
然后补充该点定义即可,
再详细的细节就不深究了...
可以验证极限是否是1:
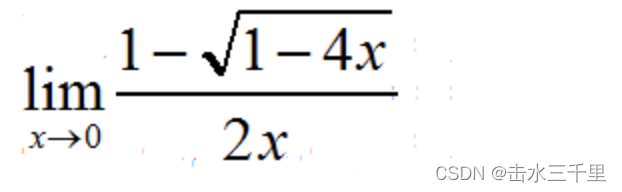
令1-4x=t 那么
当 时 的泰勒展开公式:
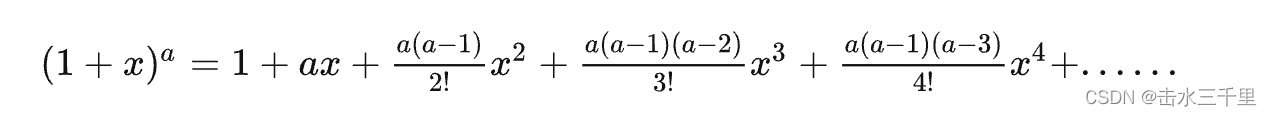

这个通项看起来太不和谐了,
还是再整理一下吧:
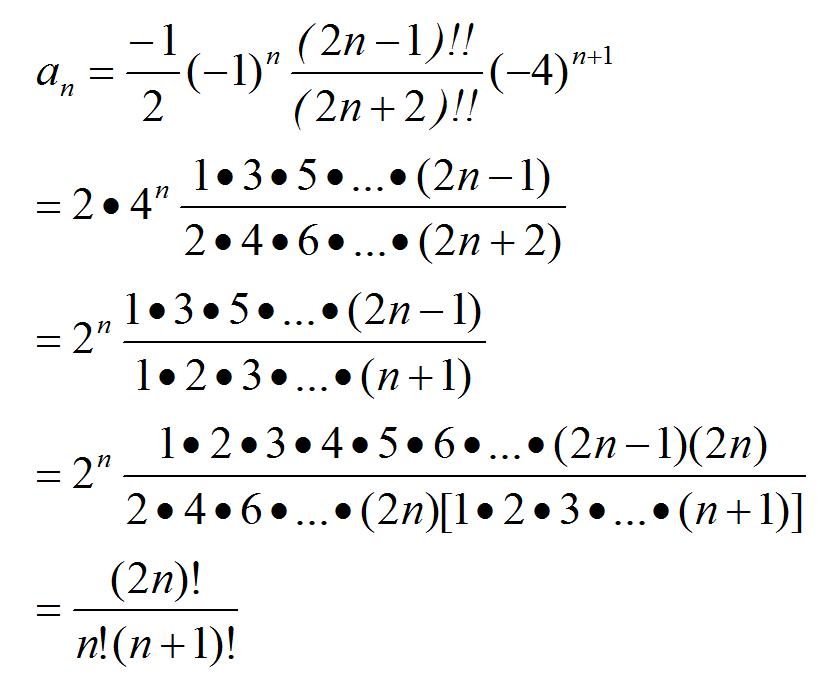
参考文章
由递推式求catalan数列通项公式
「算法入门笔记」卡特兰数
不同的二叉搜索树

