网站建设色彩设计有什么用网站排名优化培训课程

一、在排序数组中查找数字

题目传送门
法一：暴力解
直接遍历然后计数

法二：二分法求边界
看到关键字排序数组、有序数组，一定要想到二分的方法，效率高，思路也比较简单

思路：使用二分法、找数组的左边界(left)和右边界(right)，最后目标数字个数就是right-left+1
对于二分法，我们可以分别求左边界和右边界，也可以二分求左边界之后接着遍历计数，两种情况对应在真实场景下连续相等的数据一般有多长。如果经常出现很长一串连续相等的数据，就用二分法求右边界，否则容易使算法退化到O(N)。PS: 在C ++11 标准中，nums.size()的时间复杂度是Constant常数级，O(1)

class Solution {
public:int search(vector<int>& nums, int target) {int res=0;int idx=getFirstIndex(nums,target);if(idx==-1) return res;for(int i=idx;i<nums.size()&&nums[i]==target;i++){res++;}return res;}int getFirstIndex(vector<int> & nums,int target){int left=0;int right=nums.size()-1;int res=-1;while(left<=right){int mid=(left+right)/2;if(nums[mid]>target){right=mid-1;}else if(nums[mid]<target){left=mid+1;}else{res=mid;right=mid-1;}  }return res;}
};

标准解法：

class Solution {
public:int binarySearch(vector<int>& nums, int target, bool lower) {int left = 0, right = (int)nums.size() - 1, ans = (int)nums.size();while (left <= right) {int mid = (left + right) / 2;if (nums[mid] > target || (lower && nums[mid] >= target)) {right = mid - 1;ans = mid;} else {left = mid + 1;}}return ans;}int search(vector<int>& nums, int target) {int leftIdx = binarySearch(nums, target, true);int rightIdx = binarySearch(nums, target, false) - 1;if (leftIdx <= rightIdx && rightIdx < nums.size() && nums[leftIdx] == target && nums[rightIdx] == target) {return rightIdx - leftIdx + 1;}return 0;}
};

二、0~n-1中缺失的数字

题目传送门

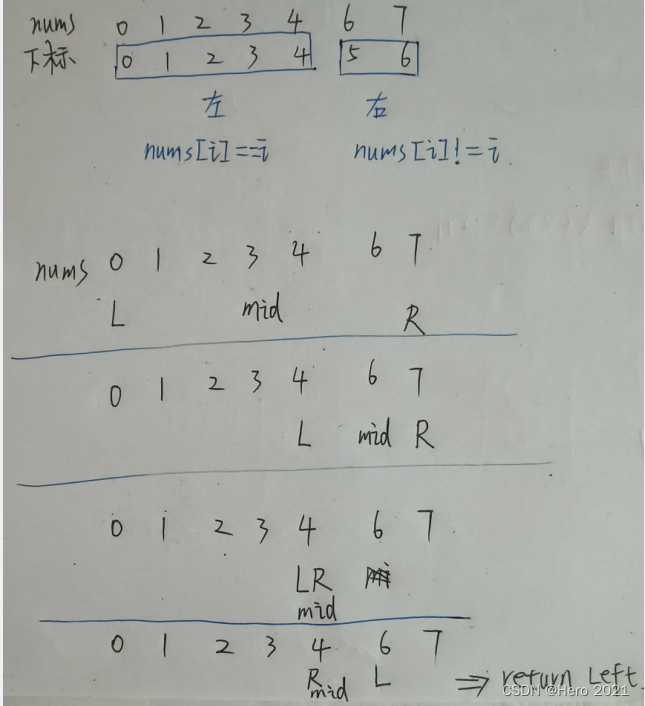
思路：因为有序，所以可以看看下标是否等于数组中的对应元素
初始化： 左边界 left = 0 ，右边界 right = len(nums)−1 ；代表闭区间 [left, right] 。
循环二分： 当 left ≤ right 时循环 （即当闭区间 [left, right] 为空时跳出） ；
1、计算中点 mid = (left + right)//2 ，其中 “//” 为向下取整除法；
2、若 nums[mid] = mid ，说明mid前面的元素肯定都是完整的不少元素所以只需要继续二分右边的数组即可，则 “右子数组的首位元素” 一定在闭区间 [mid+1, right] 中，因此执行 left = mid+1；
3、若 nums[mid] != mid ，说明mid前面的元素就有少的所以只要继续二分左边的数组即可，则 “左子数组的末位元素” 一定在闭区间 [left, mid−1] 中，因此执行 right = mid−1；
4返回值： 跳出时，变量 i 和 j 分别指向 “右子数组的首元素” 和 “左子数组的末元素” 。因此返回 i 即可。

class Solution {
public:int missingNumber(vector<int>& nums) {int left=0,right=nums.size()-1;while(left<=right){int mid=(left+right)/2;if(nums[mid]==mid){left=mid+1;}else{right=mid-1;}}return left;}
};

三、旋转数组的最小数字

题目传送门
题目分析
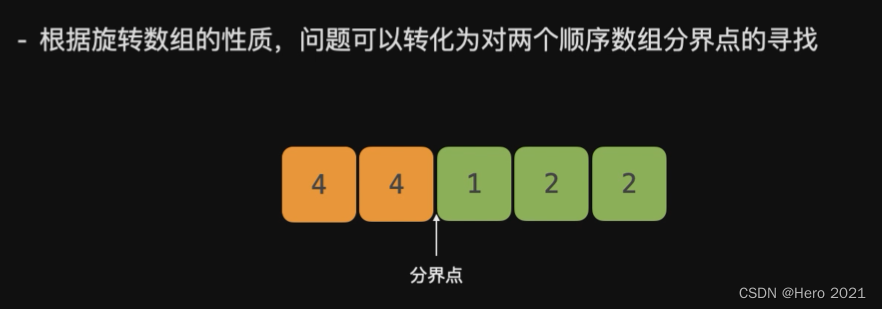
旋转数组：把一个有重复数字的有序数组，末位一部分移动到头部，这就叫做旋转数组。在这里插入图片描述

我们的目标就是找到这个分界点！

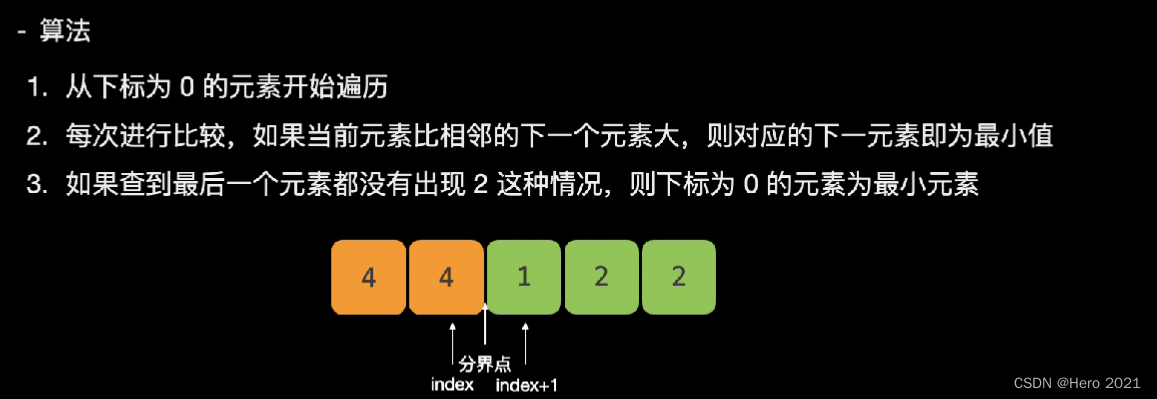
法一：暴力
分界点右边的第一个数字就是我们要找的最小数字

其实可以类比数学中的找极点

class Solution {
public:int minArray(vector<int>& numbers) {// 注意i=0开始，要越界，特殊处理一下，从1开始可以避免for(int i=1;i<numbers.size();i++){if(numbers[i-1]>numbers[i])return numbers[i];}return numbers[0];}
};

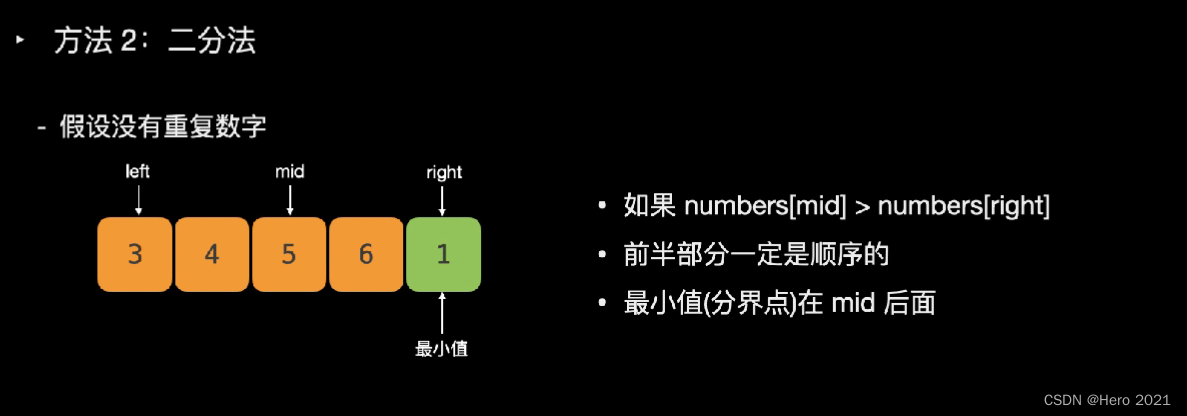
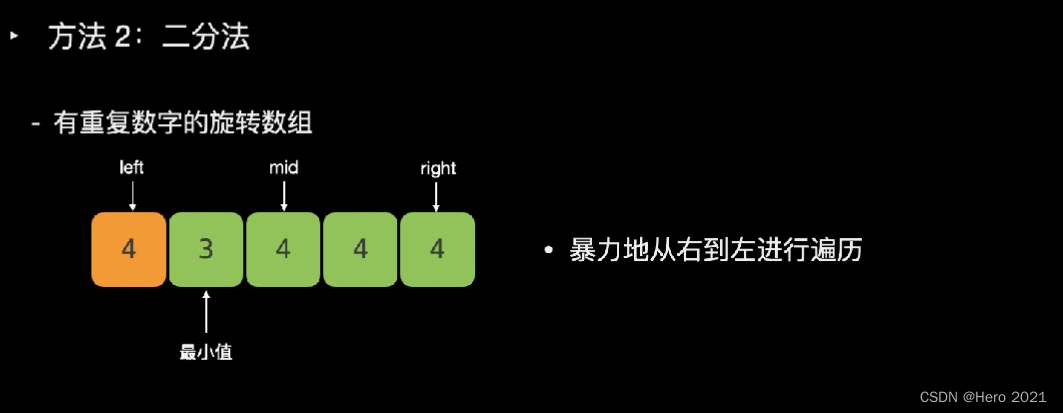
法二：二分法
题目说了，可能存在重复的数字


---------------------===

class Solution {
public:int minArray(vector<int>& numbers) {int left=0;int right=numbers.size()-1;if(right==0) return numbers[0];while(left<right){int mid=left+(right-left)/2;if(numbers[mid]>numbers[right])left=mid+1;else if(numbers[mid]<numbers[right])right=mid;elseright--;}return numbers[left];}
};

四、二维数组中的查找

TP
法一：暴力
直接遍历矩阵，判断有没有target

class Solution {
public:bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {for(auto row: matrix){for(auto e: row){if(e==target)return true;}}return false;}
};

时间复杂度：O(MN)
空间复杂度：O(1)

法二：行二分
对二维数组每一行，进行二分查找

class Solution {
public:bool findNumberIn2DArray(vector<vector<int>>& matrix, int t) {if (matrix.size() == 0 || matrix[0].size() == 0) return false;int n = matrix.size(), m = matrix[0].size();int l = 0, r = 0, mid = 0;for (int i = 0; i < n; i ++) {l = 0;r = m - 1;while (l <= r) {mid = l + (r - l) / 2;if (matrix[i][mid] == t) return true;if (matrix[i][mid] < t) l = mid + 1;if (matrix[i][mid] > t) r = mid - 1;}  }return false;}
};

时间复杂度：O(MlogN)
空间复杂度：O(1)

法三：Z字形查找

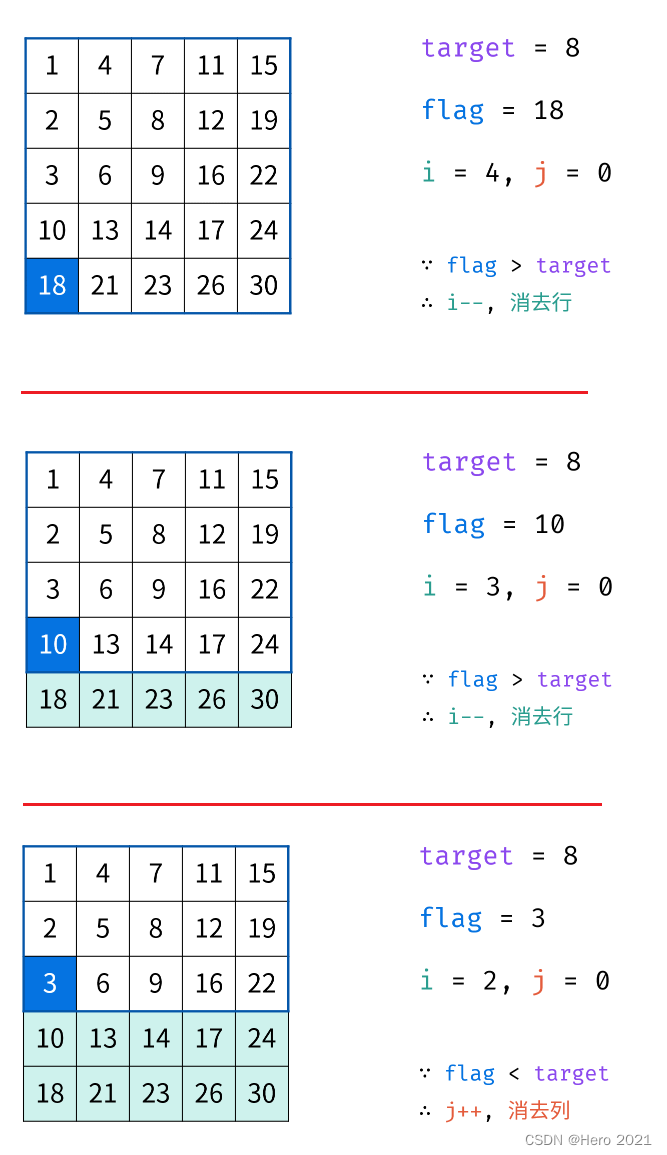
class Solution
{
public:bool findNumberIn2DArray(vector<vector<int>> &matrix, int target){int i = matrix.size() - 1; // 行int j = 0;				   // 列if (matrix.size() == 0 || matrix[0].size() == 0)return false;while (i >= 0 && j <= matrix[0].size() - 1){if (matrix[i][j] > target)i--;else if (matrix[i][j] < target)j++;elsereturn true;}return false;}
};

时间复杂度：O(M+N)
M，N为矩阵的行数和列数
空间复杂度：O(1)