衡水城乡建设局网站长沙seo代理商
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:网格照明
出处:1001. 网格照明
难度
6 级
题目描述
要求
在 n × n \texttt{n} \times \texttt{n} n×n 的二维网格 grid \texttt{grid} grid 上,每个单元格都有一盏灯,最初灯都处于关闭状态。
给你一个二维数组 lamps \texttt{lamps} lamps 表示灯的位置,其中 lamps[i] = [row i , col i ] \texttt{lamps[i] = [row}_\texttt{i}\texttt{, col}_\texttt{i}\texttt{]} lamps[i] = [rowi, coli] 表示打开位于 grid[row i ][col i ] \texttt{grid[row}_\texttt{i}\texttt{][col}_\texttt{i}\texttt{]} grid[rowi][coli] 的灯。即使同一盏灯在数组中出现多次,也是打开这盏灯。
当一盏灯打开时,会照亮自身单元格以及同一行、同一列和两条对角线上的所有其他单元格。
给你另一个二维数组 queries \texttt{queries} queries,其中 queries[j] = [row j , col j ] \texttt{queries[j] = [row}_\texttt{j}\texttt{, col}_\texttt{j}\texttt{]} queries[j] = [rowj, colj]。对于第 j \texttt{j} j 次查询,判断 grid[row j ][col j ] \texttt{grid[row}_\texttt{j}\texttt{][col}_\texttt{j}\texttt{]} grid[rowj][colj] 是否被照亮。在回答第 j \texttt{j} j 次查询之后,关闭位于 grid[row j ][col j ] \texttt{grid[row}_\texttt{j}\texttt{][col}_\texttt{j}\texttt{]} grid[rowj][colj] 的灯和相邻的 8 \texttt{8} 8 盏灯(如果存在)。如果一盏灯和 grid[row j ][col j ] \texttt{grid[row}_\texttt{j}\texttt{][col}_\texttt{j}\texttt{]} grid[rowj][colj] 共享边或角,则这盏灯是相邻的。
返回答案数组 ans \texttt{ans} ans,如果第 j \texttt{j} j 次查询的单元格被照亮,则 ans[j] \texttt{ans[j]} ans[j] 是 1 \texttt{1} 1,否则 ans[j] \texttt{ans[j]} ans[j] 是 0 \texttt{0} 0。
示例
示例 1:
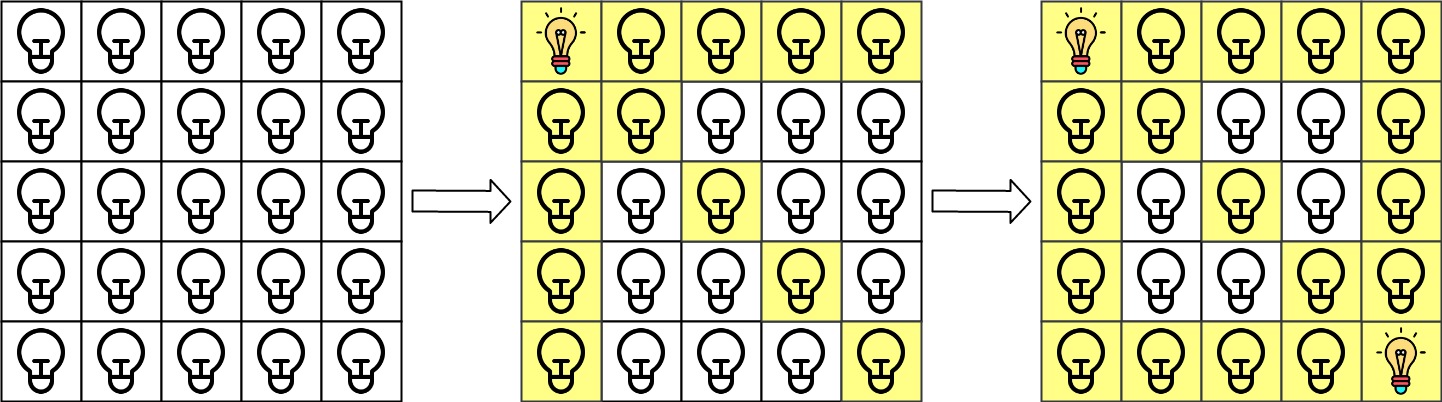
输入: n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]] \texttt{n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]]} n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]]
输出: [1,0] \texttt{[1,0]} [1,0]
解释:最初所有灯都是关闭的。上图中可以看到打开位于 grid[0][0] \texttt{grid[0][0]} grid[0][0] 的灯然后打开位于 grid[4][4] \texttt{grid[4][4]} grid[4][4] 的灯之后的网格。
第 0 \texttt{0} 0 次查询检查 grid[1][1] \texttt{grid[1][1]} grid[1][1] 是否被照亮(蓝色方框)。该单元格被照亮,所以 ans[0] = 1 \texttt{ans[0] = 1} ans[0] = 1。然后,关闭红色方框中的所有灯。
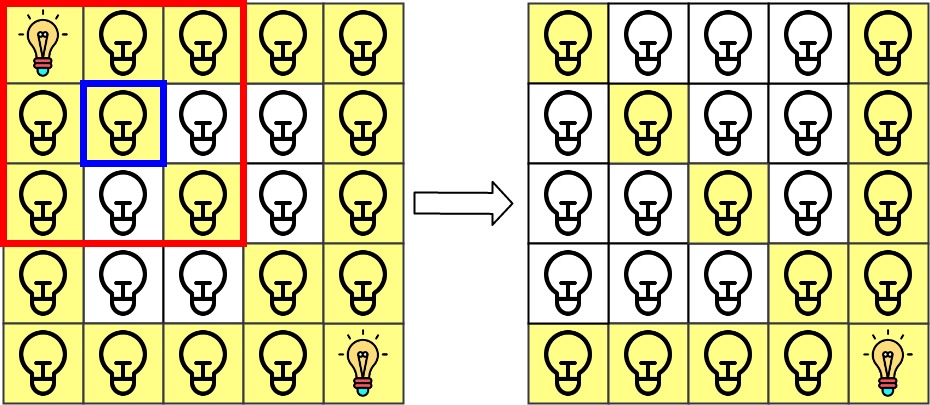
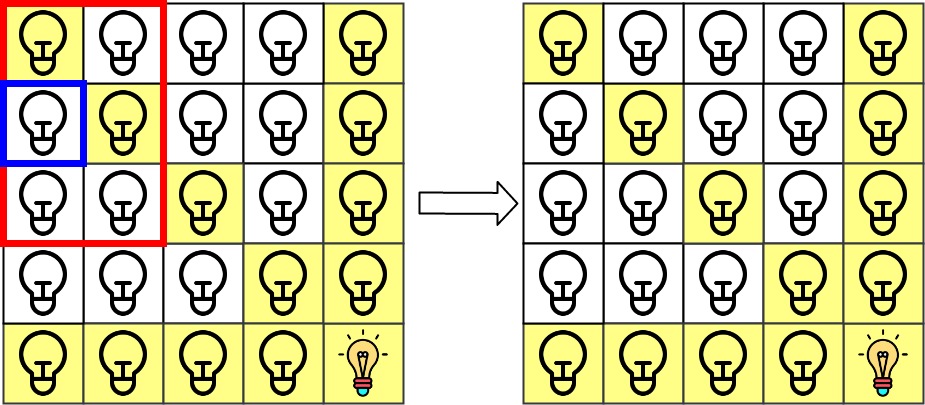
第 1 \texttt{1} 1 次查询检查 grid[1][0] \texttt{grid[1][0]} grid[1][0] 是否被照亮(蓝色方框)。该单元格没有被照亮,所以 ans[1] = 0 \texttt{ans[1] = 0} ans[1] = 0。然后,关闭红色矩形中的所有灯。
示例 2:
输入: n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]] \texttt{n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]]} n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]]
输出: [1,1] \texttt{[1,1]} [1,1]
示例 3:
输入: n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]] \texttt{n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]]} n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]]
输出: [1,1,0] \texttt{[1,1,0]} [1,1,0]
数据范围
- 1 ≤ n ≤ 10 9 \texttt{1} \le \texttt{n} \le \texttt{10}^\texttt{9} 1≤n≤109
- 0 ≤ lamps.length ≤ 20000 \texttt{0} \le \texttt{lamps.length} \le \texttt{20000} 0≤lamps.length≤20000
- 0 ≤ queries.length ≤ 20000 \texttt{0} \le \texttt{queries.length} \le \texttt{20000} 0≤queries.length≤20000
- lamps[i].length = 2 \texttt{lamps[i].length} = \texttt{2} lamps[i].length=2
- 0 ≤ row i , col i < n \texttt{0} \le \texttt{row}_\texttt{i}\texttt{, col}_\texttt{i} < \texttt{n} 0≤rowi, coli<n
- queries[i].length = 2 \texttt{queries[i].length} = \texttt{2} queries[i].length=2
- 0 ≤ row j , col j < n \texttt{0} \le \texttt{row}_\texttt{j}\texttt{, col}_\texttt{j} < \texttt{n} 0≤rowj, colj<n
解法
思路和算法
每个单元格都位于一行、一列和两条对角线上。一个单元格被照亮,等价于至少有一盏打开的灯和该单元格位于同一行、同一列或者同一条对角线上。因此,为了快速判断一个单元格是否被照亮,需要记录每一行、每一列和两个方向的每一条对角线上打开的灯的数量,可以使用哈希表记录。
维护四个哈希表,分别记录每一行打开的灯的数量、每一列打开的灯的数量、每一条方向一对角线上打开的灯的数量和每一条方向二对角线上打开的灯的数量,其中方向一对角线表示从左上到右下方向的对角线,方向二对角线表示从左下到右上方向的对角线。这四个哈希表分别称为行哈希表、列哈希表、对角线一哈希表和对角线二哈希表。
当 0 ≤ row , col < n 0 \le \textit{row}, \textit{col} < n 0≤row,col<n 时,如果位于第 row \textit{row} row 行第 col \textit{col} col 列的灯被打开,则需要将这盏灯存入四个哈希表。
-
由于灯所在的行是 row \textit{row} row,因此在行哈希表中将 row \textit{row} row 对应的数量加 1 1 1;
-
由于灯所在的列是 col \textit{col} col,因此在列哈希表中将 col \textit{col} col 对应的数量加 1 1 1;
-
由于在方向一对角线上,如果向左上移动一步则 row \textit{row} row 和 col \textit{col} col 同时减 1 1 1,如果向右下移动一步则 row \textit{row} row 和 col \textit{col} col 同时加 1 1 1,因此在同一条方向一对角线上的每个单元格满足 row − col \textit{row} - \textit{col} row−col 是定值,在对角线一哈希表中将 row − col \textit{row} - \textit{col} row−col 对应的数量加 1 1 1;
-
由于在方向二对角线上,如果向左下移动一步则 row \textit{row} row 加 1 1 1 且 col \textit{col} col 减 1 1 1,如果向右上移动一步则 row \textit{row} row 减 1 1 1 且 col \textit{col} col 加 1 1 1,因此在同一条方向二对角线上的每个单元格满足 row + col \textit{row} + \textit{col} row+col 是定值,在对角线二哈希表中将 row + col \textit{row} + \textit{col} row+col 对应的数量加 1 1 1。
数组 lamps \textit{lamps} lamps 表示打开的灯的位置。遍历数组 lamps \textit{lamps} lamps,对其中的每一个位置 [ row , col ] [\textit{row}, \textit{col}] [row,col],使用该位置更新四个哈希表。
由于数组 lamps \textit{lamps} lamps 中可能存在重复的位置,因此需要去重,避免同一个位置的灯被重复计算。去重的方法是使用哈希集合存储所有打开的灯的位置,哈希集合可以确保同一个位置只被加入一次。由于每一盏灯所在的行 row \textit{row} row 和列 col \textit{col} col 都是整数且都在范围 [ 0 , n − 1 ] [0, n - 1] [0,n−1] 内,因此可以定义哈希函数 f ( row , col ) = row × n + col f(\textit{row}, \textit{col}) = \textit{row} \times n + \textit{col} f(row,col)=row×n+col,该哈希函数可以确保不同位置对应的哈希值不同。
假设存在位置 [ row 1 , col 1 ] [\textit{row}_1, \textit{col}_1] [row1,col1] 和 [ row 2 , col 2 ] [\textit{row}_2, \textit{col}_2] [row2,col2] 满足 f ( row 1 , col 1 ) = f ( row 2 , col 2 ) f(\textit{row}_1, \textit{col}_1) = f(\textit{row}_2, \textit{col}_2) f(row1,col1)=f(row2,col2),则有 row 1 × n + col 1 = row 2 × n + col 2 \textit{row}_1 \times n + \textit{col}_1 = \textit{row}_2 \times n + \textit{col}_2 row1×n+col1=row2×n+col2,即 ( row 1 − row 2 ) × n = col 2 − col 1 (\textit{row}_1 - \textit{row}_2) \times n = \textit{col}_2 - \textit{col}_1 (row1−row2)×n=col2−col1。由于 ∣ row 1 − row 2 ∣ < n |\textit{row}_1 - \textit{row}_2| < n ∣row1−row2∣<n, ∣ col 2 − col 1 ∣ < n |\textit{col}_2 - \textit{col}_1| < n ∣col2−col1∣<n,且位置都是整数,因此一定有 row 1 − row 2 = col 2 − col 1 = 0 \textit{row}_1 - \textit{row}_2 = \textit{col}_2 - \textit{col}_1 = 0 row1−row2=col2−col1=0, [ row 1 , col 1 ] [\textit{row}_1, \textit{col}_1] [row1,col1] 和 [ row 2 , col 2 ] [\textit{row}_2, \textit{col}_2] [row2,col2] 是相同的位置。
定义哈希函数之后,根据哈希函数计算数组 lamps \textit{lamps} lamps 中的每个位置对应的哈希值。对于每个位置,只有当该位置的哈希值不在哈希集合中时,才将哈希值存入哈希集合,并使用该位置更新四个哈希表。
查询时,对于数组 queries \textit{queries} queries 中的每个位置 [ row , col ] [\textit{row}, \textit{col}] [row,col],首先判断该位置在四个哈希表中对应的数量是否大于 0 0 0,得到查询结果,然后将该位置和全部相邻位置的灯都关闭。具体做法如下。
-
在行哈希表中得到 row \textit{row} row 的数量、在列哈希表中得到 col \textit{col} col 的数量、在对角线一哈希表中得到 row − col \textit{row} - \textit{col} row−col 的数量、在对角线二哈希表中得到 row + col \textit{row} + \textit{col} row+col 的数量,如果该位置在四条线上对应的数量至少有一个大于 0 0 0 则查询结果是 1 1 1,如果该位置在四条线上对应的数量都是 0 0 0 则查询结果是 0 0 0。
-
遍历位置 [ row , col ] [\textit{row}, \textit{col}] [row,col] 和全部相邻位置,对于每个位置,如果该位置对应的哈希值在哈希集合中,则说明该位置的灯处于打开状态,需要关闭,将该位置对应的哈希值从哈希集合中删除,并将该位置在四个哈希表中对应的数量分别减 1 1 1。
查询时的关灯操作可以优化。如果一个单元格所在位置和全部相邻位置中至少有一盏灯打开,则该单元格一定被照亮,因此如果一个单元格没有被照亮,则该单元格所在位置和全部相邻位置的灯一定都处于关闭状态。只有当查询结果是 1 1 1 时,才需要执行关灯操作。
代码
class Solution {public int[] gridIllumination(int n, int[][] lamps, int[][] queries) {Set<Long> set = new HashSet<Long>();Map<Integer, Integer> rowMap = new HashMap<Integer, Integer>();Map<Integer, Integer> columnMap = new HashMap<Integer, Integer>();Map<Integer, Integer> diagonal1Map = new HashMap<Integer, Integer>();Map<Integer, Integer> diagonal2Map = new HashMap<Integer, Integer>();for (int[] lamp : lamps) {int row = lamp[0], column = lamp[1];long position = (long) row * n + column;if (set.add(position)) {rowMap.put(row, rowMap.getOrDefault(row, 0) + 1);columnMap.put(column, columnMap.getOrDefault(column, 0) + 1);int diagonal1 = row - column;diagonal1Map.put(diagonal1, diagonal1Map.getOrDefault(diagonal1, 0) + 1);int diagonal2 = row + column;diagonal2Map.put(diagonal2, diagonal2Map.getOrDefault(diagonal2, 0) + 1);}}int[][] directions = {{0, 0}, {-1, -1}, {-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}};int queriesCount = queries.length;int[] ans = new int[queriesCount];for (int j = 0; j < queriesCount; j++) {int[] query = queries[j];int queryRow = query[0], queryColumn = query[1];boolean flag = rowMap.containsKey(queryRow) || columnMap.containsKey(queryColumn) || diagonal1Map.containsKey(queryRow - queryColumn) || diagonal2Map.containsKey(queryRow + queryColumn);if (flag) {ans[j] = 1;for (int[] direction : directions) {int row = queryRow + direction[0], column = queryColumn + direction[1];int diagonal1 = row - column, diagonal2 = row + column;if (row >= 0 && row < n && column >= 0 && column < n) {long position = (long) row * n + column;if (set.remove(position)) {rowMap.put(row, rowMap.get(row) - 1);if (rowMap.get(row) == 0) {rowMap.remove(row);}columnMap.put(column, columnMap.get(column) - 1);if (columnMap.get(column) == 0) {columnMap.remove(column);}diagonal1Map.put(diagonal1, diagonal1Map.get(diagonal1) - 1);if (diagonal1Map.get(diagonal1) == 0) {diagonal1Map.remove(diagonal1);}diagonal2Map.put(diagonal2, diagonal2Map.get(diagonal2) - 1);if (diagonal2Map.get(diagonal2) == 0) {diagonal2Map.remove(diagonal2);}}}}}}return ans;}
}
复杂度分析
-
时间复杂度: O ( l + q ) O(l + q) O(l+q),其中 l l l 是数组 lamps \textit{lamps} lamps 的长度, q q q 是数组 queries \textit{queries} queries 的长度。需要遍历数组 lamps \textit{lamps} lamps,对于每个打开的灯的位置,将该位置存入哈希集合以及更新四个哈希表的时间都是 O ( 1 ) O(1) O(1),然后需要遍历数组 queries \textit{queries} queries,对于每个查询,计算查询结果以及更新哈希表和哈希集合的时间都是 O ( 1 ) O(1) O(1),因此总时间复杂度是 O ( l + q ) O(l + q) O(l+q)。
-
空间复杂度: O ( l ) O(l) O(l),其中 l l l 是数组 lamps \textit{lamps} lamps 的长度。需要使用四个哈希表记录打开的灯的数量以及使用哈希集合存储打开的灯的位置,哈希表和哈希集合的空间复杂度都是 O ( l ) O(l) O(l)。注意返回值不计入空间复杂度。
