最新免费下载ppt模板网站深圳seo顾问

QR分解

给定一个m×n的矩阵A，其中m≥n，即矩阵A是高矩阵或者是方阵，QR分解将矩阵A分解为两个矩阵Q和R的乘积，其中矩阵Q是一个m×n的各列正交的矩阵，即QTQ=I，矩阵R是一个n×n的上三角矩阵，其对角线元素为正。

如果矩阵A是方阵，且各列线性无关，那么Q是一个正交矩阵，即QTQ=QQT=I。

QR分解有多种算法实现，包括Gram-Schmidt正交化方法、Householder变换方法和Givens旋转方法等，下面我们介绍Gram-Schmidt正交化方法和Householder变换方法，并在MATLAB平台上使用这两种算法来实现QR分解。

Gram-Schmidt算法

对于给定的n维向量a1，a2，……，an，Gram-Schmidt算法可以解决将其标准正交化的问题，即将一个线性无关的向量组转化为一个正交向量组，使得每个向量都与前面的向量正交（垂直），并且可以检验a1，a2，……，an是否是线性相关。

Gram-Schmidt算法的步骤如下：

• 初始化n维向量q1，q2，……，qn，其中q1=a1/||a1||2。
• 对于每个向量ai，i=2：n，进行正交化处理：qi= ai-( q1Tai)q1-…-( qi-1Tai)qi-1。
• 如果qi=0，说明ai是a1，a2，……，ai-1的一个线性组合，可以结束算法了。
• 否则将qi进行单位化，qi=qi/||qi||2。

如果步骤③没有结束，那么说明a1，a2，……，an是线性无关的，而且得到了一个正交向量组q1，q2，……，qn。

Gram-Schmidt算法实现的QR分解

对于给定矩阵A，其列向量线性无关，Gram-Schmidt算法实现的QR分解步骤如下：

• 对列向量a1，a2，……，an按照Gram-Schmidt方法进行正交化。
• 对上一步得到的正交化向量组进行单位化得到各列正交的矩阵Q。
• 根据A=QR，QTQ=I→R=QTA，得到上三角矩阵R

MATLAB验证Gram-Schmidt算法实现QR分解稳定性

通过直观的方法来观察到Gram-Schmidt QR分解的正交性偏差，理论上通过Gram-Schmidt算法后可以得到列向量线性无关的各列正交的矩阵Q，即QTQ=I，我们可以直接计算QTQ，看看计算结果与单位矩阵I的差距

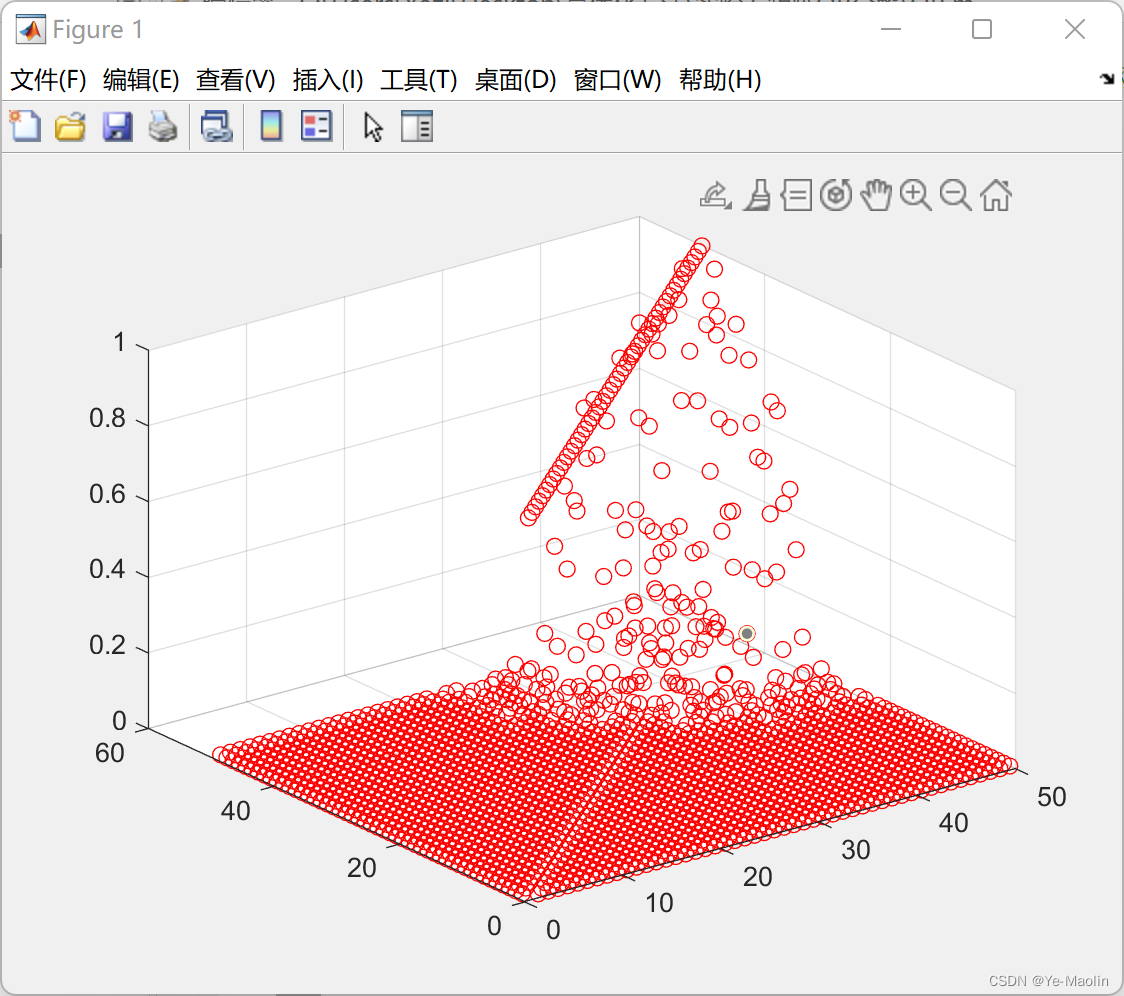
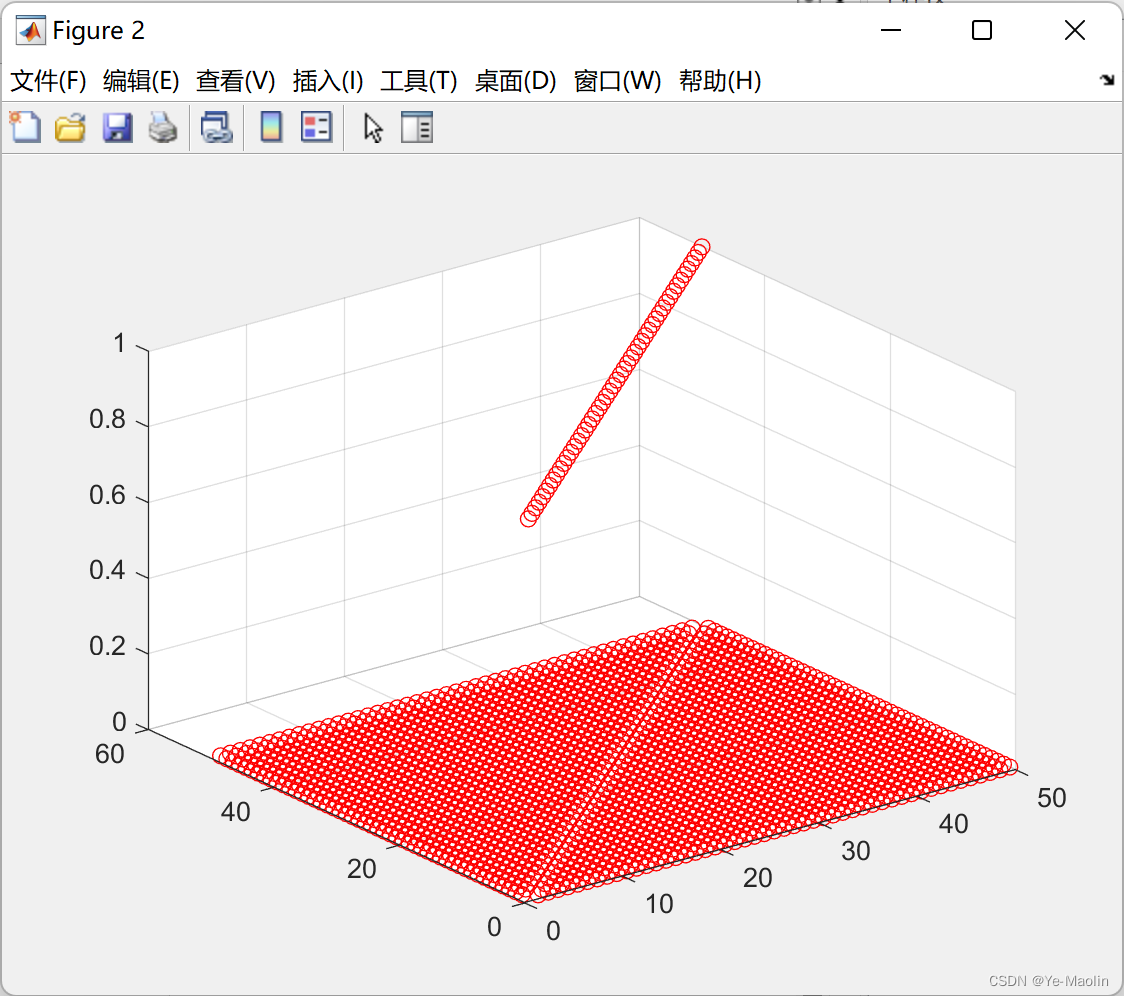
左图是QTQ的计算结果，有图是单位矩阵I，可见由于浮点数存储的舍入误差，随着k增大，积累的误差越大，矩阵Q逐渐失去正交性

clc,clear;
load MatrixA.mat;
[m,n]=size(A);
Q=zeros(m,n);
R=zeros(n,n);
%% Gram-Schmidt QR分解
for k=1:nR(1:k-1,k)=Q(:,1:k-1)'*A(:,k);  %求出R(1,K) - R(K-1,K)v=A(:,k)-Q(:,1:k-1)*R(1:k-1,k); %求出正交化向量qR(k,k)=norm(v);                 %求出R（K,K）Q(:,k)=v/R(k,k);                %单位化向量q
end
%% 正交性偏差
figure(1);
E = zeros(1,n);
for k=2:nmax = 0;for i=1:k-1temp = abs(Q(:,i)' *  Q(:,k));if temp > maxmax = temp;endendE(1,k)=max;
end    
plot(E)
%% 比较QTQ和I
QTQ=Q'*Q;
figure(2);
for i=1:nfor j=1:nscatter3(i,j,QTQ(i,j),'red');hold on;end
end
zlim([0,1]);
I=eye(n);
figure(3);
for i=1:nfor j=1:nscatter3(i,j,I(i,j),'red');hold on;end
end
zlim([0,1]);

Householder变换

Householder变换是一种镜面反射变换，householder变换矩阵为H = I - 2wwT，如何理解这个变换矩阵呢，考虑向量w，那么有：

Hw = (I - 2wwT)w = w - 2w(wTw) = - w

这说明对于平行于w的向量，householder变换的作用是将其反向，再考虑与向量w垂直的向量v，即wTv=0，那么有：

Hv = (I - 2wwT)v = v - 2w(wTv) = v

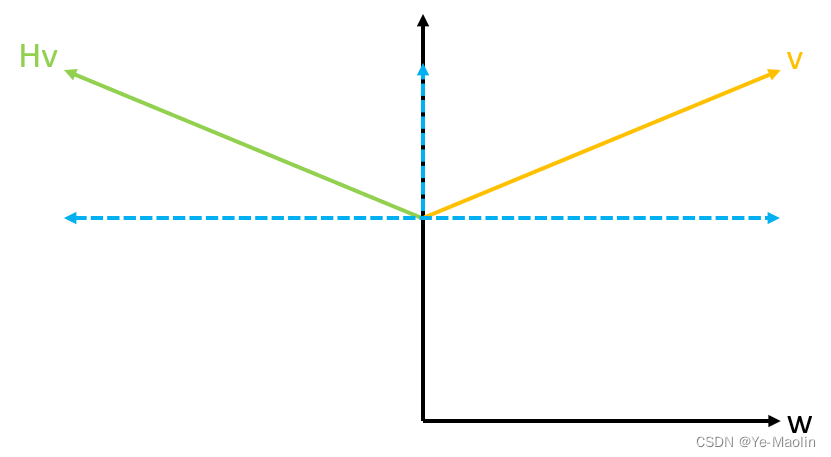
这说明对于垂直于w的向量，householder变换的作用就是对其不起任何作用，那么对于一个普通的向量v来说，平行于w的分量被householder反向，垂直于w的分量不变，那么最终的效果就是将向量v作关于法向量为w的平面的镜像对称

 

基于Householder变换的QR分解

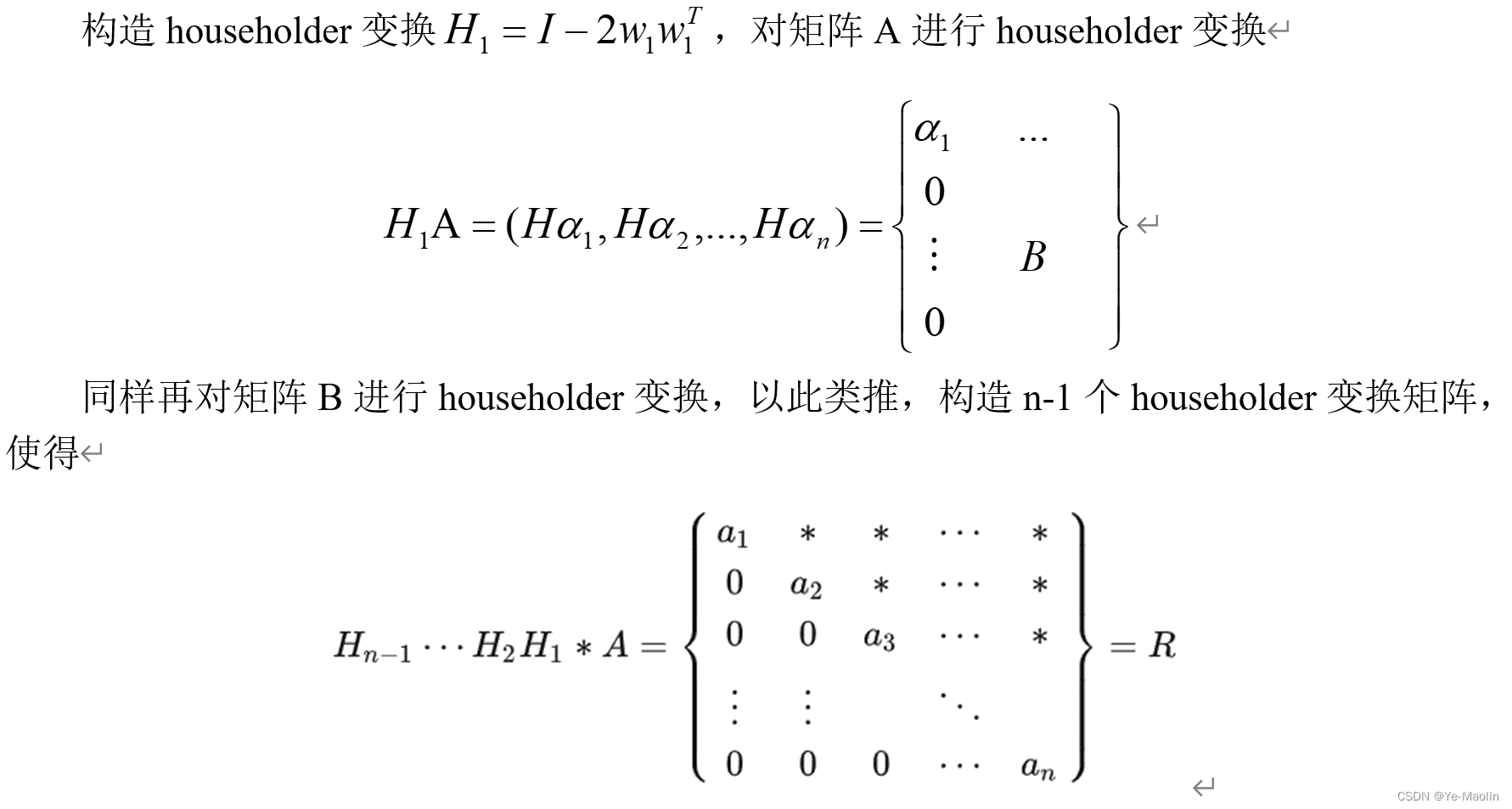
 因为H=H-1，所以A=H1H2,…,Hn-1R，即Q= H1H2,…,Hn-1，再根据A=QR，QTQ=I→R=QTA。

再来比较一下QTQ与单位矩阵I的差距，结果如图所示，左边的是计算出来的QTQ，右边是单位矩阵I

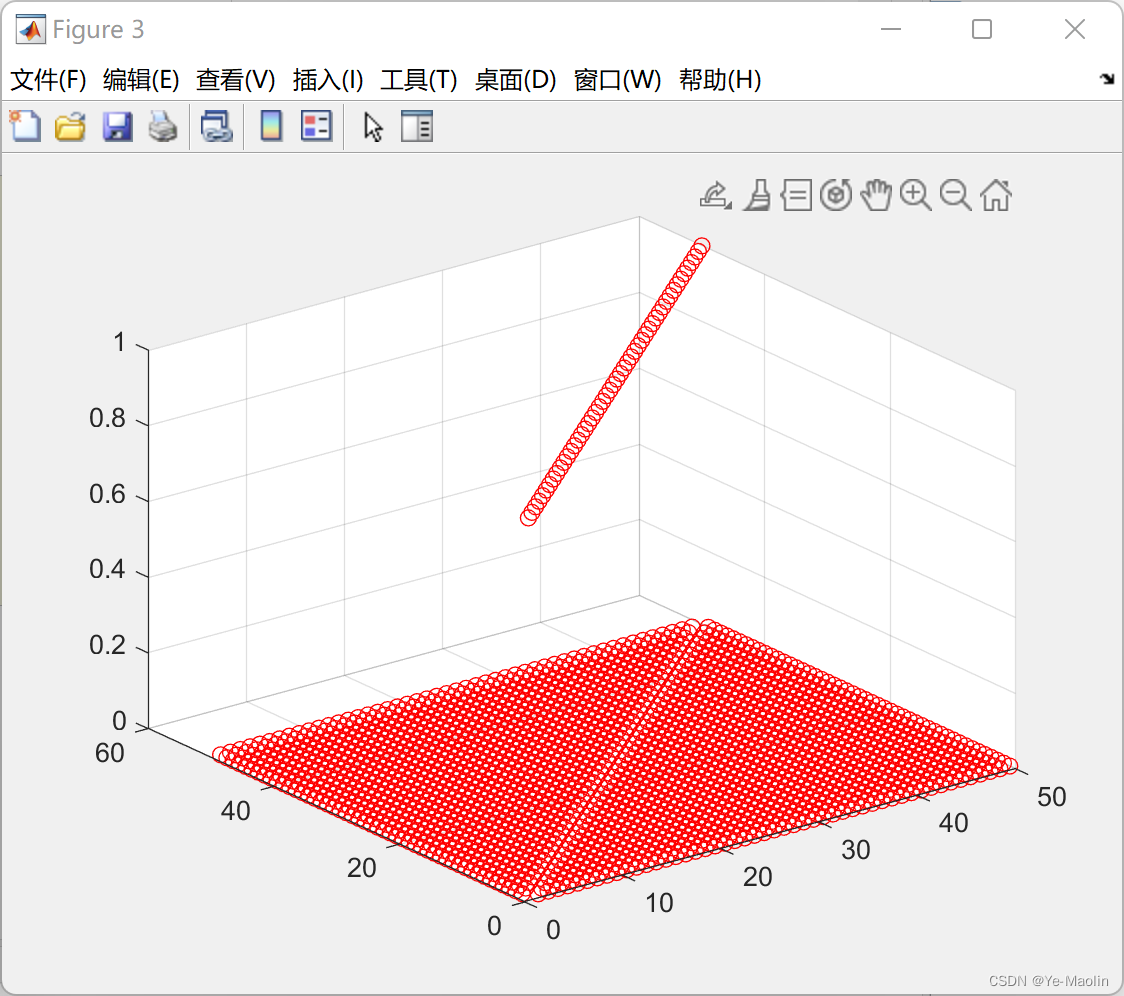
结果QTQ和I基本一样，可见相比其他分解方法，Householder算法能够减小舍入误差的累积，提高计算结果的稳定性。此外，该算法的时间复杂度较低，具备较高的计算效率。

clc,clear;
load MatrixA.mat;
[m,n]=size(A);
Q=zeros(m,n);
R=zeros(n,n);
%% Householder QR分解
[Q,R]=qr(A);    % matlab库函数就是用的Householder
%% 正交性偏差
figure(1);
E = zeros(1,n);
for k=2:nmax = 0;for i=1:k-1temp = abs(Q(:,i)' *  Q(:,k));if temp > maxmax = temp;endendE(1,k)=max;
end    
plot(E)
%% 比较QTQ和I
QTQ=Q'*Q;
figure(2);
for i=1:nfor j=1:nscatter3(i,j,QTQ(i,j),'red');hold on;end
end
zlim([0,1]);
I=eye(n);
figure(3);
for i=1:nfor j=1:nscatter3(i,j,I(i,j),'red');hold on;end
end
zlim([0,1]);

判断矩阵是否可逆

判断矩阵是否可逆有以下几种方法：

• 存在一个矩阵B，使得AB=BA=I，确实可逆。
• 矩阵行列式不为0，可逆。
• 矩阵满秩，可逆。
• 线性方程组Ax=0只有0解，可逆。
• 线性方程组Ax=b只有特解，可逆。

实际上如果一个方阵可以进行QR分解，那么这个方阵也是可逆的。

所以我们直接尝试对矩阵B进行QR分解，如果可以进行QR分解，那么矩阵B可逆。那么我们可以先假设矩阵B是可以进行QR分解，然后我们对矩阵B进行QR分解，显然矩阵B是可以进行QR分解的，这说明矩阵B是可逆的。

求逆

我们之前使用过高斯消元法来求解矩阵的逆，实际上也可以使用QR分解求矩阵的逆。由A = QR，QTQ = I，则A-1 = (QR)-1 = R-1Q-1 = R-1QT。

那么A-1就可以通过R-1QT得到，但是实际上我们并不需要计算R-1，让x= R-1QT，那么我们目标就是要得到x的结果，因为RR-1QT=QT，即Rx=QT，那么我们就需要求解这个线性方程组，由于R是上三角矩阵，所以直接回代就可以求出x，即求出R-1QT，即求出了A-1。

我们先用Gram-Schmidt算法实现的QR分解求解矩阵B的逆，将其与用MATLAB内置的求逆函数结果进行比较，结果如图所示，红色的圆圈是matlab内置的求逆函数计算出来的结果，绿色实心点是我们QR分解求出来的结果，如果二者重合说明计算结果相同。

可以看到基本上绿色的点都和红色的圆圈重合了，可见Gram-Schmidt算法QR分解求逆效果不错。

clc,clear;
load MatrixB.mat;
[m,n]=size(B);
Q=zeros(m,n);
R=zeros(n,n);
%% Gram-Schmidt QR分解
for k=1:nR(1:k-1,k)=Q(:,1:k-1)'*B(:,k);  %求出R(1,K) - R(K-1,K)v=B(:,k)-Q(:,1:k-1)*R(1:k-1,k); %求出正交化向量qR(k,k)=norm(v);                 %求出R（K,K）Q(:,k)=v/R(k,k);                %单位化向量q
end
%% 求逆
inverseQR=R\Q';
inverse=inv(B);
%% 画图比较
for i=0:n-1for j=1:nscatter(i*n+j,inverse(i+1,j),'red');hold on;scatter(i*n+j,inverseQR(i+1,j),'green','.');hold on;end
end

我们再用之前的高斯消元法求解矩阵B的逆，将其与用MATLAB内置的求逆函数结果进行比较，结果如图所示

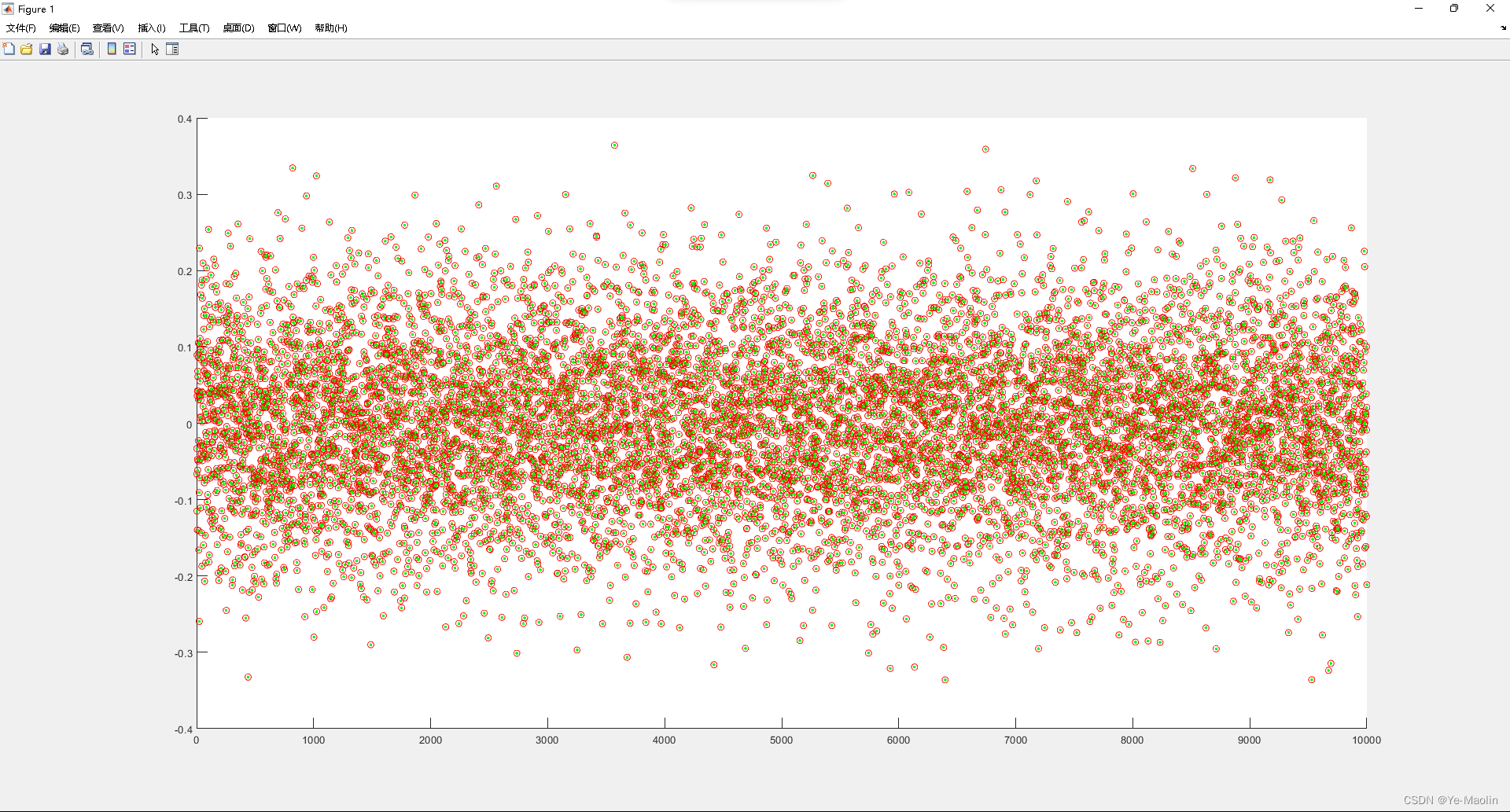
可见高斯消元法求逆的结果也很好，基本上绿色的点都和红色的圆圈重合了。

clc,clear;
load MatrixB.mat;
b=eye(50);
B_b=[B,b];
[n,m]=size(B_b);
for i=1:nfor j=m:-1:iB_b(i,j)=B_b(i,j)/B_b(i,i);endfor j=i+1:nfor k=m:-1:iB_b(j,k)=B_b(j,k)-B_b(j,i)*B_b(i,k);endend
%     fprintf('第%d次消元\n',i);
%     disp(rats(A_b));
end
for i=n-1:-1:1for j=i:-1:1for k=m:-1:n+1B_b(j,k)=B_b(j,k)-B_b(j,i+1)*B_b(i+1,k);endB_b(j,i+1)=0;end
%     fprintf('第%d次回代\n',n-i);
%     disp(rats(A_b));
end
gaussInverse=B_b(:,end-49:end);
inverse=inv(B);
%% 画图比较
for i=0:n-1for j=1:nscatter(i*n+j,inverse(i+1,j),'red');hold on;scatter(i*n+j,gaussInverse(i+1,j),'green','.');hold on;end
end

再用householder算法实现的QR分解求解矩阵B的逆，将其与用MATLAB内置的求逆函数结果进行比较，结果如图所示。

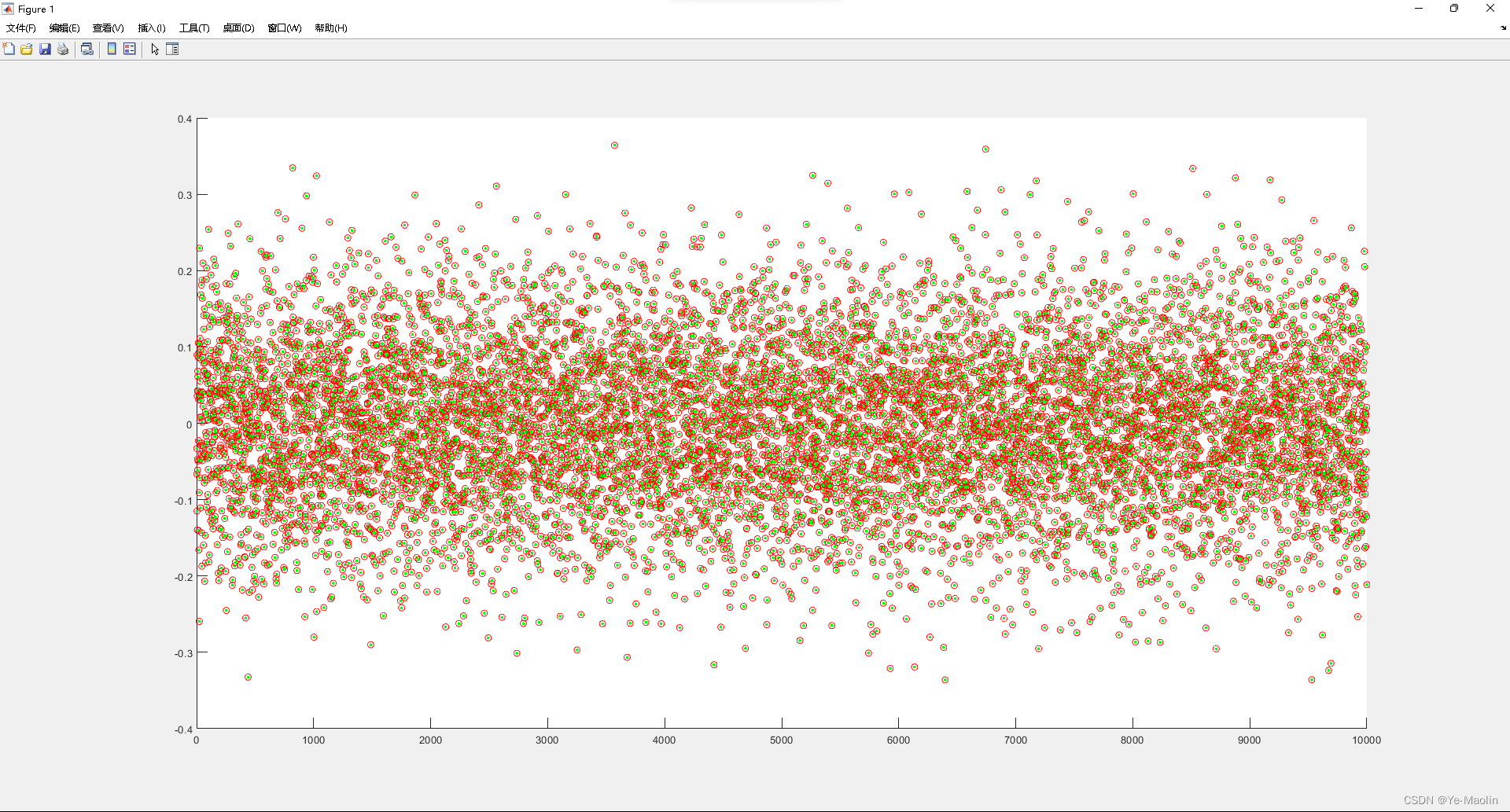
可见householder实现的QR分解求逆结果效果很好，基本上和matlab内置求逆函数结果相同，速度上也不慢。

clc,clear;
load MatrixB.mat;
[m,n]=size(B);
Q=zeros(m,n);
R=zeros(n,n);
%% Householder QR分解
[Q,R]=qr(B);    % matlab库函数就是用的Householder
%% 求逆
inverseQR=R\Q';
inverse=inv(B);
%% 画图比较
for i=0:n-1for j=1:nscatter(i*n+j,inverse(i+1,j),'red');hold on;scatter(i*n+j,inverseQR(i+1,j),'green','.');hold on;end
end