淄博网站制作设计公司网页模板素材

问题定义

强化学习关注的是在于环境交互中学习，是一种试错学习的范式。在正式进入强化学习之前，我们先来了解多臂老虎机问题。该问题也被看作简化版的强化学习，帮助我们更快地过度到强化学习阶段。

有一个拥有 $K$ 根拉杆的老虎机，拉动每根拉杆都有着对应奖励 $R$，且这些奖励可以进行累加。在各根拉杆的奖励分布未知的情况下，从头开始尝试，在进行 $T$ 步操作次数后，得到尽可能高的累计奖励。

对于每个动作 $a$，我们定义其期望奖励是 $Q(a)$。是，至少存在一根拉杆，它的期望奖励不小于拉动其他任意一根拉杆，我们将该最优期望奖励表示为
$$Q^{\ast }=\underset{a\in A}{\max }Q(a)$$
为了更为直观的表示实际累计奖励和真实累计奖励之间的误差，我们引入懊悔概念，用来表示它们之间的差值。
$$R(a)=Q^{\ast }-Q(a)$$

下面我们编写代码来实现一个拉杆数为 10 的多臂老虎机。其中拉动每根拉杆的奖励服从伯努利分布（Bernoulli distribution），即每次拉下拉杆有的概率获得的奖励为 1，有的概率获得的奖励为 0。奖励为 1 代表获奖，奖励为 0 代表没有获奖。

import numpy as np
import matplotlib.pyplot as plt
class BernouliiBandit:def __init__(self, K):self.probs:np.ndarray = np.random.uniform(size=K)  # type: ignore # 随机生成K个0～1的数,作为拉动每根拉杆的获奖 ## 概率self.best_idx = np.argmax(self.probs)  # 获奖概率最大的拉杆self.best_prob = self.probs[self.best_idx]  # 最大的获奖概率self.K = Kdef step(self, k):if np.random.rand() < self.probs[k]:return 1else:return 0

接下来我们用一个 Solver 基础类来实现上述的多臂老虎机的求解方案。

class Solver:def __init__(self, bandit) -> None:self.bandit = banditself.counts = np.zeros(self.bandit.K)self.regret = 0self.actions = []self.regrets = []def update_regret(self, k):self.regret += self.bandit.best_prob - self.bandit.probs[k]self.regrets.append(self.regret)def run_one_step(self):return NotImplementedErrordef run(self, num_steps):for _ in range(num_steps):k:int = self.run_one_step() #type:ignoreself.counts[k] += 1self.actions.append(k)self.update_regret(k)

解决方法

这个问题的难度在于探索和利用的平衡。一个最简单的策略就是一直选择第 $k$ 根拉杆，但这样太依赖运气，万一是最差的一根，就会死翘翘；或者每次都随机选，这种方式只可能得到平均期望，而不会得到最优期望。因此探索和利用要相互权衡才有可能得到最好的结果。

贪心算法

完全贪婪算法即在每一时刻采取期望奖励估值最大的动作（拉动拉杆），这就是纯粹的利用，而没有探索，所以我们通常需要对完全贪婪算法进行一些修改，其中比较经典的一种方法为 $ϵ$ -Greedy 算法。 $ϵ$ -Greedy 在完全贪婪算法的基础上添加了噪声，每次以概率 $ϵ$ 选择以往经验中期望奖励估值最大的那根拉杆（利用），以概率 $ϵ$ 随机选择一根拉杆（探索）

class EpsilonGreedy(Solver):def __init__(self, bandit, epsilon=0.1, init_prob=1.0):super(EpsilonGreedy, self).__init__(bandit)self.epsilon = epsilonself.estimates = np.array([init_prob]*self.bandit.K)def run_one_step(self):if np.random.random() < self.epsilon:k = np.random.randint(0, self.bandit.K)else:k = np.argmax(self.estimates)r = self.bandit.step(k)self.estimates[k] += 1.0/(self.counts[k] + 1) * (r - self.estimates[k])return k

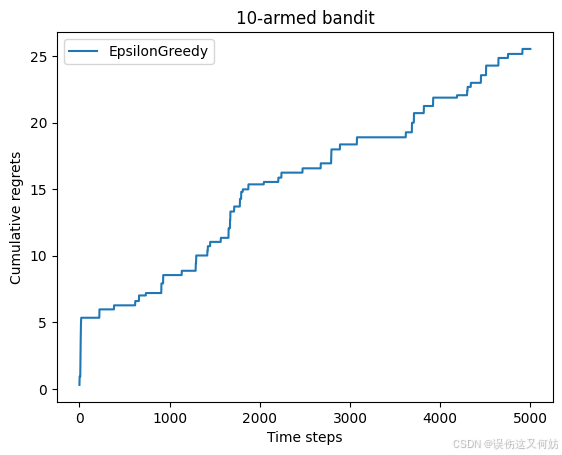
为了更加直观的展示，可以把每一时间步的累积函数绘制出来。

def plot_results(solvers, solver_names):for idx, solver in enumerate(solvers):time_list = range(len(solver.regrets))plt.plot(time_list, solver.regrets, label=solver_names[idx])plt.xlabel('Time steps')plt.ylabel('Cumulative regrets')plt.title('%d-armed bandit' % solvers[0].bandit.K)plt.legend()plt.show()np.random.seed(1)
epsilon_greedy_solver = EpsilonGreedy(bandit_10_arm, epsilon=0.01)
epsilon_greedy_solver.run(5000)
print('epsilon-贪婪算法的累积懊悔为：', epsilon_greedy_solver.regret)
plot_results([epsilon_greedy_solver], ["EpsilonGreedy"])

上置信界算法

上置信界算法是一种经典的基于不确定性的策略算法，它的思想用到了一个非常著名的数学原理：霍夫丁不等式。

在霍夫丁不等式中，令 $(X_1,\dots ,X_n)$ 为 $n$ 个独立同分布的随机变量，取值范围为 ([0,1])，其经验期望为：

$${\bar{x}}_n=\frac{1}{n}\sum _{j=1}^n{X}_j$$

则有：

P { E [ X ] ≥ x ˉ n + u } ≤ e − 2 n u 2 \mathbb{P} \left\{ \mathbb{E}[X] \geq \bar{x}_n + u \right\} \leq e^{-2nu^2} P{E[X]≥xˉn​+u}≤e−2nu2

class UCB(Solver):def __init__(self, bandit, init_prob, coef):super(UCB, self).__init__(bandit)self.total_count = 0self.estimates = np.array([init_prob*1.0]*self.bandit.K)self.coef = coefdef run_one_step(self):self.total_count += 1ucb = self.estimates + self.coef * np.sqrt(np.log(self.total_count) / (2 * (self.counts + 1)))k = np.argmax(ucb)r = self.bandit.step(k)self.estimates[k] += (r - self.estimates[k]) / (self.counts[k] + 1)return k
np.random.seed(1)
UCB_solver = UCB(bandit_10_arm, 1, 1)
UCB_solver.run(5000)
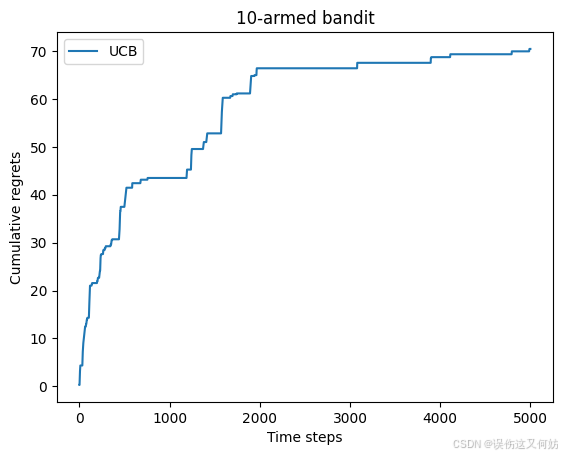
print('上置信界算法的累积懊悔为：', UCB_solver.regret)
plot_results([UCB_solver], ["UCB"])

汤普森采样

先假设拉动每根拉杆的奖励服从一个特定的概率分布，然后根据拉动每根拉杆的期望奖励来进行选择。但是由于计算所有拉杆的期望奖励的代价比较高，汤普森采样算法使用采样的方式，即根据当前每个动作 的奖励概率分布进行一轮采样，得到一组各根拉杆的奖励样本，再选择样本中奖励最大的动作。可以看出，汤普森采样是一种计算所有拉杆的最高奖励概率的蒙特卡洛采样方法。

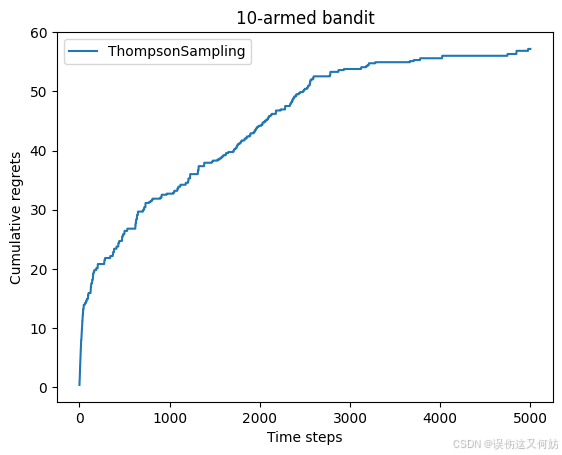
class ThompsonSampling(Solver):def __init__(self, bandit) -> None:super(ThompsonSampling, self).__init__(bandit)self._a = np.ones(self.bandit.K)self._b = np.ones(self.bandit.K)def run_one_step(self):samples = np.random.beta(self._a, self._b)k = np.argmax(samples)r = self.bandit.step(k)self._a[k] += rself._b[k] += (1-r)return knp.random.seed(1)
thompson_sampling_solver = ThompsonSampling(bandit_10_arm)
thompson_sampling_solver.run(5000)
print('汤普森采样算法的累积懊悔为：', thompson_sampling_solver.regret)
plot_results([thompson_sampling_solver], ["ThompsonSampling"])