常州网站seo代理加盟福州seo推广服务
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:两球之间的磁力
出处:1552. 两球之间的磁力
难度
5 级
题目描述
要求
在代号为地球 C-137 的世界中,Rick 发现如果他将两个球放在他新发明的篮子中,它们之间会形成特殊形式的磁力。Rick 有 n \texttt{n} n 个空的篮子,第 i \texttt{i} i 个篮子的位置在 position[i] \texttt{position[i]} position[i],Morty 想把 m \texttt{m} m 个球放到这些篮子中,使得任意两球间的最小磁力最大。
Rick 声明,两个位于 x \texttt{x} x 和 y \texttt{y} y 的球之间的磁力为 |x - y| \texttt{|x - y|} |x - y|。
给定一个整数数组 position \texttt{position} position 和一个整数 m \texttt{m} m,返回最小磁力的最大值。
示例
示例 1:
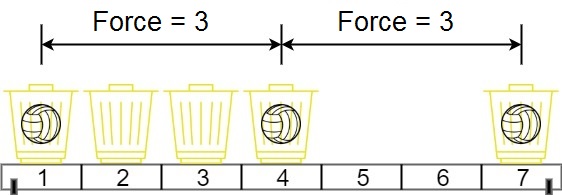
输入: position = [1,2,3,4,7], m = 3 \texttt{position = [1,2,3,4,7], m = 3} position = [1,2,3,4,7], m = 3
输出: 3 \texttt{3} 3
解释:将 3 \texttt{3} 3 个球分别放入位于 1 \texttt{1} 1、 4 \texttt{4} 4 和 7 \texttt{7} 7 的三个篮子,两球间的磁力分别为 [3, 3, 6] \texttt{[3, 3, 6]} [3, 3, 6]。最小磁力为 3 \texttt{3} 3。我们无法让最小磁力大于 3 \texttt{3} 3。
示例 2:
输入: position = [5,4,3,2,1,1000000000], m = 2 \texttt{position = [5,4,3,2,1,1000000000], m = 2} position = [5,4,3,2,1,1000000000], m = 2
输出: 999999999 \texttt{999999999} 999999999
解释:我们使用位于 1 \texttt{1} 1 和 1000000000 \texttt{1000000000} 1000000000 的篮子时最小磁力最大。
数据范围
- n = position.length \texttt{n} = \texttt{position.length} n=position.length
- 2 ≤ n ≤ 10 5 \texttt{2} \le \texttt{n} \le \texttt{10}^\texttt{5} 2≤n≤105
- 1 ≤ position[i] ≤ 10 9 \texttt{1} \le \texttt{position[i]} \le \texttt{10}^\texttt{9} 1≤position[i]≤109
- 所有 position \texttt{position} position 中的整数各不相同
- 2 ≤ m ≤ position.length \texttt{2} \le \texttt{m} \le \texttt{position.length} 2≤m≤position.length
解法
思路和算法
由于两个球之间的磁力等于两个球之间的距离,因此为了得到最小磁力,需要计算最小距离。以下将最小磁力的最大值对应的最小距离的最大值称为「临界距离」。
当 m m m 个球已经放入篮子时,最小距离一定是其中一对位置相邻的球之间的距离,因此需要将数组 position \textit{position} position 升序排序,在排序后的篮子位置之间计算放入的球的最小距离。
如果任意两个球之间的距离不超过临界距离,则可以放入至少 m m m 个球;如果存在两个球之间的距离大于临界距离,则不能放入 m m m 个球。因此,这道题是二分查找判定问题,需要找到可以放入 m m m 个球的最小距离的最大值。
用 low \textit{low} low 和 high \textit{high} high 分别表示二分查找的下界和上界。由于至少需要放入两个球,当最小距离最大时每个球放在不同的篮子中,因此 low \textit{low} low 的初始值等于 1 1 1;由于最大距离为两端的篮子之间的距离,因此 high \textit{high} high 的初始值等于 position \textit{position} position 中的最大值与最小值之差。
为了能放入 m m m 个球,当最小距离确定时,应该在确保相邻的球之间的距离不小于最小距离的前提下尽可能放入更多的球。因此,第一个球应该放到最左边的篮子中,后面的每个球应该放到与前一个球的距离大于等于最小距离的最近的篮子中。根据该规则,遍历排序后的数组 position \textit{position} position,判断每个球应该放到哪些篮子中,并计算放到篮子中的球的总数。
每次查找时,取 mid \textit{mid} mid 为 low \textit{low} low 和 high \textit{high} high 的平均数向上取整,将 mid \textit{mid} mid 作为最小距离,判断是否可以将 m m m 个球放到篮子中,执行如下操作。
-
如果最小距离是 mid \textit{mid} mid 时可以将 m m m 个球放到篮子中,则临界距离大于等于 mid \textit{mid} mid,因此在 [ mid , high ] [\textit{mid}, \textit{high}] [mid,high] 中继续查找。
-
如果最小距离是 mid \textit{mid} mid 时不能将 m m m 个球放到篮子中,则临界距离小于 mid \textit{mid} mid,因此在 [ low , mid − 1 ] [\textit{low}, \textit{mid} - 1] [low,mid−1] 中继续查找。
当 low = high \textit{low} = \textit{high} low=high 时,查找结束,此时 low \textit{low} low 即为临界距离。
得到临界距离之后,临界距离对应的磁力即为最小磁力的最大值。
代码
class Solution {public int maxDistance(int[] position, int m) {Arrays.sort(position);int n = position.length;int low = 1, high = position[n - 1] - position[0];while (low < high) {int mid = low + (high - low + 1) / 2;if (canPutMBalls(position, m, mid)) {low = mid;} else {high = mid - 1;}}return low;}public boolean canPutMBalls(int[] position, int m, int force) {int count = 1;int prev = position[0];int n = position.length;for (int i = 1; i < n; i++) {if (position[i] - prev >= force) {count++;if (count == m) {return true;}prev = position[i];}}return false;}
}
复杂度分析
-
时间复杂度: O ( n log ( n p ) ) O(n \log (np)) O(nlog(np)),其中 n n n 是数组 position \textit{position} position 的长度, p p p 是数组 position \textit{position} position 中的最大值。排序需要 O ( n log n ) O(n \log n) O(nlogn) 的时间,排序之后需要执行 O ( log p ) O(\log p) O(logp) 次二分查找,每次二分查找需要 O ( n ) O(n) O(n) 的时间遍历数组 position \textit{position} position 判断是否可以将 m m m 个球放到篮子中,二分查找共需要 O ( n log p ) O(n \log p) O(nlogp) 的时间,因此时间复杂度是 O ( n log n + n log p ) = O ( n log ( n p ) ) O(n \log n + n \log p) = O(n \log (np)) O(nlogn+nlogp)=O(nlog(np))。
-
空间复杂度: O ( log n ) O(\log n) O(logn),其中 n n n 是数组 position \textit{position} position 的长度。排序需要 O ( log n ) O(\log n) O(logn) 的递归调用栈空间。
