当前位置：首页 > news >正文

怎么做通知维护网站网上哪里可以免费打广告

news 2025/7/4 22:49:48

怎么做通知维护网站,网上哪里可以免费打广告,海珠区新闻,网站备案承若怎么写目录一、树 1.什么是树 2. 与树相关的概念二、二叉树 1.什么是二叉树 2.二叉树特点 3.满二叉树与完全二叉树 4.二叉树性质相关题目： 5.二叉树的存储 6.二叉树的遍历和基本操作二叉树的遍历二叉树的基本操作一、树 1.什么是树子树是不相交的;…

一、树

1.什么是树

2. 与树相关的概念

二、二叉树

1.什么是二叉树

2.二叉树特点

3.满二叉树与完全二叉树

4.二叉树性质

一、树

1.什么是树

子树是不相交的;
除了根结点外，每个结点有且仅有一个父结点
一棵N个结点的树有N-1条边。

树： 非树：

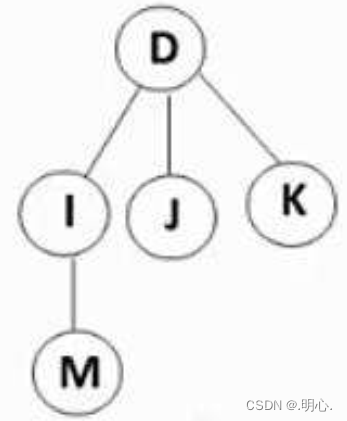
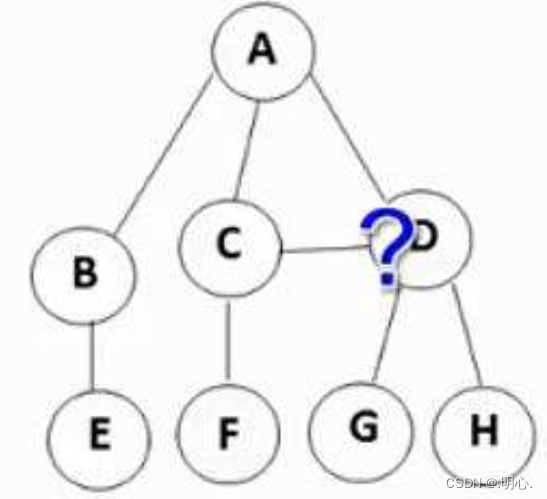
2. 与树相关的概念

结点的度：一个结点含有子树的个数称为该结点的度；如上图：A的度为6
树的度：一棵树中，所有结点度的最大值称为树的度；如上图：树的度为6
叶子结点或终端结点：度为0的结点称为叶结点；如上图：B、C、H、I...等节点为叶结点
双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点；如上图：A是B的父结点
孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点；如上图：B是A的孩子结点
根结点：一棵树中，没有双亲结点的结点；如上图：A
结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推
树的高度或深度：树中结点的最大层次；如上图：树的高度为4

二、二叉树

1.什么是二叉树

一棵二叉树是结点的一个有限集合，该集合：

或者为空
或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。

2.二叉树特点

二叉树不存在度大于2的结点（树的度：一棵树中，所有结点度的最大值称为树的度）
二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

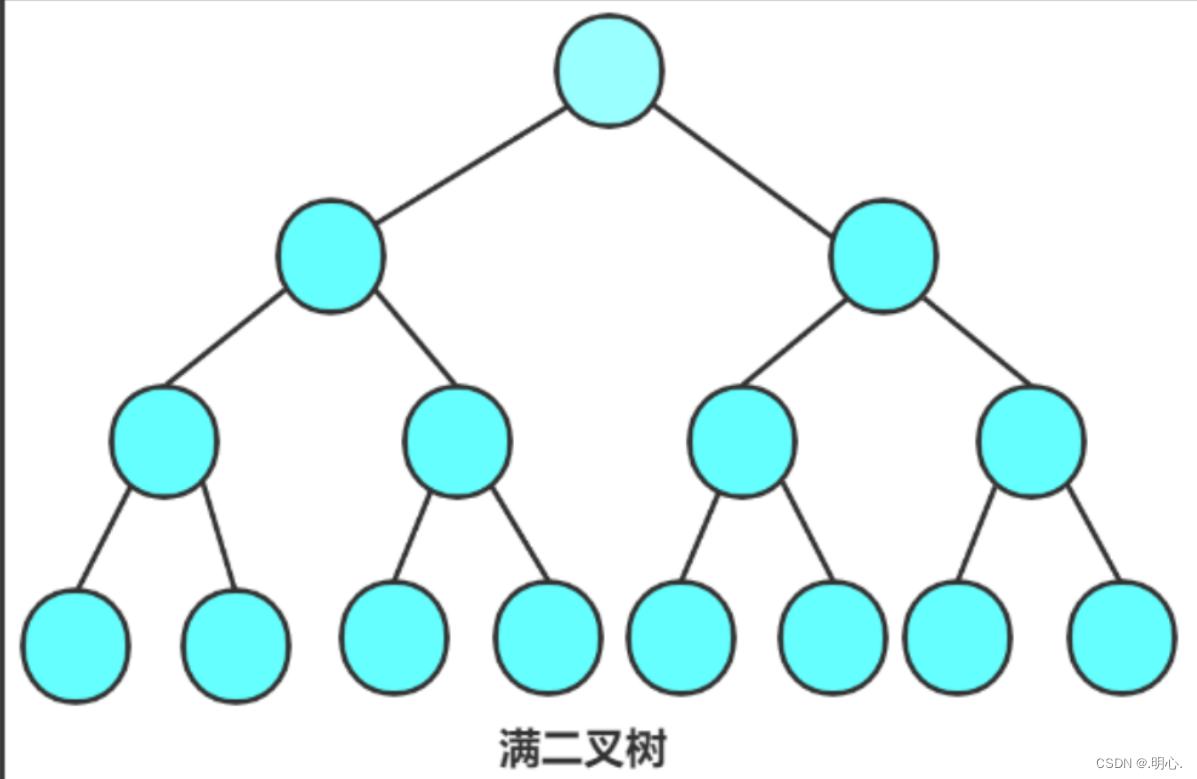
3.满二叉树与完全二叉树

满二叉树: 一棵二叉树，如果每层的结点数都达到最大值，则这棵二叉树就是满二叉树。也就是说，如果一棵又树的层数为K，且结点总数是2^k-1，则它就是满二叉树

完全二叉树: 完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 意思就是完全二叉树的所有节点从上到下，从左到右依次排满。要注意的是满二叉树是一种特殊的完全二又树。

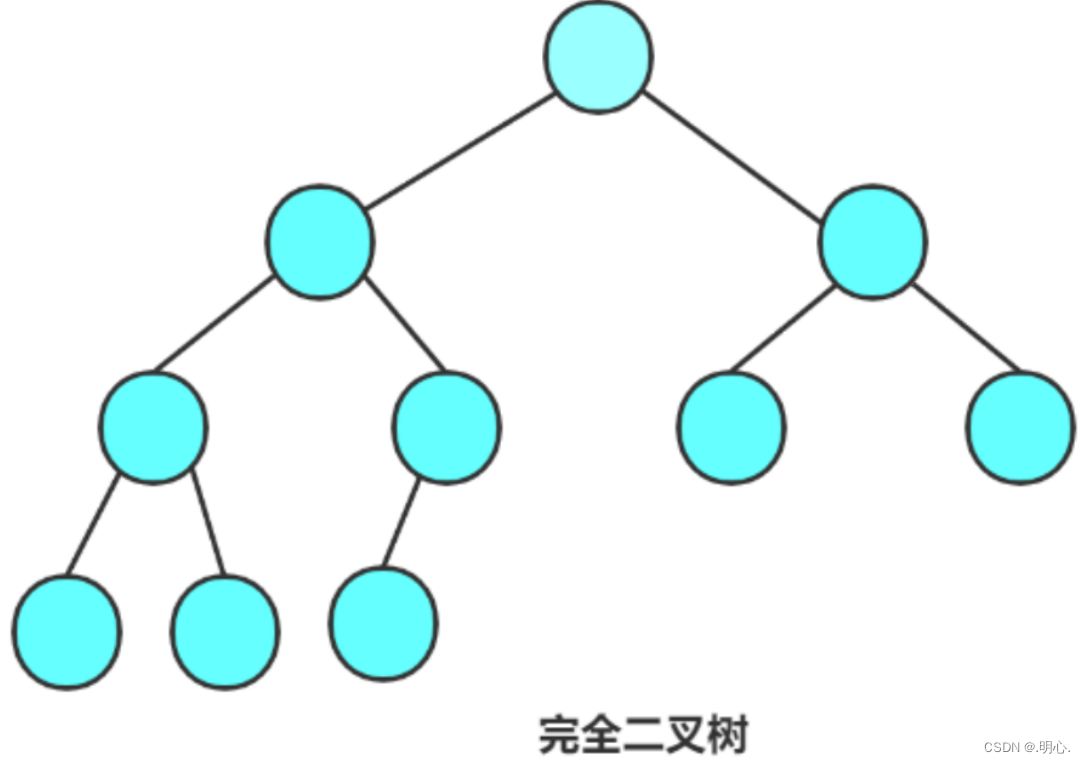
完全二叉树有一个特点，那就是如果总结点数为奇数，那么这个二叉树就只有一个度为1的节点，如果是偶数，就没有度为1的结点。

4.二叉树性质

1. 若规定根结点的层数为1，则一棵非空二叉树的第i层上最多有 $2^{i}-1$ (i>0)个结点

2. 若规定只有根结点的二叉树的深度为1，则深度为K的二叉树的最大结点数是 $2^{k}-1$ (k>=0)

3. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0＝n2＋1

4. 具有n个结点的完全二叉树的深度k为 $\log _{_{2}}(n+1)$ 上取整

5. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为i 的结点有：

若i>0，双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点
若2i+1<n，左孩子序号：2i+1，否则无左孩子
若2i+2<n，右孩子序号：2i+2，否则无右孩子

5.二叉树的存储

二叉树的存储结构分为：
顺序存储和类似于链表的链式存储。二叉树的链式存储是通过一个一个的节点引用起来的，常见的表示方式有二叉和三叉表示方式（孩子表示法以及孩子双亲表示法）。

// 孩子表示法
class Node {int val; // 数据域Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
} 
// 孩子双亲表示法
class Node {int val; // 数据域Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树Node parent; // 当前节点的根节点
}

6.二叉树的遍历和基本操作

二叉树的遍历

1.前中后序遍历

前序遍历：根节点左子树右子树
中序遍历：左子树根节点右子树
后序遍历：左子树右子树根节点

2.层序遍历

自上而下，自左至右逐层访问树的结点的过程就是层序遍历

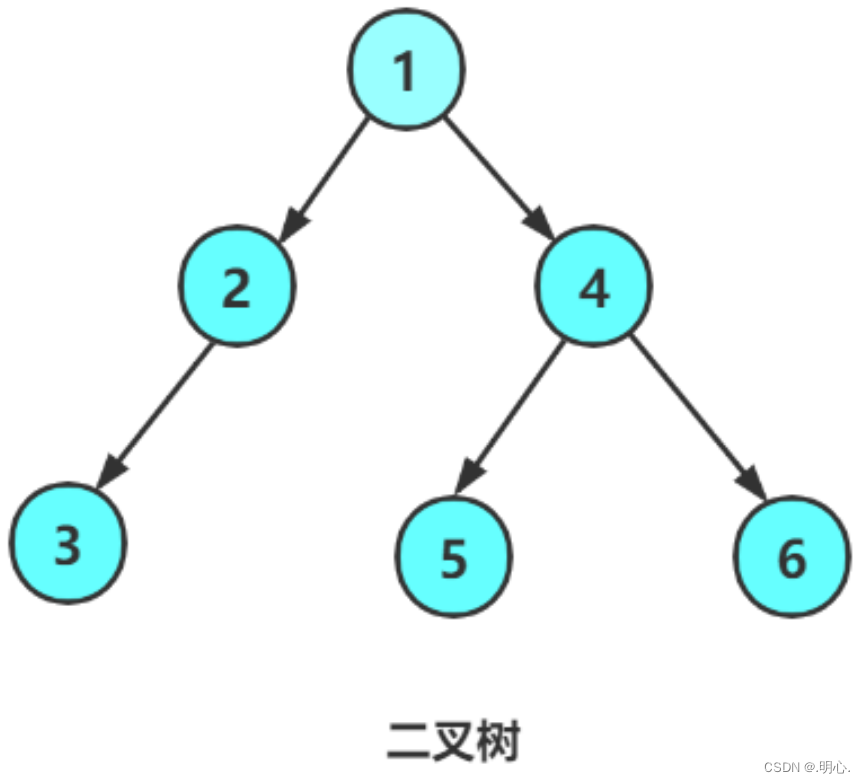
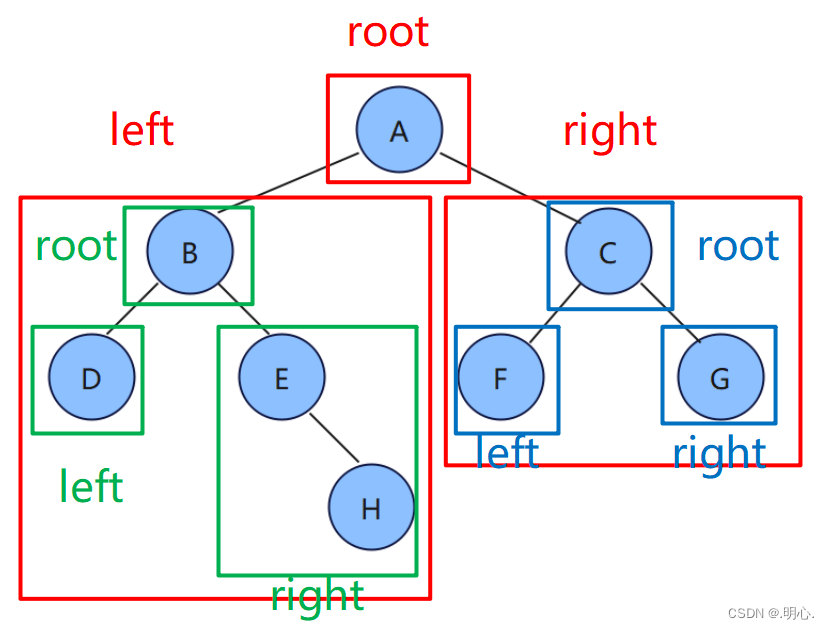
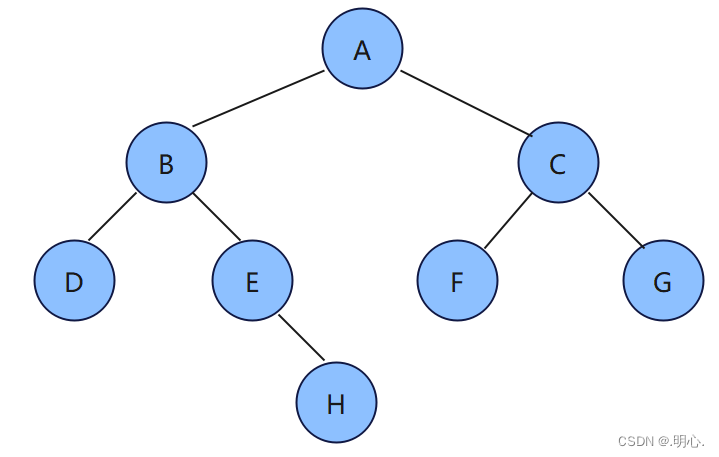
有如下二叉树，大家可用上述方法自行遍历

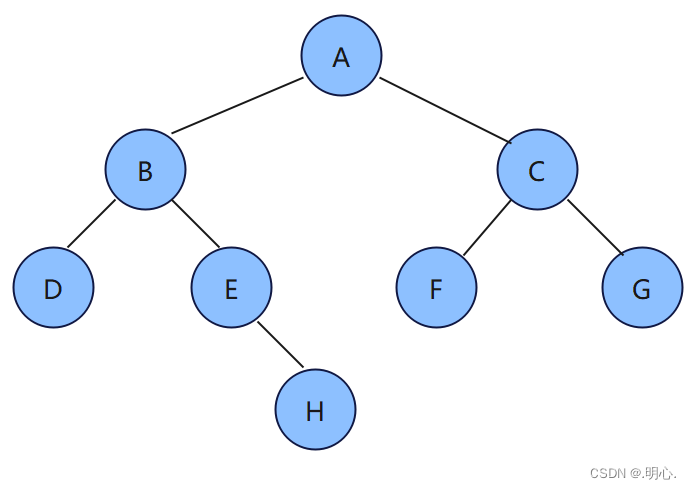
前序遍历:A B D E H C F G

中序遍历:D B E H A F C G

后序遍历:B D E H C F G A

层序遍历:A B C D E F G H

代码实现：

这里先按照上图用穷举的方式快速构建一颗二叉树（不是构建二叉树的正确方法）

public class BinaryTree {public static class TreeNode {TreeNode left;TreeNode right;char val;TreeNode(char val) {this.val = val;}}private TreeNode root;public TreeNode createTree() {TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');root = A;A.left = B;A.right = C;B.left = D;B.right = E;C.left = F;C.right = G;E.right = H;return A;}//前序遍历public void preOrder(TreeNode root){if(root==null){return;}System.out.print(root.val+" ");preOrder(root.left);preOrder(root.right);}//中序遍历public void inOrder(TreeNode root){if (root==null){return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}//后序遍历public void postOrder(TreeNode root){if (root==null){return;}preOrder(root.left);preOrder(root.right);System.out.print(root.val+" ");}}

public class Main {public static void main(String[] args) {BinaryTree binaryTree=new BinaryTree();BinaryTree.TreeNode root=binaryTree.createTree();System.out.print("前序遍历:");binaryTree.preOrder(root);System.out.println();System.out.print("中序遍历:");binaryTree.inOrder(root);System.out.println();System.out.print("后序遍历:");binaryTree.postOrder(root);}
}

运行结果：

二叉树的基本操作

1. 获取树中节点的个数

这个方法实现在这里有两种思路：

1.遍历这个树，是结就nodeSize++
2.用子问题的思路来解决：总结点数=左子树结点的个数+右子树结点的个数+根结点

    public static int nodeSize=0;//获取树中节点的个数(遍历每个节点）public void size(TreeNode root){if (root==null){return;}nodeSize++;size(root.left);size(root.right);}//用子问题的思路来解决：总节点数=左子树节点的个数+右子树节点的个数+根节点public int size2(TreeNode root){if (root==null){return 0;}int tmp=size2(root.left)+size2(root.right)+1;return tmp;}

2.获取叶子节点的个数

叶子结点的特点就是度为0，即其左子树和右子树都是空。

这个方法实现在这里有两种思路：

1.遍历这个树，只要root不为空且root的左子树和右子树都为空，就说明root所在的结点是叶子结点
2.用子问题的思路来解决：总叶子结点数=左子树的叶子结点+右子树的叶子结点

    public int leafSize;public void getLeafNodeCount(TreeNode root) {if(root == null) {return;}if(root.left == null && root.right == null) {leafSize++;}getLeafNodeCount(root.left);getLeafNodeCount(root.right);}//子问题思路：这颗树的总叶子结点数=左子树的叶子结点+右子树的叶子结点public int getLeafNodeCount2(TreeNode root) {if (root == null) {return 0;}if (root.left == null && root.right == null) {return 1;}return getLeafNodeCount2(root.left)+ getLeafNodeCount2(root.right);}

3.获取第K层节点的个数

    public int getKLevelNodeCount(TreeNode root,int k){if (root==null){return 0;}if (k==1){return 1;}return getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);}

4.获取二叉树的高度

整棵树的高度=找出左子树的高度和右子树的高度的最大值 +1（树的高度或深度：树中结点的最大层次）

    // 获取二叉树的高度public int getHeight(TreeNode root){if(root==null){return 0;}int leftHeight=getHeight(root.left);int rightHeight=getHeight(root.right);return Math.max(leftHeight,rightHeight)+1;}

5. 检测值为value的元素是否存在

1.先判断根节点的值是不是我们要找的value，如果是就返回这个root

2.如果当前根节点不是我们要找的value，那就到当前根节点的左子树去找，如果左子树找不到就去右子树找。

// 检测值为value的元素是否存在private TreeNode find(TreeNode root, int val){if (root==null){return null;}if (root.val==val){System.out.println(root.val);return root;}TreeNode leftval=find(root.left,val);if(leftval!=null){return leftval;}TreeNode rightval=find(root.right,val);if (rightval!=null){return rightval;}return null;}

6.层序遍历

先入队根节点，然后出队，若当前根节点左右不为空，则把不为空的左右入队，出新的队头，以此类推。

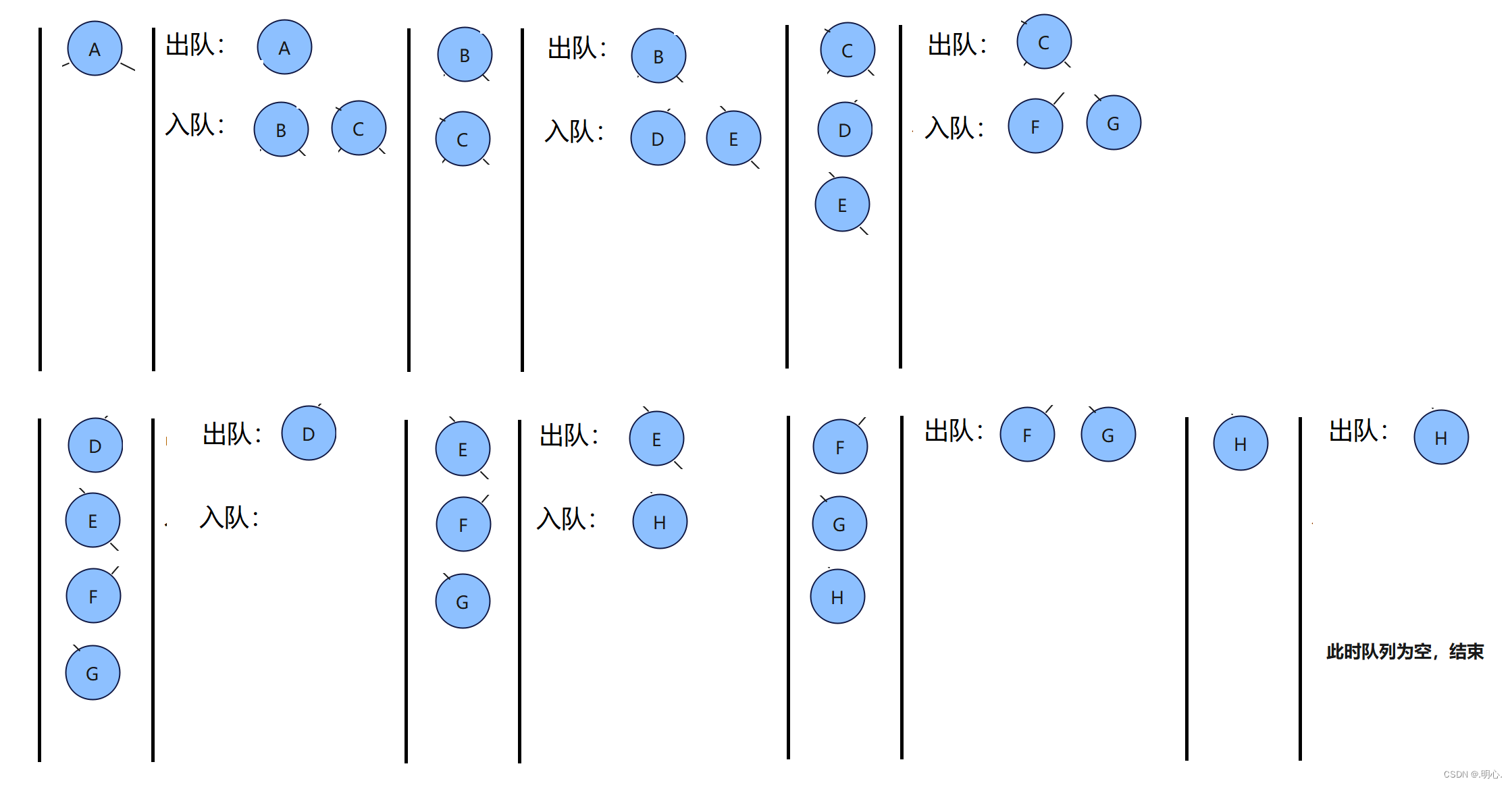
   public void levelOrder(TreeNode root) {if(root == null) {return;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode cur = queue.poll();System.out.print(cur.val+" ");if(cur.left != null) {queue.offer(cur.left);}if(cur.right != null) {queue.offer(cur.right);}}}

7.判断一棵树是不是完全二叉树

1.先把根节点放到队列当中

2.队列不为空，弹出元素，带入左右(可以为空)

3.当队列弹出元素为null则停止

4.最后一步，判断当前队列是否元素都是nul，只要出现不为nul的元素，则当前二又树不是完全二叉树

   public boolean isCompleteTree(TreeNode root) {if(root == null) return true;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode cur = queue.poll();if(cur != null) {queue.offer(cur.left);queue.offer(cur.right);}else {break;//结束之后  遍历队列剩下的所有元素 是不是都是null}}// 遍历队列剩下的所有元素 是不是都是nullwhile (!queue.isEmpty()) {TreeNode cur = queue.poll();if(cur != null) {return false;}}return true;}

查看全文

http://www.dinnco.com/news/21256.html