南山商城网站建设多少钱奶茶软文案例300字

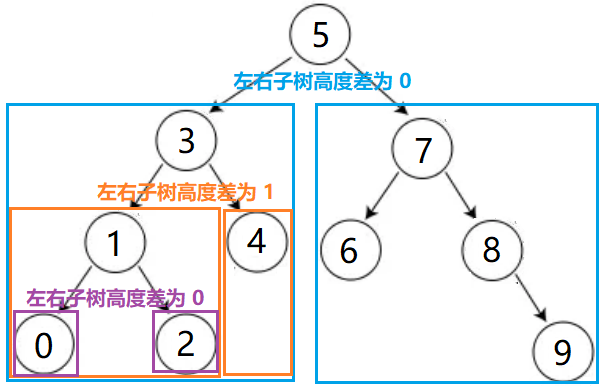
一、AVL 树的概念

在 二叉搜索树 中，当我们连续插入有序的数据时，二叉搜索树可能会呈现单枝树的情况，此时二叉搜索树的查找效率为 O(N)

俄罗斯的两位数学家 G. M. Adelson-Velsky 和 E. M. Landis 发明了 AVL 树可以解决上述问题，AVL 树保证树中的每个结点的左右子树高度差不会超过 1，从而保证 AVL 树是一颗高度平衡的二叉搜索树，从而保证 AVL 树的搜索效率为 O(log N)，AVL 树的名字就是取自于这两位科学家

一颗 AVL 树是 空树 或者满足如下条件：

• 左右子树的高度差小于等于 1 的二叉搜索树
• 左右子树均为 AVL 树

AVL 树是一颗在二叉搜索树并且满足所有结点的左右子树高度差不超过 1

二、AVL 树的实现

AVL 树有很多实现方式，这里采用三叉链和平衡因子，结点的平衡因子的值为右子树的高度减去左子树的高度，通过控制所有结点的平衡因子的绝对值小于等于 1，并且保证该树为二叉搜索树，即可实现 AVL 树

1. AVL 树的存储结构

// AVL 树的结点
template<class K, class V>
struct AVLTreeNode
{std::pair<K, V> _kv;AVLTreeNode<K, V>* _parent;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;int _bf;	// 平衡因子: 右子树的高度前去左子树的高度AVLTreeNode<K, V>(const std::pair<K, V>& kv = std::pair<K, V>(K(), V())): _kv(kv), _parent(nullptr), _left(nullptr), _right(nullptr), _bf(0){}
};// AVL 树
template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:AVLTree<K, V>(): _root(nullptr){}private:Node* _root;
};

2. AVL 树的插入

首先按照二叉搜索树的方式插入结点，保证插入结点之后还是二叉搜索树，当插入结点完成之后，该结点的祖先结点的平衡因子可能会受到影响，如果插入结点在祖先结点的左子树中，则祖先结点的 _bf --，否则该结点的 _bf ++(平衡因子的值为右子树的高度减去左子树的高度)

祖先结点的 _bf 更新后，有三种情况 _bf == 0 和 _bf == -1 || _bf == 1 以及 _bf == -2 || _bf == 2

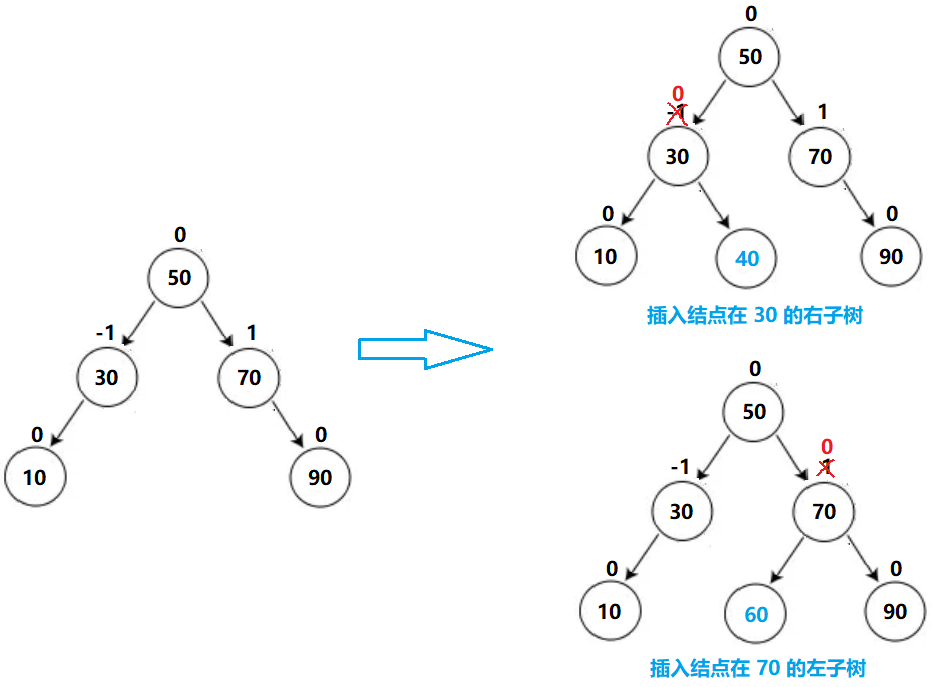
• 当 _bf == 0 时：当前更新 _bf 的结点所在的子树高度没有变化，此时不用继续更新祖先结点的 _bf

如果插入结点在祖先结点的右子树，祖先结点的平衡因子从 -1 -> 0
如果插入结点在祖先节点的左子树，祖先结点的平衡因子从 1 -> 0

无论是这两种的那种情况，对于更新后 _bf == 0 的结点的祖先结点而言，子树的高度是没有变化的

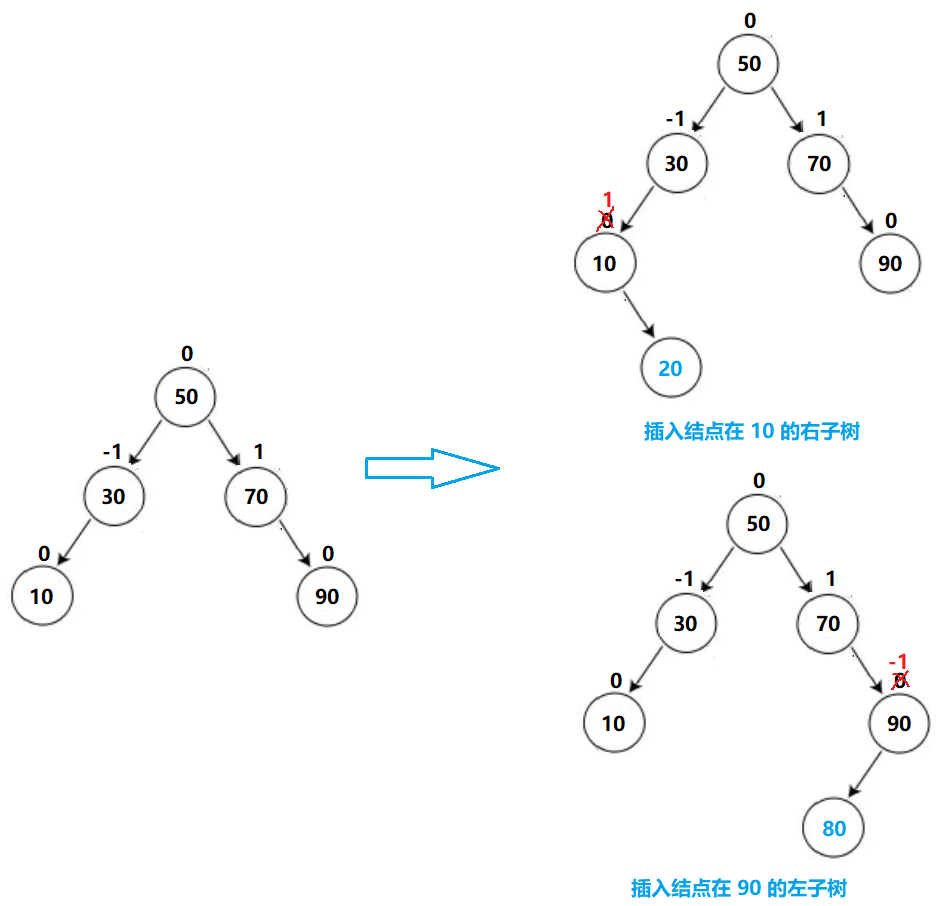
• 当 _bf == -1 || _bf == 1 时，当前更新 _bf 的结点所在的子树高度增加了，此时需要继续更新祖先结点的 _bf

如果插入结点在祖先结点的右子树，祖先结点的平衡因子从 0 -> 1
如果插入结点在祖先节点的左子树，祖先结点的平衡因子从 0 -> -1

无论是这两种的那种情况，对于更新后 _bf == -1 || _bf == 1 的结点的祖先结点而言，子树的高度都增加了 1

• 当 _bf == -2 || _bf == 2 时，当前更新 _bf 的结点左右子树高度差超过 1 了，已经不平衡了，此时需要对该结点所在的子树进行旋转，旋转之后该结点的 _bf 会变成 0，此时也不用继续更新祖先结点的 _bf 了

旋转有四种情况：右单旋、左单旋、左单旋再右单旋、右单旋再左单旋

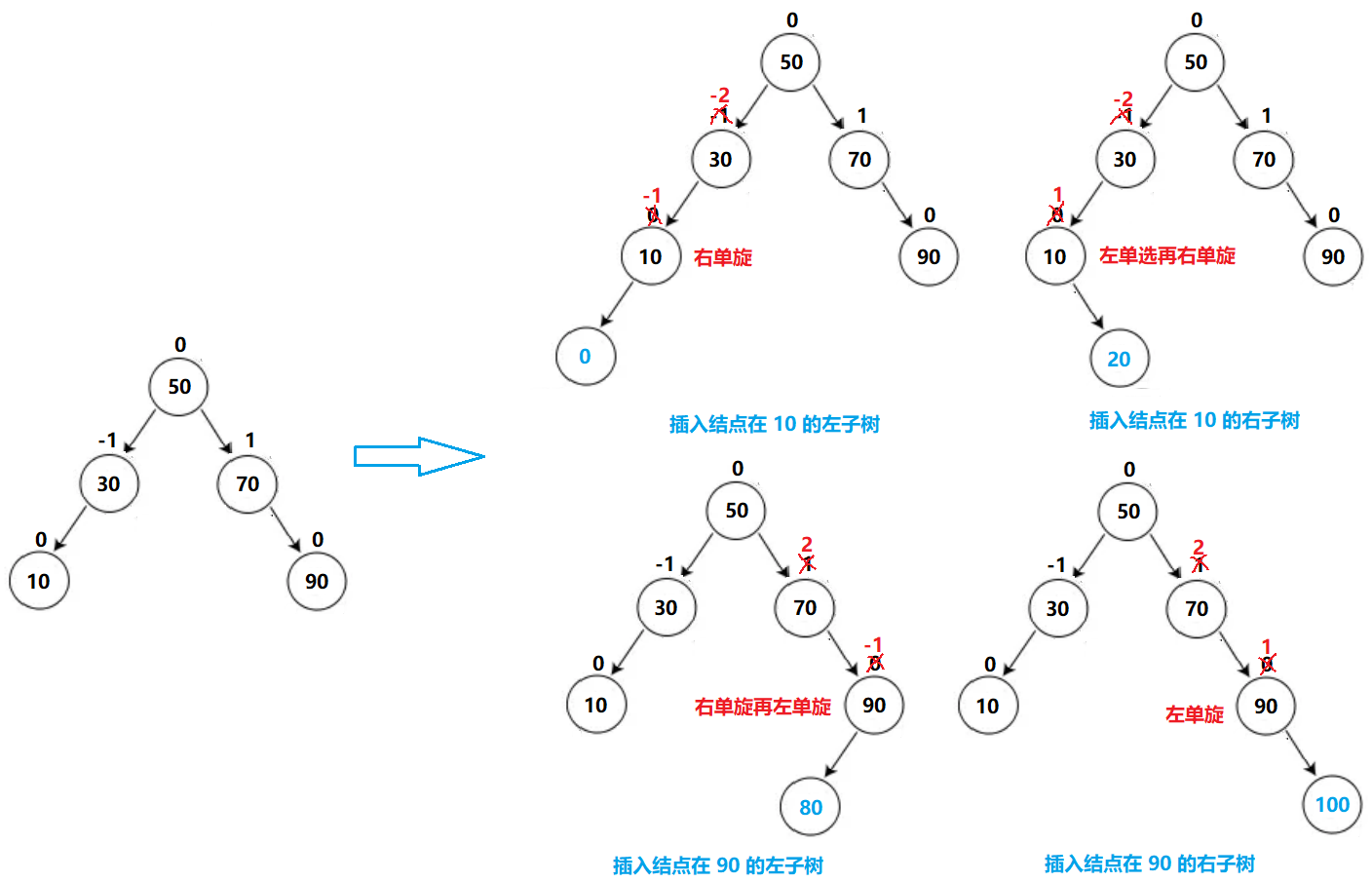
• 右单旋：插入结点在较高左子树的左侧

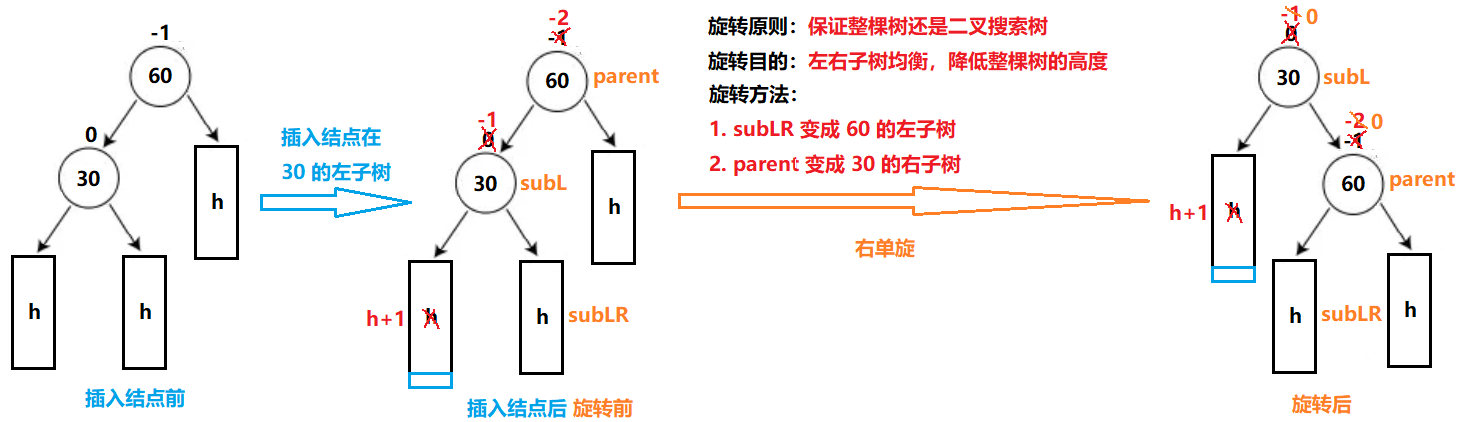
• 左单旋：插入结点在较高右子树的右侧，旋转方法类似于右单旋

• 左单旋再右单旋：插入结点在较高左子树的右侧，旋转方法类似于右单旋再左单旋

• 右单旋再左单旋：插入结点在较高右子树的左侧

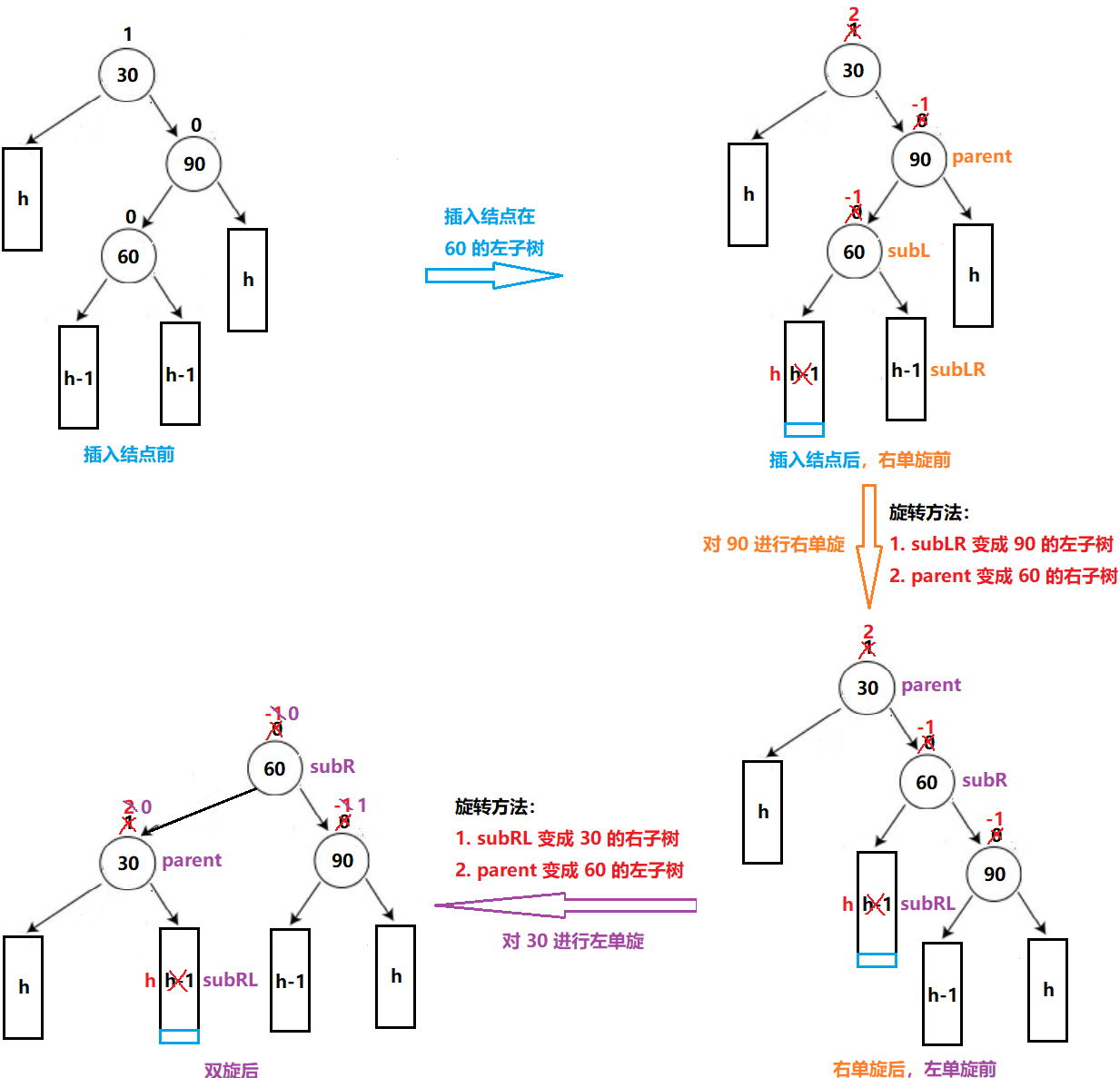
// 右单旋
void RotateR(Node* parent)
{Node* pparent = parent->_parent;Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR) subLR->_parent = parent;subL->_right = parent;parent->_parent = subL;if (pparent == nullptr) _root = subL;else{if (pparent->_kv.first > subL->_kv.first) pparent->_left = subL;else pparent->_right = subR;}subL->_parent = pparent;
}// 左单旋
void RotateL(Node* parent)
{Node* pparent = parent->_parent;Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL) subRL->_parent = parent;subR->_left = parent;parent->_parent = subR;if (pparent == nullptr) _root = subR;else{if (pparent->_kv.first > subR->_kv.first) pparent->_left = subR;else pparent->_right = subR;}subR->_parent = pparent;
}// 插入
bool Insert(const std::pair<K, V>& kv)
{// 按照二叉搜索树的方式插入结点，保证该树插入结点之后还是二叉搜索树if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else return false;}cur = new Node(kv);if (parent->_kv > kv.first) parent->_left = cur;else parent->_right = cur;cur->_parent = parent;// 更新平衡因子while (parent){// 如果插入结点在祖先结点的左子树，_bf--// 如果插入结点在祖先结点的右子树，_bf++if (parent->_left == cur) parent->_bf--;else parent->_bf++;// 当 _bf == 0 时，结点所在的子树高度没有变化，不用继续更新祖先结点的 _bf// 当 _bf == -1 || _bf == 1 时，结点所在的子树高度增加 1，需要继续更新祖先结点的 _bf，最多更新到根结点// 当 _bf == -2 || _bf == 2 时，结点所在的子树不平衡了，需要对子树进行旋转，旋转之后 _bf 变为 0，也不用继续更新祖先结点的 _bf 了// 当 _bf 为其他值时，说明出大问题了if (parent->_bf == 0) break;else if (parent->_bf == -1 || parent->_bf == 1){// 继续更新parent = parent->_parent;cur = cur->_parent;}else if (parent->_bf == -2 || parent->_bf == 2){// 旋转// parent->_bf == -2 && cur->_bf == -1 右单旋// parent->_bf ==  2 && cur->_bf ==  1 左单旋// parent->_bf == -2 && cur->_bf ==  1 左单旋再右单旋// parent->_bf ==  2 && cur->_bf == -1 右单旋再左单旋// 当 _bf 为其他值时，说明出大问题了if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);parent->_bf = 0;cur->_bf = 0;}else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);	parent->_bf = 0;cur->_bf = 0;}else if (parent->_bf == -2 && cur->_bf == 1){Node* sub = cur->_right;int bf = sub->_bf;RotateL(cur);RotateR(parent);// bf ==  0 sub 就是新增// bf == -1 sub 左边新增// bf ==  1 sub 右边新增sub->_bf = 0;if (bf == 0){parent->_bf = 0;cur->_bf = 0;}else if (bf == -1){parent->_bf = 1;cur->_bf = 0;}else if (_bf == 1){parent->_bf = 0;cur->_bf = -1;}else assert(false);}else if (parent->_bf == 2 && cur->_bf == -1){Node* sub = cur->_left;int bf = sub->_bf;RotateR(cur);RotateL(parent);// bf ==  0 sub 就是新增// bf == -1 sub 左边新增// bf ==  1 sub 右边新增sub->_bf = 0;if (bf == 0){parent->_bf = 0;cur->_bf = 0;}else if (bf == -1){parent->_bf = 0;cur->_bf = 1;}else if (bf == 1){parent->_bf = -1;cur->_bf = 0;}else assert(false);}else assert(false);break;}else assert(false);}return true;
}