---

什么是二分查找

二分查找针对的是一个有序的数据集合，查找思想有点类似分治思想。每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为 0。

我们来举个例子，假设只有 10 个订单，订单金额分别是：8，11，19，23，27，33，45，55，67，98。现在要查找金额为19的订单是否存在，利用二分思想，每次都与区间的中间数据比对大小，缩小查找区间的范围。为了更加直观，我画了一张查找过程的图。其中，low 和 high 表示待查找区间的下标，mid 表示待查找区间的中间元素下标。

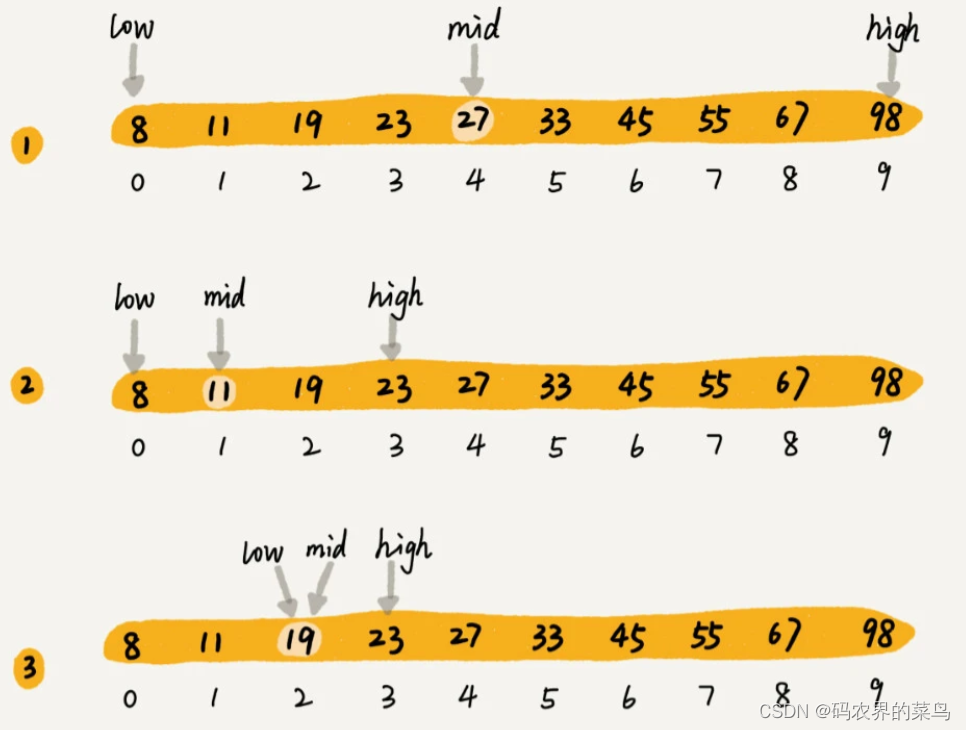
二分查找的时间复杂度

我们假设数据大小是 n，每次查找后数据都会缩小为原来的一半，也就是会除以 2。最坏情况下，直到查找区间被缩小为空，才停止。

可以看出来，这是一个等比数列。其中 n/2k=1 时，k 的值就是总共缩小的次数。而每一次缩小操作只涉及两个数据的大小比较，所以，经过了 k 次区间缩小操作，时间复杂度就是 O(k)。通过 n/2k=1，我们可以求得 k=log2n，所以时间复杂度就是 O(logn)。

O(logn) 这种对数时间复杂度是一种极其高效的时间复杂度，有的时候甚至比时间复杂度是常量级 O(1) 的算法还要高效。为什么这么说呢？

因为 logn 是一个非常“恐怖”的数量级，即便 n 非常非常大，对应的 logn 也很小。比如 n 等于 2 的 32 次方，这个数很大了吧？大约是 42 亿。也就是说，如果我们在 42 亿个数据中用二分查找一个数据，最多需要比较 32 次。

我们前面讲过，用大 O 标记法表示时间复杂度的时候，会省略掉常数、系数和低阶。对于常量级时间复杂度的算法来说，O(1) 有可能表示的是一个非常大的常量值，比如 O(1000)、O(10000)。所以，常量级时间复杂度的算法有时候可能还没有 O(logn) 的算法执行效率高。

二分查找的代码实现

简单实现：不重复有序数组查找目标值

最简单的情况就是有序数组中不存在重复元素，我们在其中用二分查找值等于给定值的数据。我用 Java 代码实现了一个最简单的二分查找算法。

    public static int bSearch(int[] arr, int startIndex, int endIndex, int target) {// 递归推出条件if (startIndex > endIndex) {return -1;}// 取折中索引int mid = (startIndex + endIndex) / 2;// 折中值比较if (arr[mid] == target) {return mid;}if (arr[mid] > target) {return bSearch(arr, startIndex, mid - 1, target);}return bSearch(arr, mid + 1, endIndex, target);}

变体实现：查找第一个值等于给定值的元素

比如下面这样一个有序数组，其中，a[5]，a[6]，a[7]的值都等于 8，是重复的数据。我们希望查找第一个等于 8 的数据，也就是下标是 5 的元素。

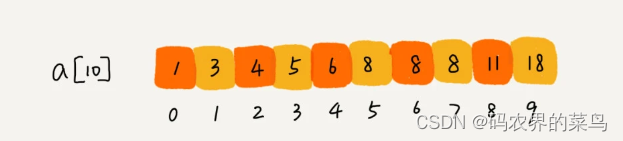
    public static int bSearchFirst(int[] arr, int startIndex, int endIndex, int target) {// 递归推出条件if (startIndex > endIndex) {return -1;}// 取折中索引int mid = (startIndex + endIndex) / 2;// 折中值比较if (arr[mid] == target) {if (mid - 1 >= startIndex && arr[mid - 1] == target) {return bSearchFirst(arr, startIndex, mid - 1, target);}return mid;}if (arr[mid] > target) {return bSearchFirst(arr, startIndex, mid - 1, target);}return bSearchFirst(arr, mid + 1, endIndex, target);}

变体实现：查找最后一个值等于给定值的元素

还是上面那个数组，我们的目标如果是查找最后一个等于8的，也就是下表为7的元素。

    public static int bSearchLast(int[] arr, int startIndex, int endIndex, int target) {// 递归推出条件if (startIndex > endIndex) {return -1;}// 取折中索引int mid = (startIndex + endIndex) / 2;// 折中值比较if (arr[mid] == target) {if (mid + 1 <= endIndex && arr[mid + 1] == target) {return bSearchLast(arr, mid + 1, endIndex, target);}return mid;}if (arr[mid] > target) {return bSearchLast(arr, startIndex, mid - 1, target);}return bSearchLast(arr, mid + 1, endIndex, target);}

变体实现：查找最后一个小于给定值的元素

还是最上面的那个数组，我们要查找最后一个小于等于8的元素，就是下标为4的元素。

    public static int bSearchLastSmaller(int[] arr, int startIndex, int endIndex, int target) {// 递归推出条件if (startIndex > endIndex) {return -1;}// 取折中索引int mid = (startIndex + endIndex) / 2;// 折中值比较if (arr[mid] < target) {if (mid == endIndex || arr[mid + 1] >= target) {return mid;}return bSearchLastSmaller(arr, mid + 1, endIndex, target);}return bSearchLastSmaller(arr, startIndex, mid - 1, target);}

变体实现：查找第一个大于给定值的元素

还是最上面的那个数组，我们要查找最后一个大于等于8的元素，就是下标为8的元素。

   public static int bSearchFirstBigger(int[] arr, int startIndex, int endIndex, int target) {// 递归推出条件if (startIndex > endIndex) {return -1;}// 取折中索引int mid = (startIndex + endIndex) / 2;// 折中值比较if (arr[mid] > target) {if (mid - 1 <= 0 || arr[mid - 1] <= target) {return mid;}return bSearchFirstBigger(arr, startIndex, mid - 1, target);}return bSearchFirstBigger(arr, mid + 1, endIndex, target);}

二分查找的局限性

• 首先，二分查找依赖的是顺序表结构，简单点说就是数组
    二分查找能否依赖其他数据结构呢？比如链表。答案是不可以的，主要原因是二分查找算法需要按照下标随机访问元素。我们在数组和链表那两节讲过，数组按照下标随机访问数据的时间复杂度是 O(1)，而链表随机访问的时间复杂度是 O(n)。所以，如果数据使用链表存储，二分查找的时间复杂就会变得很高。
    二分查找只能用在数据是通过顺序表来存储的数据结构上。如果你的数据是通过其他数据结构存储的，则无法应用二分查找。

• 其次，二分查找针对的是有序数据
    二分查找对这一点的要求比较苛刻，数据必须是有序的。如果数据没有序，我们需要先排序。前面章节里我们讲到，排序的时间复杂度最低是 O(nlogn)。所以，如果我们针对的是一组静态的数据，没有频繁地插入、删除，我们可以进行一次排序，多次二分查找。这样排序的成本可被均摊，二分查找的边际成本就会比较低。
    但是，如果我们的数据集合有频繁的插入和删除操作，要想用二分查找，要么每次插入、删除操作之后保证数据仍然有序，要么在每次二分查找之前都先进行排序。针对这种动态数据集合，无论哪种方法，维护有序的成本都是很高的。
    所以，二分查找只能用在插入、删除操作不频繁，一次排序多次查找的场景中。针对动态变化的数据集合，二分查找将不再适用。

• 再次，数据量太小不适合二分查找
    如果要处理的数据量很小，完全没有必要用二分查找，顺序遍历就足够了。比如我们在一个大小为 10 的数组中查找一个元素，不管用二分查找还是顺序遍历，查找速度都差不多。只有数据量比较大的时候，二分查找的优势才会比较明显。
    不过，这里有一个例外。如果数据之间的比较操作非常耗时，不管数据量大小，我都推荐使用二分查找。比如，数组中存储的都是长度超过 300 的字符串，如此长的两个字符串之间比对大小，就会非常耗时。我们需要尽可能地减少比较次数，而比较次数的减少会大大提高性能，这个时候二分查找就比顺序遍历更有优势。

• 最后，数据量太大也不适合二分查找
    二分查找的底层需要依赖数组这种数据结构，而数组为了支持随机访问的特性，要求内存空间连续，对内存的要求比较苛刻。比如，我们有 1GB 大小的数据，如果希望用数组来存储，那就需要 1GB 的连续内存空间。
    注意这里的“连续”二字，也就是说，即便有 2GB 的内存空间剩余，但是如果这剩余的 2GB 内存空间都是零散的，没有连续的 1GB 大小的内存空间，那照样无法申请一个 1GB 大小的数组。而我们的二分查找是作用在数组这种数据结构之上的，所以太大的数据用数组存储就比较吃力了，也就不能用二分查找了。