wordpress语音朗读南昌seo搜索优化
物理学与AI看似神秘而又简洁的纠缠
随着今年诺贝尔物理学奖(这篇还没来得及发,化学奖也...)的颁布,不管是国内某圈还是国外某管,无论是学术界又或产业界,充斥着震惊又或是“物理学不存在了”之类的调侃,甚至形成了两极分化的极端认知。
当然想借着这股热乎劲儿,再跟大伙分享下我对这个事儿的一些看法以及结合近期思考对于未来AI与物理学之间的那些看似神秘却又简洁的纠缠...
简单说明一下:本篇笔记的灵感来自于之前阅读过的多篇AI与物理学交叉学科的相关论文,不少体会也来自于《中国物理学会期刊》、王庆法老师“清熙”公号文章以及忙于各自内卷未曾谋面的知(基)己(友) · 跨国人工智能从业者 宋斐 的观点~
以史为鉴,当下物理学的研究范式虽然并不完全依赖于庞杂的数据,AI的研究方法亦并非完全遵循特定的物理学规律,但人工神经网络(HNN)和统计物理的关系在直觉与众多跨学科研究实践上是至少是非常紧密的,因此不管是对AI的研究也好还是对于物理的探索发现,一旦洞悉到HNN模型与物理学基因的相互借鉴与联系,我想就会比较容易相互借鉴、理解甚至改造它们,以至发明新的AI模型或洞悉新的物理现象。
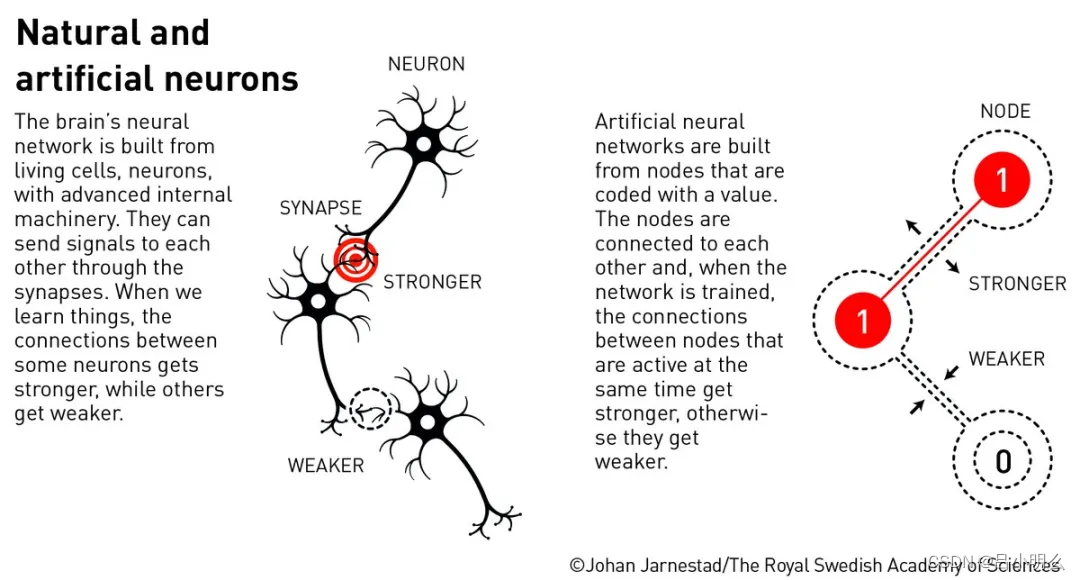
包括最近理论领域活跃的自由能理论、超图框架、重整化群..
AI与统计物理学跨学科研究下的扩散模型、流模型、伊辛模型、变分自编码器以及KAN网络..
以及两位诺奖得主Hopfield老爷子的以自旋玻璃理论为依据的Hopfield网络和Hinton老爷子的玻尔兹曼机..
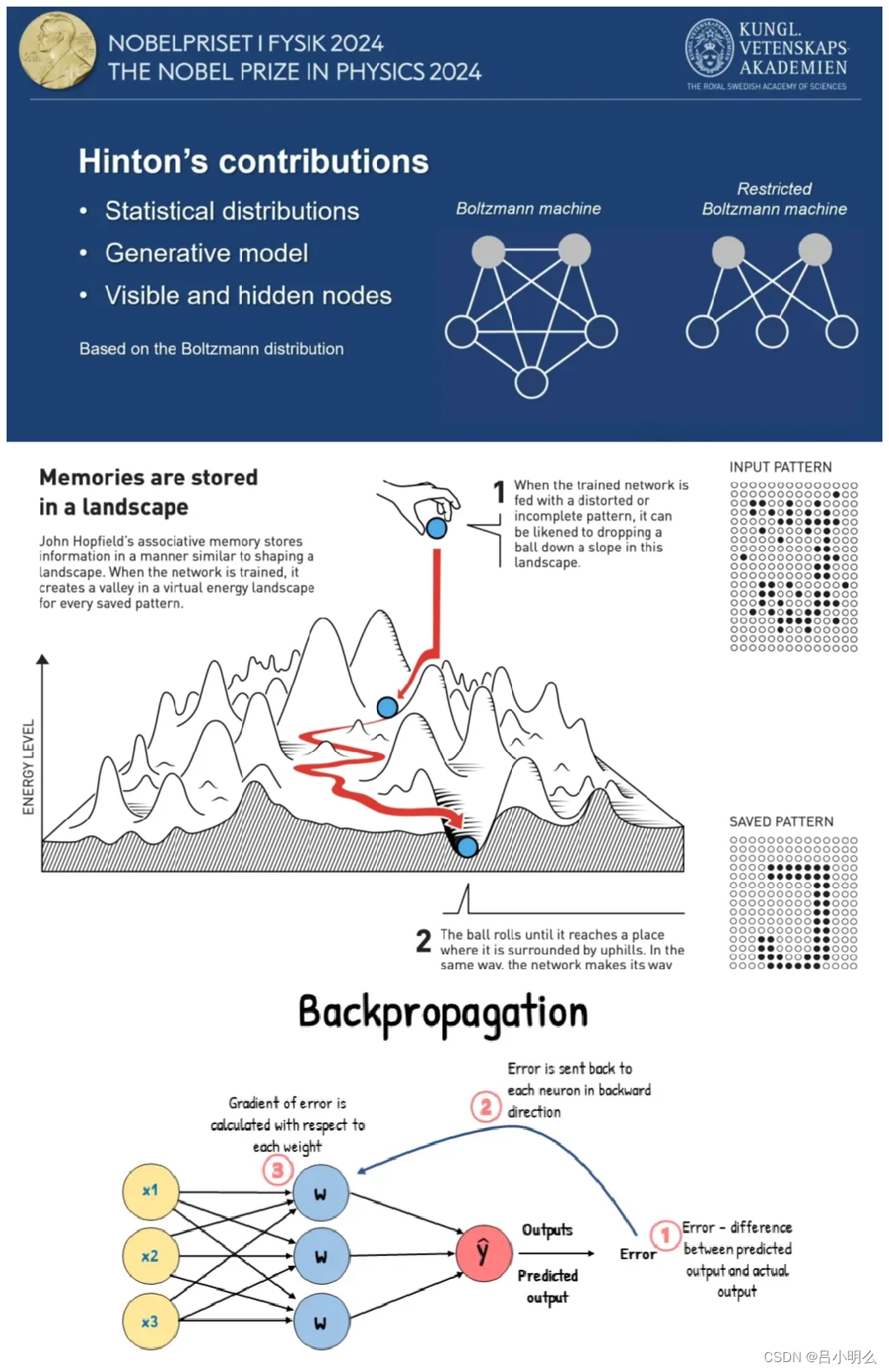
这里需要指出的是,上述两个学科的联系是可对比借鉴但不必局限的,虽说直觉上两者联系似乎很紧密,但毕竟对于当前通用智能或认知下的复杂联合概率分布与物理世界各领域下的统计物理概率分布在变换形式与机制上还未形成统一和充分的理论论证:
「也许这一研究方向将是未来建立连接物理学与认知科学的真正的桥梁」
且其关键核心内涵取决于底层更加抽象而多样化的数学变换形式与计算基础:
「如“归一化因子”对应下的贝叶斯推断中的“边际似然”与统计物理下的“配分函数或自由能计算”两者间的类比与借鉴甚至可能存在的联系;甚至更多诸如NN模型下的“对数似然函数”、“目标函数”、“隐变量”、“自回归采样”与统计物理下的“能量函数”、“力”、“微观构型作用变量”、“分子动力学模拟”的一一类比对应或可能的潜在联系」
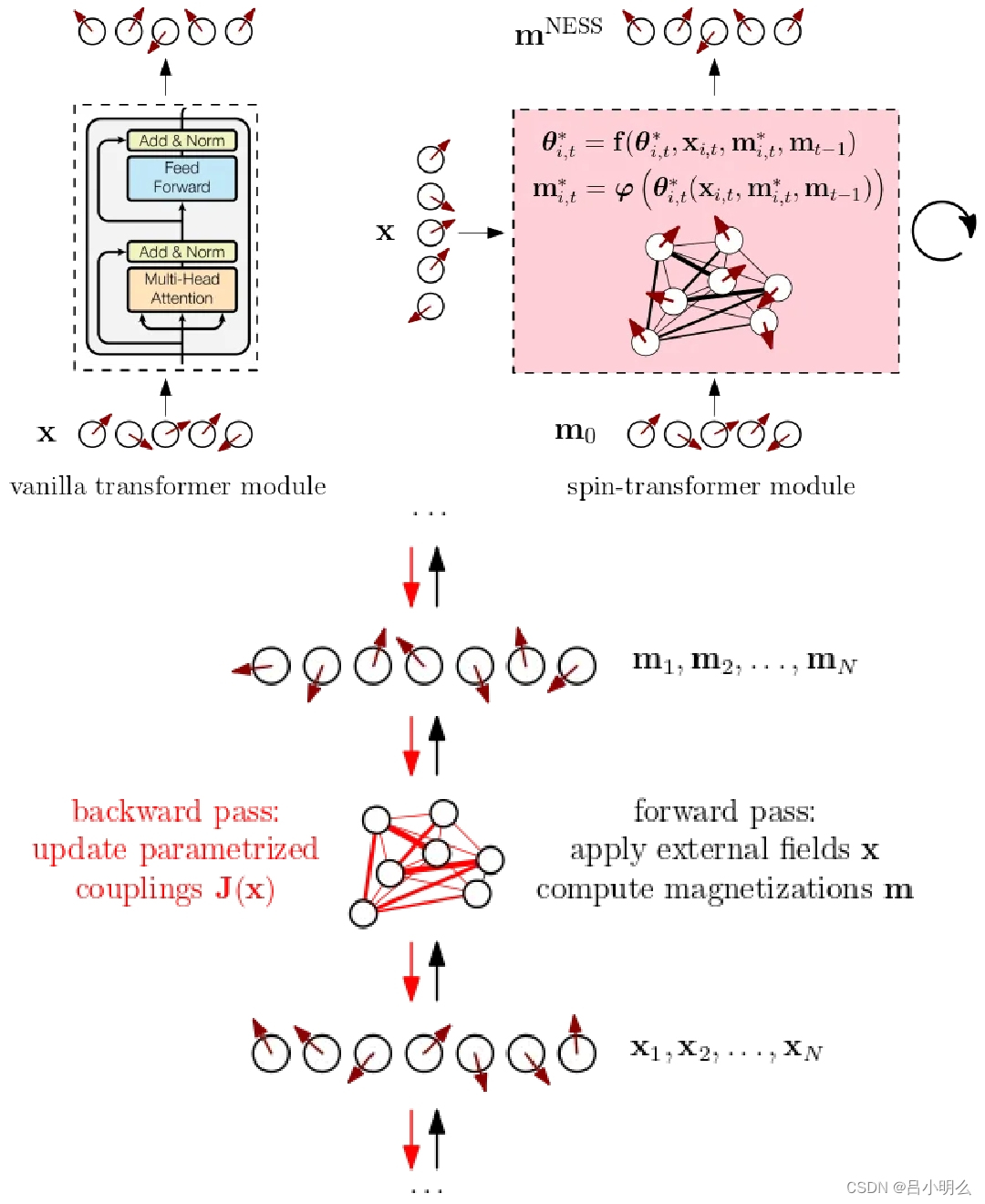
ps:至少两者间所面临在计算复杂度上的挑战是有一定共性的,哈哈;)
不过,得益于近些年信息论下的计算机科学以及人工神经网络的快速发展,在信息处理与复杂计算上我们也掌握了诸多非常强大的数学工具与思想,如相对熵即我们所熟知的Kullback—Leibler散度,以平滑的计算度量及后续渐进式的拟合两种不同数量级下概率分布下的相似性,并尝试将系列方法反哺到统计物理学的应用与实践中去,如与变分自由能计算的对齐与互补,甚至绕过基于物理原理难以计算的分子动力学模拟方法,采用扩散思想直接基于自然界已有数据采样并生成新的微观物质结构...
同时,看到很多研究尝试将连接主义下的人工神经网络的黑盒机制用某种统计物理学中所体现的微观变量概率分布现象来去作为理论基础或理论解释,从严谨性来说我觉得应该持保留意见和审视态度,但“借鉴”、“尝试”和“改造”是非常有意义的,如自由能、伊辛自旋、自旋玻璃、扩散模型中的物理扩散思想借鉴、甚至是KAN中通过B样条曲线的某种符号化形式上的模型结构嵌入。
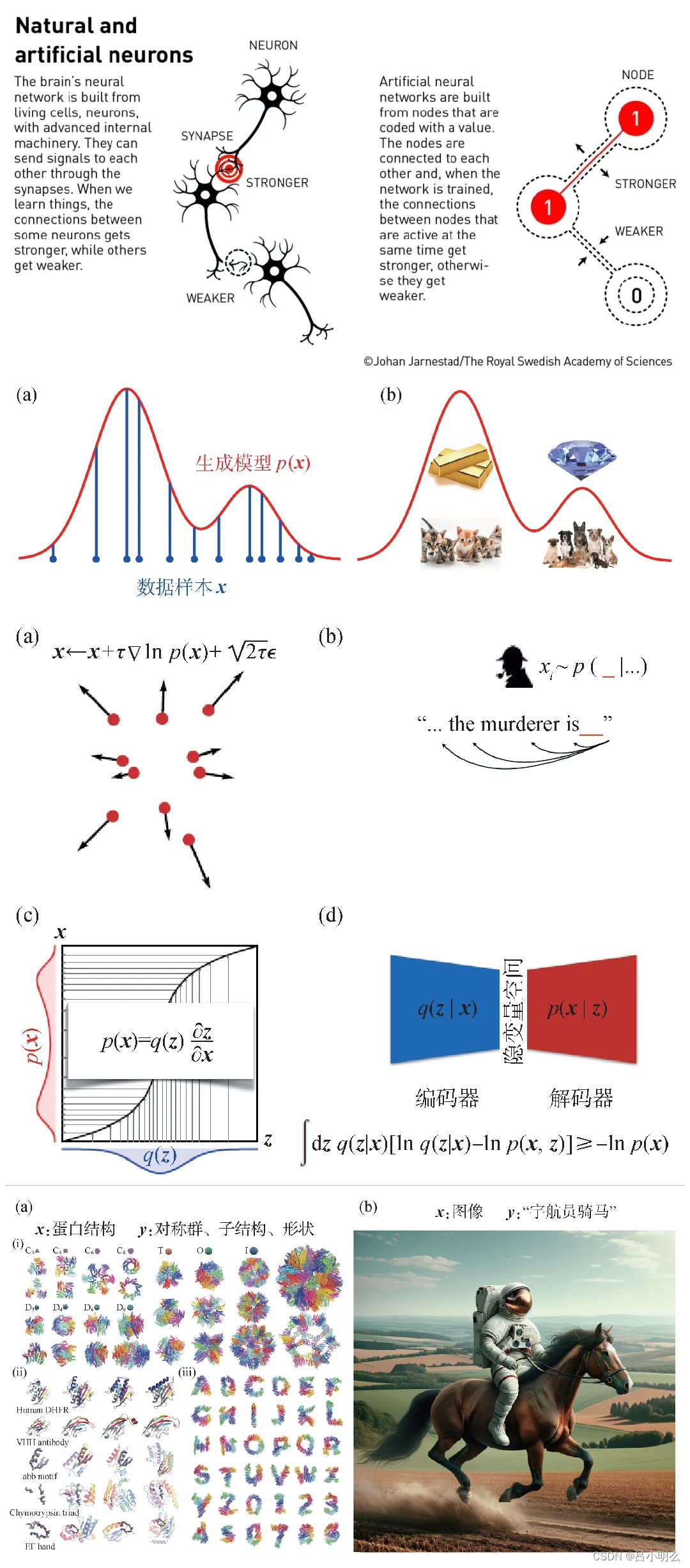
反之,上面所列举的跨学科间对应关系也暗示了人工智能中涉及的不少挑战或问题都具有和统计物理问题相似的计算难度,如计算高维概率分布函数的归一化因子涉及到理论计算科学中所谓“#P难”的一类计数问题,一般被认为不存在快速(多项式时间复杂度)的求解算法。不过,相信未来在更具跨学科创新精神的研究者们通过对纯数理空间、数学变换与数值计算的持续探索、求解下,诸如采用上述相对熵对于目标函数的巧妙利用以绕过相关挑战,为高维变量的概率建模和变分计算打开了新的可能。

我想,也许这就是这次诺贝尔物理学与化学奖颁布下对于未来科学范式S2AI&AI4S的启示吧。
希望上述内容能够帮助到大伙,或解惑或进一步激发大家对物理学与AI的兴趣并保持对当下与未来物理学与AI创新研究的多一分理解和善待,同时,鉴于受限当前宏观或微观物理学的观测瓶颈以及人们仍对认知智能的某种未知局限,也希望各界保持更多的耐心和期待!
作者:吕明
