电子商务专业就业方向及就业前景企业网站seo排名优化

平均数用更少的数字，概括一组数字。属于概述统计量、集中趋势测度、位置测度。中位数是第二常见的概述统计量。许多情况下比均值更合适。算术平均数是3中毕达哥拉斯平均数之一，另外两种毕达哥拉斯平均数是几何平均数和调和平均数。

算术平均

$$AM=\frac{1}{n}\sum _{i=1}^n{x}_i$$

几何平均

$$GM=(\prod _i^n{x}_i{)}^{\frac{1}{n}}$$

可以通过面积/体积运算来理解几何平均：两个实数a,b分别对应长方形的边和宽，则实数a,b的几何平均等于这样一个正方形的边长，这个正方形的面积与a、b组成的长方形的面积相等。

更多维度情况下类似。

调和平均

$$HM=\frac{n}{{\sum }_{i=1}^n\frac{1}{x_i}}$$

两点间包含 n 段长度相同的路程，每段路程采用不同的速度$x_i$完成，完成所有路程的平均速度就是x_i的调和平均。

平方平均数

$$QM=\sqrt{\frac{1}{n}\sum _{i=1}^n{x}_i^2}$$

平均数之间的关系

$$HM\le GM\le AM\le QM$$

关系的几何证明：

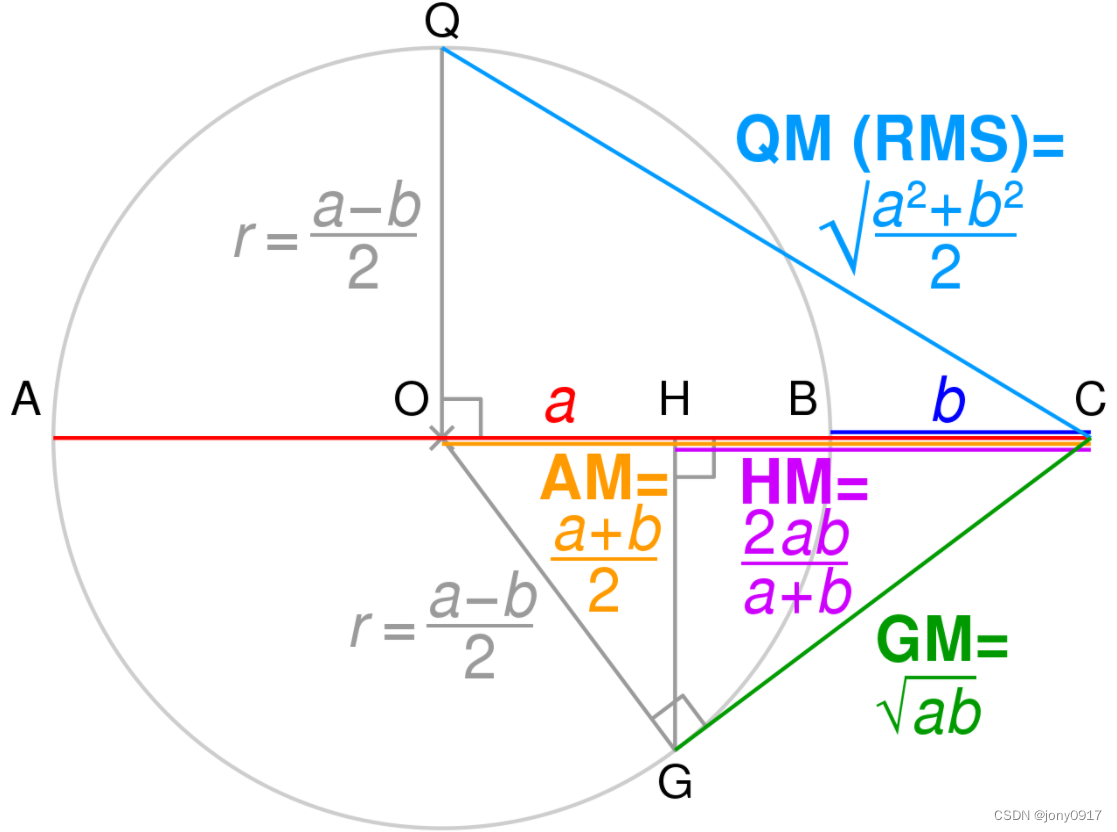
排名算法

排名问题形式简单，也就是将一组对象根据其重要性加以排序，但其解答往往不是那么简单的，充满了悖论和谜题。目前看来排名问题吸引了越来越多的人的研究兴趣，原因可能包括信息量的指数增长，数据收集能力的增强。排名的对象五花八门，比如网页、视频、直播、新闻、股票、球队等等。

排名聚合的目的是通过某种算法将多个排名结果加以融合，产出最终的单一的更好的排名结果。平均法是比较常见的排名聚合的方法，下面讨论采用不同的均值算法对排名结果的影响。

• 调和平均:
  • $$HM=\frac{2}{1/x+1/y},\frac{\partial HM}{\partial x}=2(\frac{1}{1+x/y}{)}^2,\frac{\partial HM}{\partial y}=2(\frac{1}{1+y/x}{)}^2$$
  • 自变量x, y中较小者的导数较大，平均值结果受到较小值的影响较大
• 几何平均数
  • $$GM=\sqrt{xy},\frac{\partial GM}{\partial x}=\frac{1}{2}\sqrt{\frac{y}{x}},\frac{\partial GM}{\partial y}=\frac{1}{2}\sqrt{\frac{x}{y}}$$
  • 自变量x, y中较小者的导数较大，且在接近零的时候导数趋向无穷大，因此几何平均数在零附近的极小值极为敏感。
• 算术平均数
  • $$AM=\frac{x+y}{2},\frac{\partial AM}{\partial x}=0.5,\frac{\partial AM}{\partial y}=0.5$$
  • 自变量x, y导数恒定不变，不偏袒较小值和较大值
• 平方平均数
  • $$QM=\sqrt{\frac{x^2+y^2}{2}},\frac{\partial QM}{\partial x}=\sqrt{\frac{2}{1+(y/x{)}^2}},\frac{\partial QM}{\partial y}=\sqrt{\frac{2}{1+(x/y{)}^2}}$$
  • 自变量x, y中较大者的导数较大，平均值受较大值的影响较大

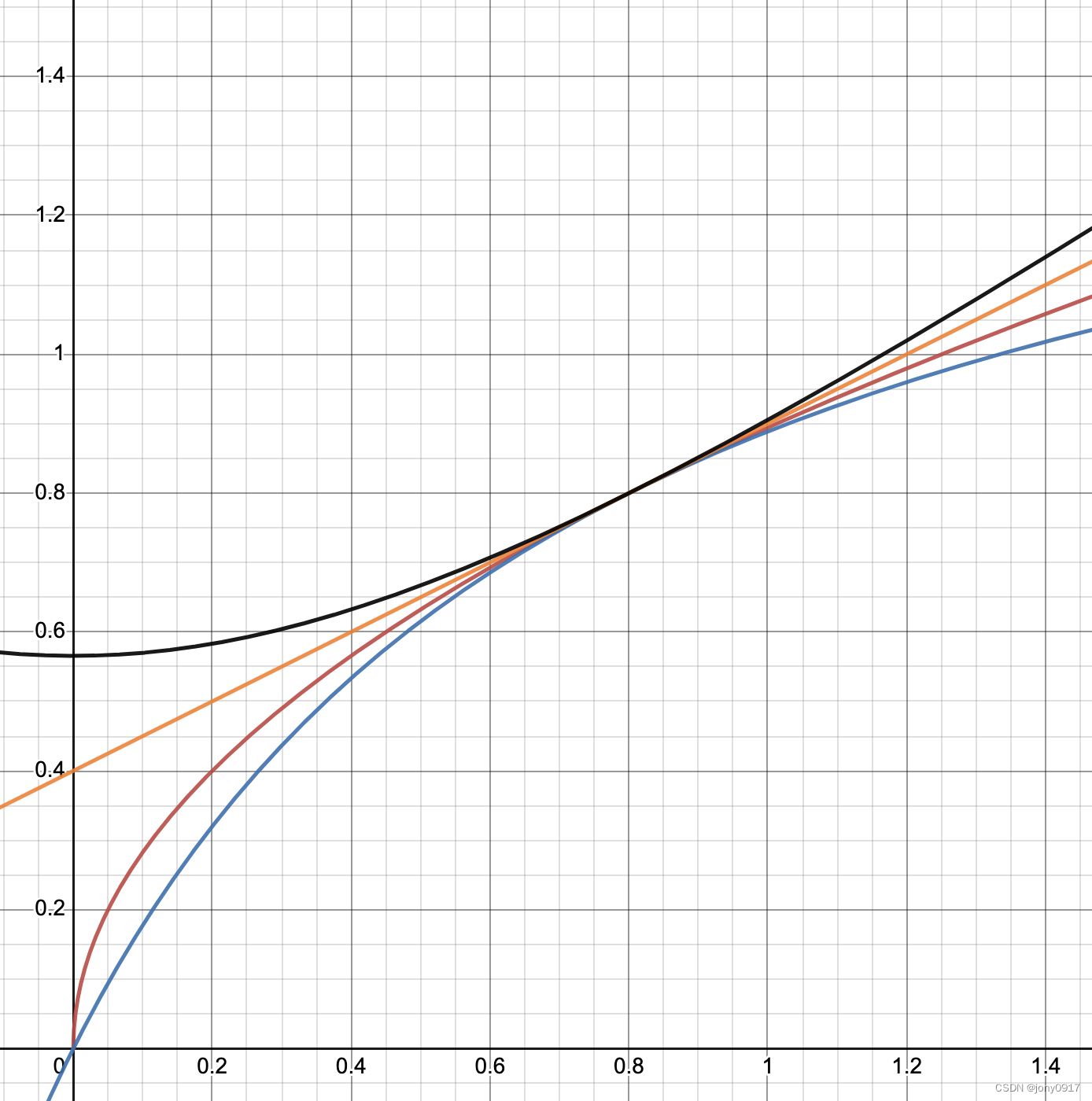
例子：考虑$x,y\in (0,1)$, 且固定 y = 0.8，观测均值随x的变化趋势（黑色：QM，橘色：AM，红色：GM，蓝色：HM）

• $x\in (0,0.2)$ ，随着x的增大，平方平均数几乎持平，算术平均数已0.5的恒定速度增长，几何平均数增长速度最大，调和平均数增长速度紧次于几何平均数；在 x 远小于 y 的区域，平方平均数几乎不受x变化的影响，算术平均值以恒定的0.5的比例受到x变化的影响，几何平均数以远大于0.5的比例受x变化的影响，调和平均数的影响比例介于几何平均数和算术平均数之间。
• $x\in (0.2,0.8)$，随着 x 的继续增大，对平方平均数的影响逐渐递增，算术平均数的变化率依旧不变，几何平均数从左侧接近0.5，调和平均数与几何平均数类似
• $x\in (0.8,1.0)$，随着 x 的继续增大，对平方平均数的影响继续递增，超过所有其他平均数，算术平均的变化率依然保持恒定，几何平均数变化率下降到0.5以下，但高于调和平均数。

因此在对具有多个排序属性值的对象继续排序

• 算术平均值对多属性值的量纲不敏感，选取的对象可能是个别属性特长的，也可以是综合能力（不存在短板属性）都不错的
• 几何平均和调和平均值对较小属性值敏感，如果对象存在短板属性，则整体排名不会太高，因此选出来的对象倾向于综合能力不错，不存在明显短板的内容
• 平方平均值对较大值比较敏感，因此选出的内容倾向于某些熟悉特长的对象，存不存在短板影响不是很大

上文的分析对设计排名算法的启发是：

• 多个属性缺一不可，不能有短板的情况下，适宜几何平均数和调和调和平均数：比如信息检索中的指标f1，是模型查准率precision和查全率recall的调和平均数，原因是一个有使用价值的模型，不能存在明显的偏科，大部分情况下precision = 0.9, recal = 0.1的模型，不如precisio = 0.6,recall = 0.6的模型，查准率查全率太小的模不具有实用价值。几何平均和调和平均排名中，值域小的属性对结果的影响较大，值域大的熟悉对结果影响较小，一点层度上有些反直觉
• 容许多个属性出现某些短板，适宜算术平均值：比如一般的考试成绩汇总，采用的是加法求和，其实等价于算术平均，算术平均允许某些科目有短板，只要考生有另外一些特长科目，整体排名也会不错，又或则考试没有明显的特长，但也没有明显的短板，排名也会不错。
• 平方平均数鼓励特长，惩罚中庸，与几何平均和调和平均相对的另一个极端。

几个属性值同分布的情况下，几类排序算法是等价的。但拉齐分布的隐射过程，可能会导致失去了原始值的信息。