辽宁省建设机械协会官方网站搜索图片识别
目录
一,插入排序
插入排序C语言实现(升序)
1,将新元素插入到有序序列
2,循环的开始与终止
二,希尔排序
希尔排序C语言实现(升序)
1,单趟:
2,循环及终止:
一,插入排序
插入排序的工作方式像许多人排序一手扑克牌。开始时,我们的左手为空并且桌子上的牌面向下。然后,我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置,我们从右到左将它与已在手中的每张牌进行比较。拿在左手上的牌总是排序好的,原来这些牌是桌子上牌堆中顶部的牌。
插入排序是指在待排序的元素中,假设前面n-1(其中n>=2)个数已经是排好顺序的,现将第n个数插到前面已经排好的序列中,然后找到合适自己的位置,使得插入第n个数的这个序列也是排好顺序的。按照此法对所有元素进行插入,直到整个序列排为有序的过程,称为插入排序。
以将数组nums[9]={9,8,7,6,5,4,3,2,1}排为升序为例

现在有九张扑克,我们摸到第一张9之后,我们认为一张牌就是有序的;然后我们摸到第二张牌8,为了将手中的牌排为升序(小的牌放左边,大的牌放右边),我们首先要比较摸到的牌和原先手里的牌的大小关系,发现8比9小,要放在9的左边。以此类推,每次都将摸到的牌与手里的牌进行比较,找到新牌合适的位置进行插入。
注意:因为从摸到第一张牌开始手里的牌就是有序的,所以手里的牌是有序的
插入排序C语言实现(升序)
可以发现,将新的元素插入到已经有序的序列中是一个循环过程,直到不再有要插入的元素
1,将新元素插入到有序序列
首先我们要清楚,新元素就是再有序序列之后的第一个元素,这个新元素和有序序列都是数组的元素。之所以要强调有序序列和新元素这两个概念,是为了更加直观的感受插入的过程
//代码不完整,仅仅示例
void InsetSort(int* nums, int numsSize)
{int end;int temp = nums[end+1];while (end >= 0 && nums[end] > temp){nums[end + 1] = nums[end];end--;}nums[end + 1] = temp;
}注释:
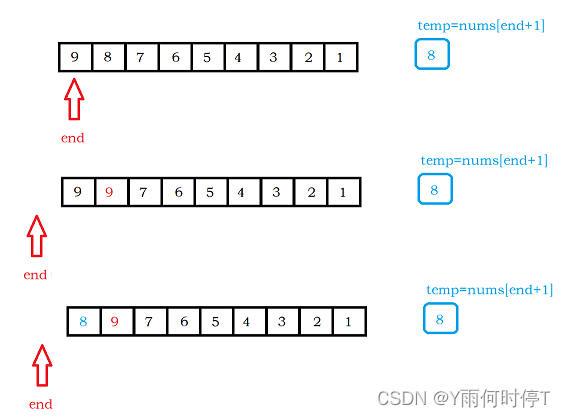
下标end表示有序序列的最后一个元素的下标,表示数组中下标0到end是有序的,temp储存的是新元素的值,也就是nums[end+1]。
为了将新元素插入到合适的位置,数组中下标为0到end+1的部分要进行数据的挪动,通过end遍历0到end这一部分元素,
如果end所指向的元素的值大于temp,则将其向后挪动一位,即nums[end + 1] = nums[end];如果end所指向的元素的值小于temp,则end+1的位置即为temp的位置
2,循环的开始与终止
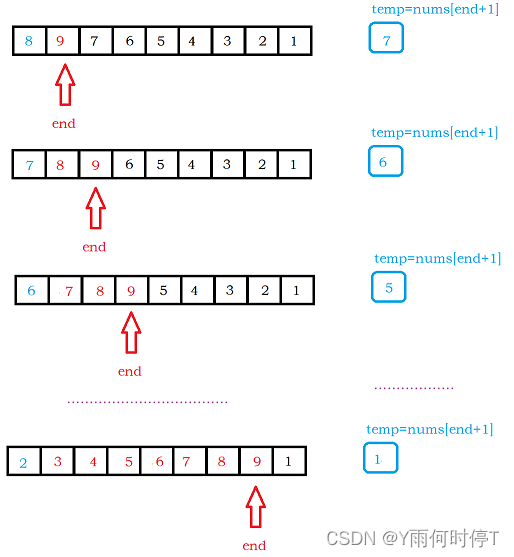
当end为0时,通过将新元素插入到有序序列中,使得数组下标0到1的部分变为有序,那么为了使整个数组有序,end需要从0到numsSize-1,逐步进行插入新元素,循环结束则排序完成
void InsetSort(int* nums, int numsSize)
{for (int i = 0; i < numsSize - 1; i++){int end = i;int temp = nums[i + 1];while (end >= 0 && nums[end] > temp){nums[end + 1] = nums[end];end--;}nums[end + 1] = temp;}
}二,希尔排序
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”,是直接插入排序算法的一种更高效的改进版本。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至 1 时,整个文件恰被分成一组,算法便终止。
注:希尔排序之所以高效,是因为插入排序的特性(一个数组越是接近有序,插入排序就越高效(若为有序数组,时间复杂度则为O(N))。希尔排序则依据此特性,先对数组进行数次预排序,使数组接近有序,最后再使用插入排序,完成升序
以将数组nums[9]={9,8,7,6,5,4,3,2,1}排为升序为例
初始状态:gap=9/2=4,数组分为4组,分别对每组进行插入排序
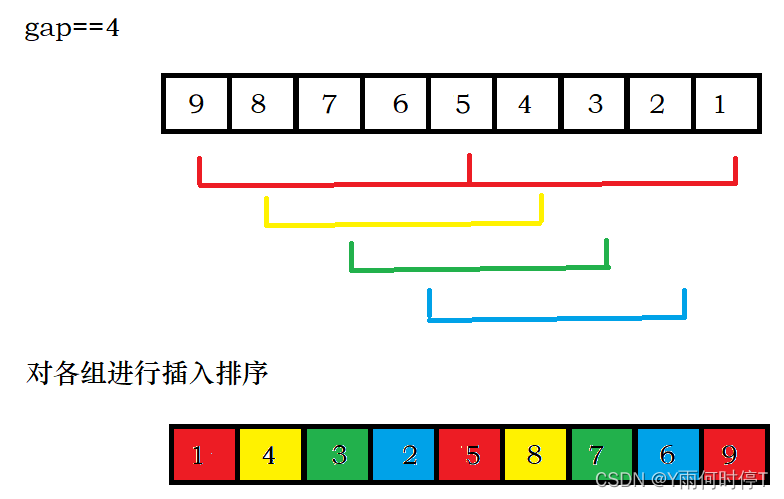
迭代状态:gap=4/2=2,数组分为2组,分别对每组进行插入排序
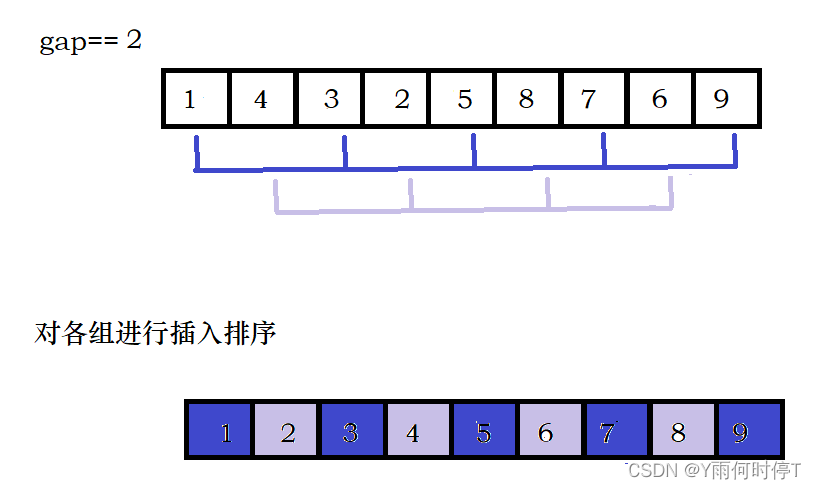
终止状态:gap=2/2=1,数组分为1组,分别对每组进行插入排序,即对整个数组进行插入排序

希尔排序C语言实现(升序)
1,单趟:
每个分组(根据增量gap划分)之间进行插入排序;
2,循环及终止:
增量是变化的,当变为1时完成排序并结束
void ShellSort(int* nums, int numsSize)
{for (int gap = numsSize / 2; gap >= 1; gap /= 2){for (int i = 0; i < numsSize - gap; i++){int end = i;int temp = nums[end + gap];while (end >= 0 && nums[end] > temp){nums[end + gap] = nums[end];end -= gap;}nums[end + gap] = temp;}}
}