做海报有哪些网站各大网站收录查询
我们继续来随机看五道AMC8的真题和解析,根据实践经验,对于想了解或者加AMC8美国数学竞赛的考生来说,吃透AMC8历年真题是备考更加科学、有效的方法之一。
最近有家长朋友问我,现在有哪些类似于奥数的比赛可以参加?我的建议可以关注下AMC8的竞赛,类似于国内的奥数,但是其难度要比国内的奥数低一些,而且比赛门槛更低,考试也更方便。比赛的题目尤其是应用题比较有趣,题目是中英文对照的,不用担心孩子英语的问题。
另一个方面,即使不参加AMC8竞赛,吃透了历年真题600道和背后的知识体系,那么小学和初中数学一定会学得非常轻松、游刃有余。(我个人建议孩子有余力的情况下还是参加,以赛促学是一种很不错的做法,能够激发孩子的好胜心和学习热情,也是孩子宝贵的经历、体验。)

为帮助孩子们更高效地备考,我整理了2000-2004年的全部AMC8真题(完整版共600道,且修正了原试卷中的少量bug),并且独家制作了多种在线练习,利用碎片化时间,一年足以通过自学在2025年AMC8竞赛中取得好成绩。详情见文末。
好消息,2000-2024年官方发布的高清版AMC8的真题和答案免费赠送,在线练习集免费体验,如有需要的朋友们欢迎联系。
2000-2024年AMC8真题和解析:2019年第7题

这道题的考点是算术、代数,列一元一次方程解应用题。
我们假设Shauna最后2场考试的分数分别为x和y,那么可以得到方程:(76+94+87+x+y)/5=81,即(257+x+y)/5=81,即257+x+y=405,x+y=148。即Shauna最后2场考试的总分为148分不变,要使得其中一场考试分数最低,则需要令另外一场考试的分数最高,最高是100 分,那么这场考试最低是48。答案选A。
2000-2024年AMC8真题和解析:2019年第8题

这道题的考点是百分数。
我们假设Gilda原来有100个玻璃球,那么第一次给出20%后,还剩100*(1-20%)=80个。第二次给出剩下的10%后,还剩:80*(1-10%)=72个。第3次给出剩下的25%后,还剩下:72*(1-25%)=54个,这占原来总数100个的54%,所以答案选E。
提醒:在比赛时,有的考生假设Gilda原来有玻璃球x个,然后把x代入计算,也能得出正确答案。不过这里直接假设100个是最快速的。要学会用这种假设、代数法。
2000-2024年AMC8真题和解析:2014年第11题

这道题考点是排列组合,我们先根据题意画出如下示意图。
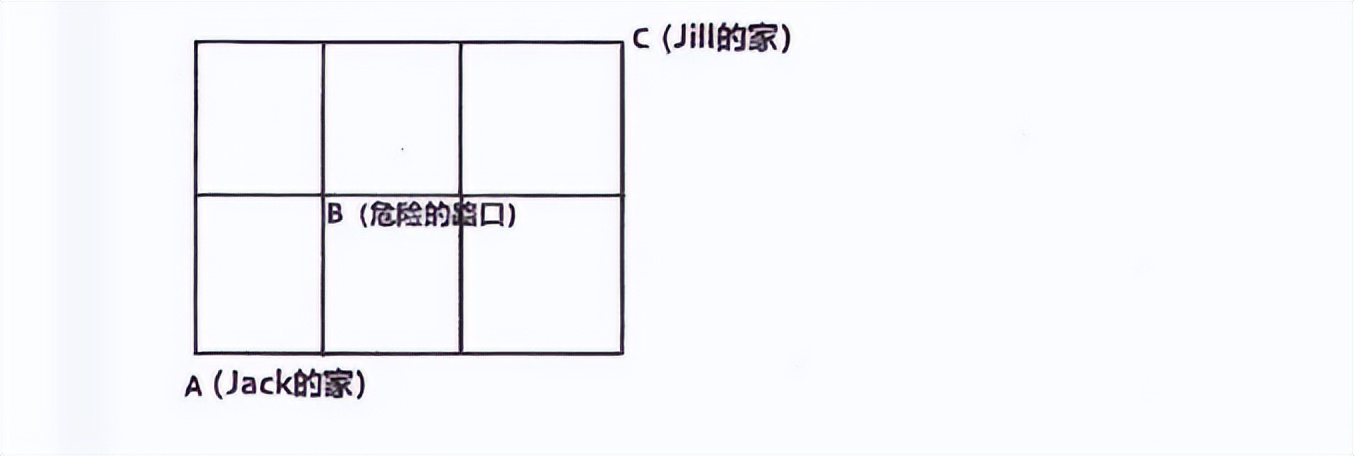
我们可以先算出经过这个危险的十字路口的方法数,然后将总方法数减去这个方法数,所得的差即为符合题意的方法数。
如上图所示,假设左下角A为Jack的家,右上角C点为Jill的家,B点为危险的十字路口。从A到B点共有2种方法,而从B到C,一共3种方法,因此从A经过B到C的路径共2*3=6条。而从A到C的总方法数为(包括经过B和不经过B)C(5,2)=10,因为从A到C共走5个街区,其中3个往东,2个往北,相当于是从5个位置中选择2个位置安排向北,剩下3个安排向东。因此不经过B的路径共有10-6=4条,答案选A。
提醒:在计算排列组合的题目时,从反面考虑,用总数减去反面情况得到我们所要的结果,这种方法很常见。
2000-2024年AMC8真题和解析:2012年第19题

这道题的考点是代数(列方程解应用题)。
根据题意,假设红色玻璃球有x个,绿色玻璃球有y个,蓝色玻璃球有z个,因为“除了6个之外的其他玻璃球都是红色的”,所以绿色+蓝色=y+z=6。同理,我们可以得到x+z=8,x+y=4。把这3个方程相加,得到2(x+y+z)=18,因此x+y+z=9,答案选C。
这道题目要注意审题,有的考生直接将三个数字相加答案算到了18,结果发现没有答案。(如果有个选项是18,估计很多人会掉坑了)。
2000-2024年AMC8真题和解析:2011年第4题

这道题的考点是数据分析(中位数,众数和平均数)
我们把这些数按照升序排列为:0,0,1,1,2,2,3,3,3。根据定义:平均数=(0+0+1+1+2+2+3+3+3)/9=15/9,观察数列可得中位数为2,众数为3。因为15/9<2<3,所以答案为C。
提醒:这几个概念和算法要熟悉,尤其是数列个数是偶数的时候如何计算中位数。
欢迎联系我免费获得高清完整版的600道AMC8试题和解析,欢迎免费体验独家、精心设计的在线真题练习集。
六分成长针对AMC8的高质量、科学的备考资源,欢迎了解更多
上述六分成长独家制作的在线练习题,符合学习和认知心理学,来源于完整的历年AMC8真题,并且会持续更新。AMC8备考可用,反复练习,也有利于小学、初中数学能力提升。还有配套的系统学习文档、视频资料赠送。

