动态网站建设有那些seo教程seo教程
做题方法:确定枚举顺序,画出递归树
递归实现指数型枚举
题目编号:
acwing.92.递归实现指数型枚举
题目描述:
从 1∼n 这 n 个整数中随机选取任意多个,输出所有可能的选择方案。
输入格式:
输入一个整数 n。
输出格式:
每行输出一种方案。
同一行内的数必须升序排列,相邻两个数用恰好 1 个空格隔开。
对于没有选任何数的方案,输出空行。
本题有自定义校验器(SPJ),各行(不同方案)之间的顺序任意。
数据范围:
1 ≤ n ≤ 15
输入样例:
3
输出样例:
3
2
2 3
1
1 3
1 2
1 2 3
递归树:
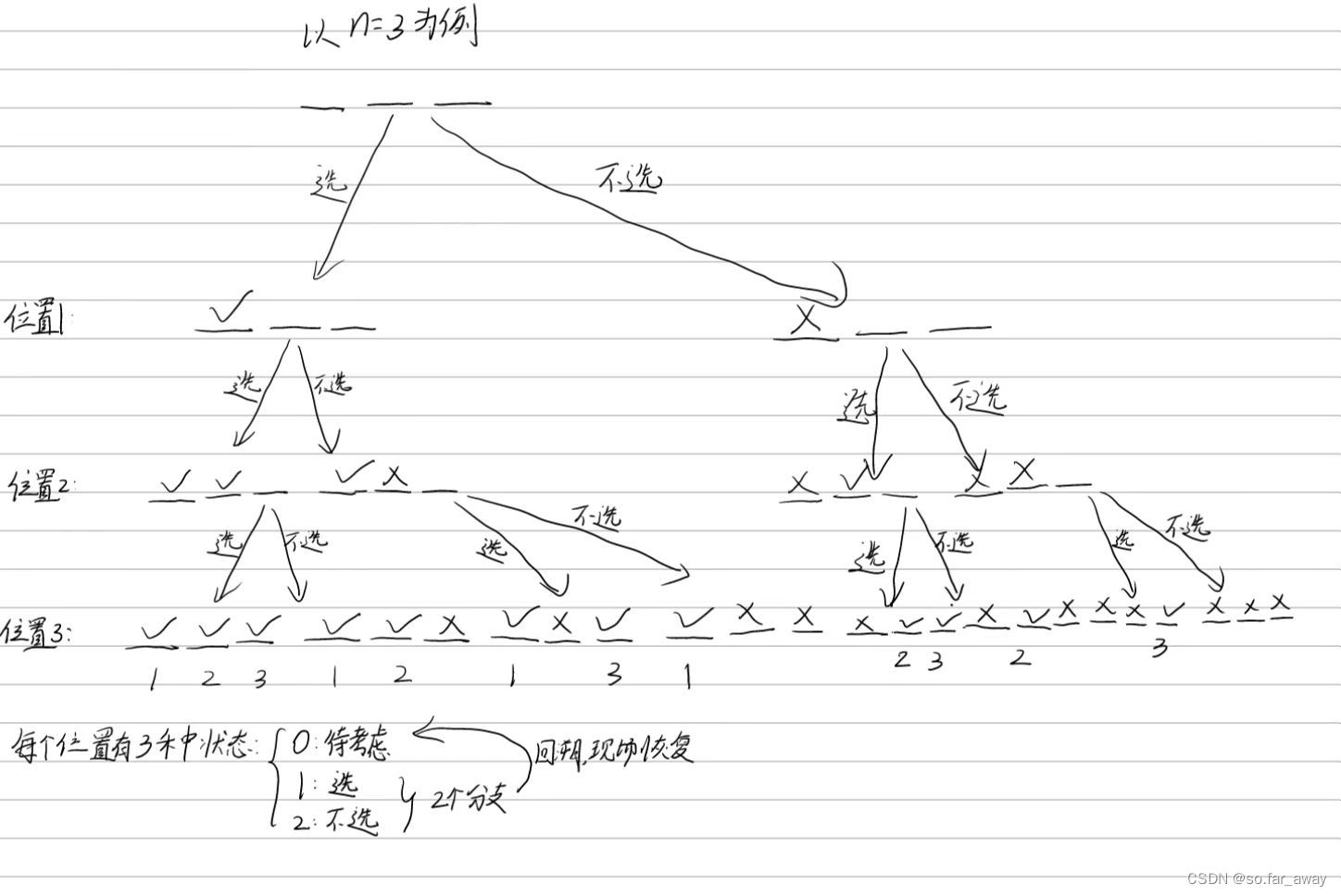
代码实现:
def dfs(i):global state,n#首先确定递归边界if i>n:for j in range(1,n+1):if state[j]==1:print(j,end=' ')print('')return#分支1:选state[i]=1dfs(i+1)#恢复状态state[i]=0#分支2:不选state[i]=2dfs(i+1)state[i]=0
n=int(input())
#共有三个状态:0表示待考虑 1表示选 2表示不选
state=[0 for i in range(n+1)]
#从第一个位置开始枚举
dfs(1)
原题链接:link
递归实现排列型枚举
题目编号:
acwing.94.递归实现排列型枚举
题目描述:
把 1∼n这 n 个整数排成一行后随机打乱顺序,输出所有可能的次序。
输入格式:
一个整数 n。
输出格式:
按照从小到大的顺序输出所有方案,每行 1 个。
首先,同一行相邻两个数用一个空格隔开。
其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面。
数据范围:
1 ≤ n ≤ 9
输入样例:
3
输出样例:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
递归树:
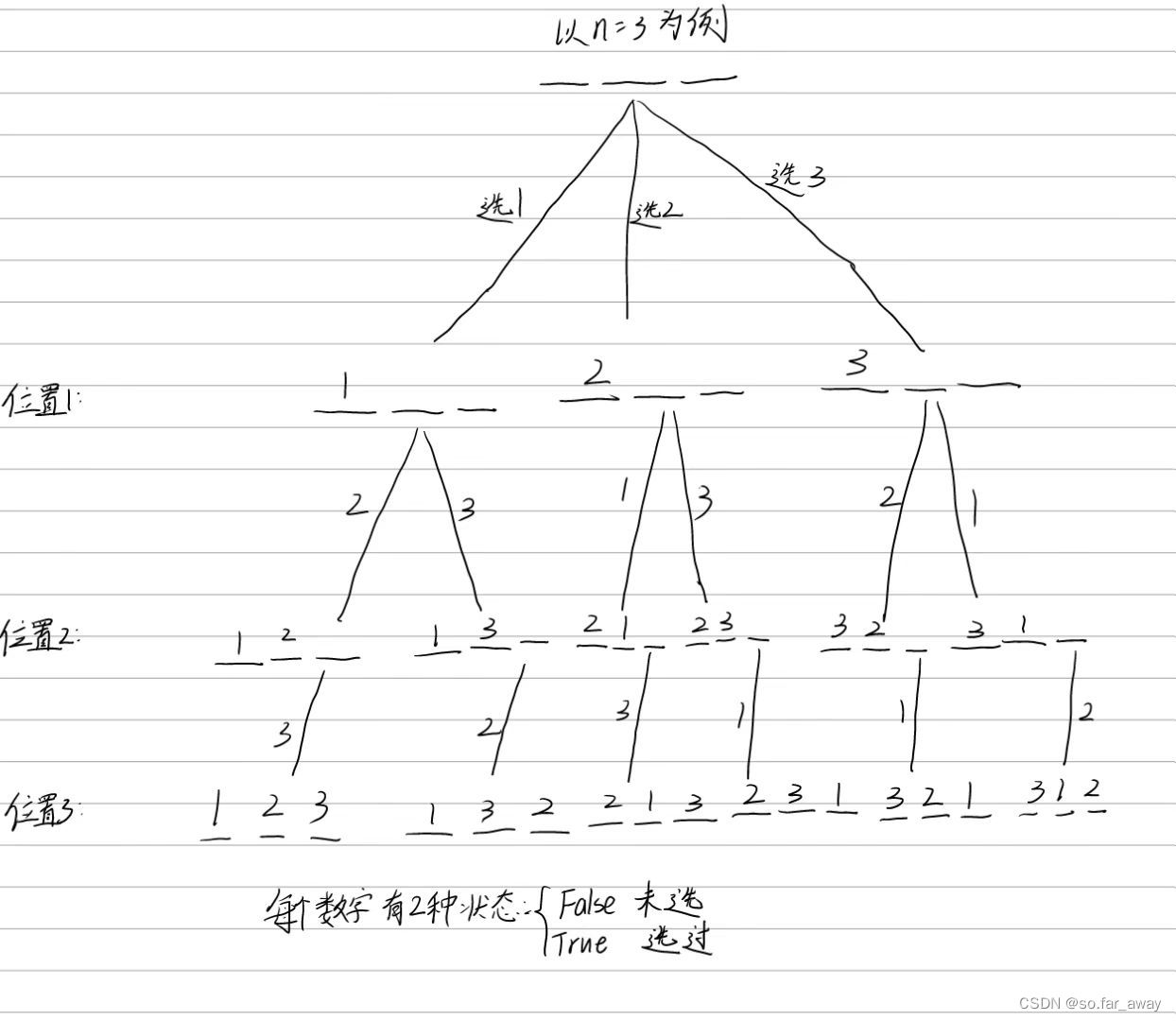
代码实现:
def dfs(i):global n,path,usedif i>n:for x in range(1,n+1):print(path[x],end=' ')print('')return#枚举每个分支,从小到大#即当前位置可以填哪个数for j in range(1,n+1):if used[j]==False:path[i]=jused[j]=Truedfs(i+1)path[i]=0used[j]=False
n=int(input())
#依次枚举每个位置都存哪个数
#path表示每个位置存的什么数
path=[0 for i in range(n+1)]
#used存每个数是否用过
used=[False for i in range(n+1)]
dfs(1)
原题链接:link
递归实现组合型枚举
题目编号:
acwing.93.递归实现组合型枚举
题目描述:
从 1∼n 这 n 个整数中随机选出 m 个,输出所有可能的选择方案。
输入格式:
两个整数 n,m ,在同一行用空格隔开。
输出格式:
按照从小到大的顺序输出所有方案,每行 1 个。
首先,同一行内的数升序排列,相邻两个数用一个空格隔开。
其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面(例如 1 3 5 7 排在 1 3 6 8 前面)。
数据范围:
n > 0,
0 ≤ m ≤ n ,
n+(n−m) ≤ 25
输入样例:
5 3
输出样例:
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
递归树:
与递归实现排列型枚举的递归树一样,只不过可选数字的范围变成1~n,每次选择的数字必须大于前边的数字,并且位数限制在m位。
代码实现:
升序考虑:
def dfs(i):global used,state,n,m,tmpif i>m:for i in range(1,m+1):print(state[i],end=' ')print('')return#保持升序选择#局部考虑 加限制条件#只需要保证新加的数大于前边的数即可for j in range(tmp,n+1):if used[j]==False:state[i]=jused[j]=Truetmp=jdfs(i+1)state[i]=0used[j]=False
n,m=map(int,input().split())
#每个数的状态 是否使用过
used=[False for i in range(n+1)]
#每个位置的状态 即每个位置填什么数
state=[0 for i in range(m+1)]
tmp=1
dfs(1)
降序考虑:
def dfs(i):global used,state,n,m,tmpif i>m:for i in range(1,m+1):print(state[i],end=' ')print('')return#保持降序选择#局部考虑#只需要保证新加的数小于前边的数即可for j in range(1,tmp+1):if used[j]==False:state[i]=jused[j]=Truetmp=jdfs(i+1)state[i]=0used[j]=False
n,m=map(int,input().split())
#每个数的状态 是否使用过
used=[False for i in range(n+1)]
#每个位置的状态 即每个位置填什么数
state=[0 for i in range(m+1)]
tmp=n
dfs(1)
原题链接:link
