上海公司网站设企业网址怎么申请
系列文章目录
- leetcode - 双指针问题_leetcode双指针题目-CSDN博客
- leetcode - 滑动窗口问题集_leetcode 滑动窗口-CSDN博客
- 高效掌握二分查找:从基础到进阶-CSDN博客
- leetcode - 前缀和_前缀和的题目-CSDN博客
- 动态规划 - 斐波那契数列模型-CSDN博客
- 位运算 #常见位运算总结 #题解-CSDN博客
- 模拟 - #介绍 #题解-CSDN博客
- leetcode - 分治-三路划分快速排序总结-CSDN博客
目录
系列文章目录
前言
1、题1 不同路径:
参考代码:
2、题2 不同路径 II:
参考代码:
3、题3 珠宝的最高价值:
参考代码:
4、题4 下降路径最小和 :
参考代码:
5、题5 最小路径和:
参考代码:
6、题6 地下城游戏 :
参考代码:
总结
前言
路漫漫其修远兮,吾将上下而求索;
大家可以先自己尝试做一下:
- 62. 不同路径 - 力扣(LeetCode)
- 63. 不同路径 II - 力扣(LeetCode)
- LCR 166. 珠宝的最高价值 - 力扣(LeetCode)
- 931. 下降路径最小和 - 力扣(LeetCode)
- 174. 地下城游戏 - 力扣(LeetCode)
在看篇博文之前建议先看博主的这一篇文章:动态规划 - 斐波那契数列模型_题目描述 禾木投出的弹珠在高低不平的泥路向坡底滚动着,坡上到坡底各处可以从1到n-CSDN博客
其中非常详细地阐述了整个动态规划地流程,本篇博文稍微简略些;
1、题1 不同路径:
62. 不同路径 - 力扣(LeetCode)

动态规划分为5步:
- 1、确定一个状态表达式
- 2、根据该状态表达式来推导状态转移方程
- 3、初始化
- 4、填表顺序
- 5、返回值
1.1 状态表达式
确定状态表达式要么是以某一个位置为结尾,要么是以某一个位置为起点;
一般根据我们的经验然后结合题干要求来确定该状态表达式;题干中让我们求出总共有多少条不同的路径,那么我们可以先尝试,dp[i][j] 表示走到 [i,j] 位置的时候一共有多少种方式;
1.2 状态转移方程
推导状态转移方程:1、用之前或者之后的状态推导得到dp[i] 的值 2、根据最近的一步来划分问题
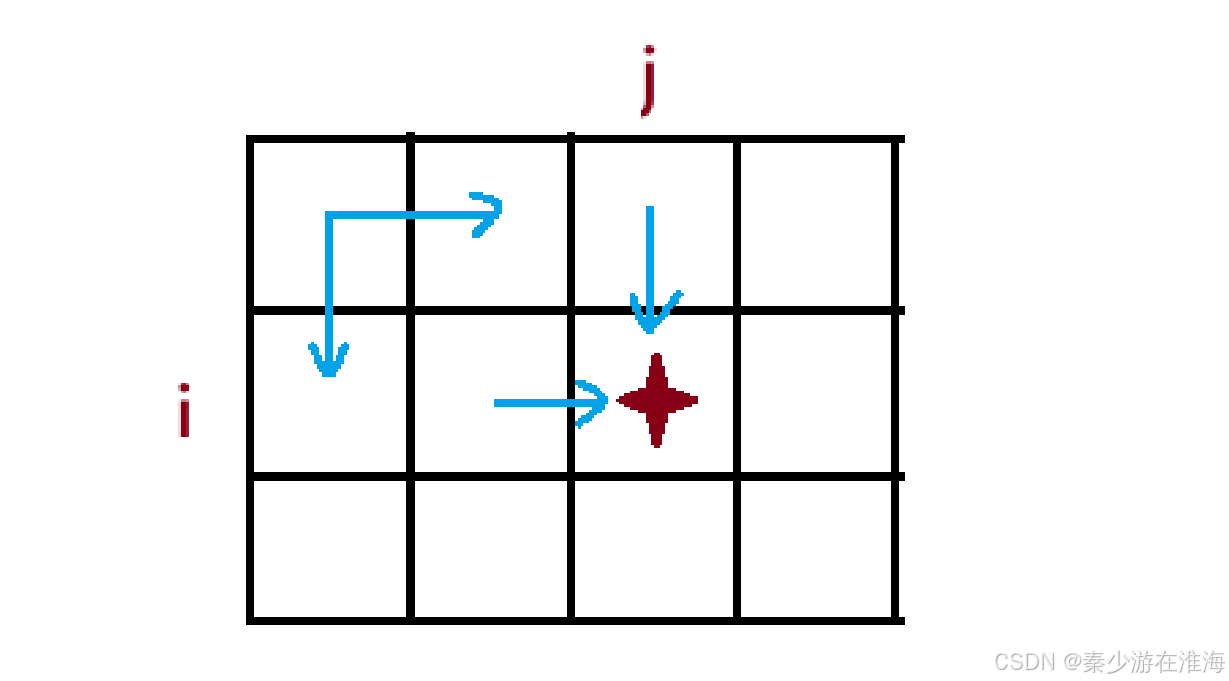
由于我们只能向左或者向下走,所以想要到达上图 [i][j] 位置,其上一步的状态只能是 [i-1][j] 或者 [i][j-1] ;
所以dp[i][j] 分为两种情况:一是从起点走到 [i-1][j] 然后往右走一步,走到 [i][j] ,那么从起点走到[i-1][j] 的方法数就是从[i-1][j] 走到 [i][j] 的方法数,即 dp[i][j] = dp[i-1][j] ;二是从起点走到 [i][j-1] 然后向下走一步到 [i][j] , 那么从起点走到[i][j-1] 的方法数就是从 [i][j-1] 走到 [i][j] 的方法数,即 dp[i][j] = dp[i][j-1];
所以 dp[i][j] = dp[i-1][j] + dp[i][j-1];
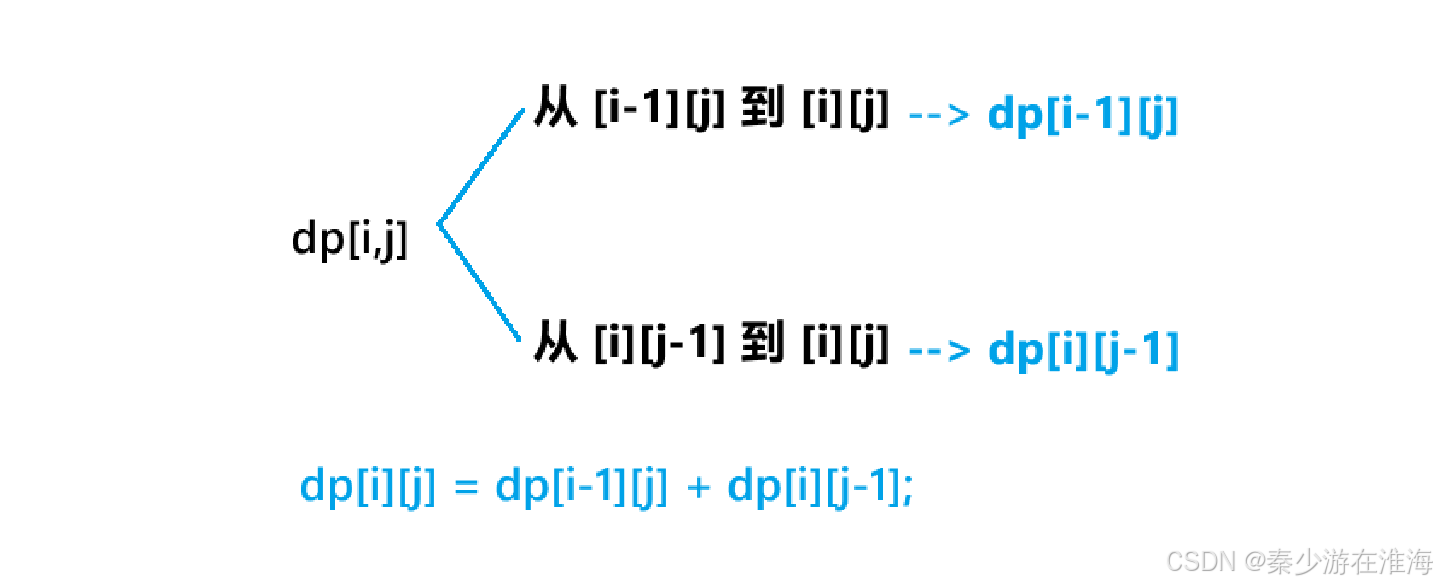
1.3 初始化
因为dp[i][j] = dp[i-1][j] + dp[i][j-1];要保证下标合法,就得让 i 、j 大于等于1;所以我们需要初始化第一行以及第一列;当然,如果我们在创建dp 表的时候多开辟了一行以及一列的空间,由于多了一行一列,那么在填表的时候就不会发生越界;
我们在创建 dp 表的时候,可以多开辟一行一列,避免越界的发生;但是需要有两点需要注意:
- 1、虚拟节点中的值(多开辟的空间)要保证填表的结果是正确的;
- 2、下标的映射关系;
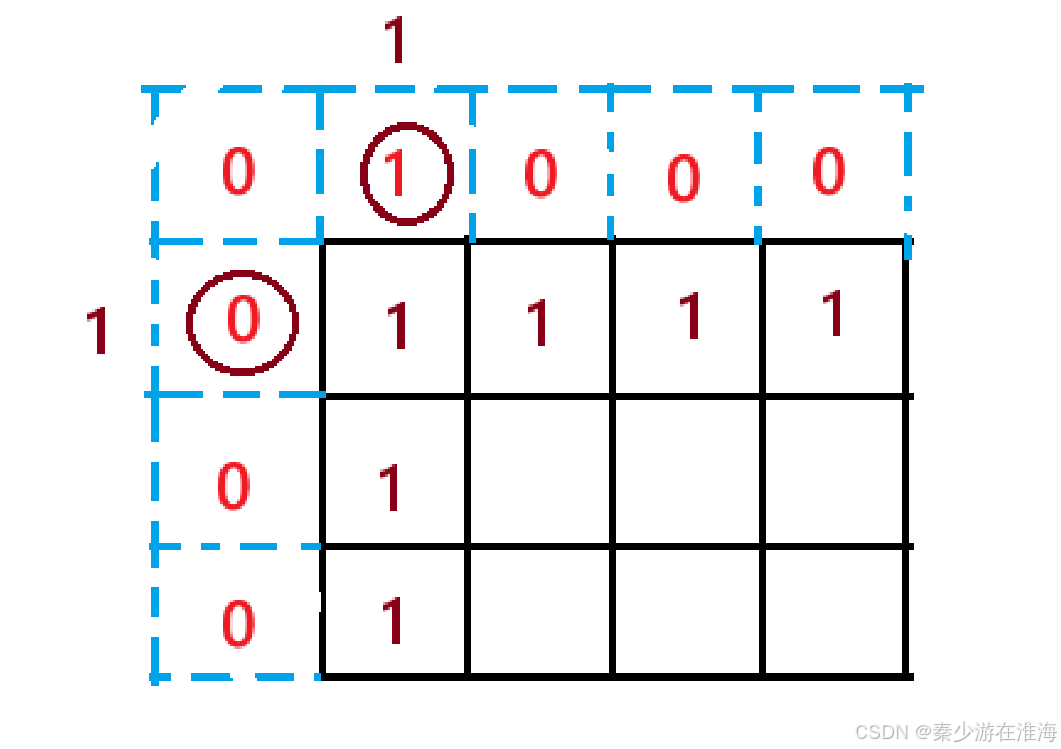
当dp 表多开辟一行一列的时候,需要保证下标为1的行以及下标为1的列中初始化的值均为1,而dp[1][1] = dp[i-1][j] + dp[i][j-1] ,所以我们需要确保dp[0][1] 或者 dp[1][0] 其中一个为1就可以了;其余的为0就行了;
1.4 填表顺序
- 为保证填写当前状态的时候所需要的状态已经计算好了;
从上往下,每一行从左往右;
1.5 返回值
返回结果: 结合题目要求+状态表示
假设所给二维数组有m行n列,那么dp[m][n] 就是题干所要的结果,直接返回即可;
参考代码:
int uniquePaths(int m, int n) {//状态表示 : dp[i][j] 走到[i][j] 的方法总数//状态转移方程:dp[i][j] = dp[i-1][j] + dp[i][j-1]//初始化:dp表多开辟一行一列,dp[1][0] = 1;//填表顺序:从上到下,从左往右;返回值 :dp[m][n]vector<vector<int>> dp(m+1, vector<int>(n+1));//初始化dp[1][0] = 1;//填表for(int i = 1;i<=m;i++){for(int j = 1;j<=n;j++){dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m][n];}2、题2 不同路径 II:
63. 不同路径 II - 力扣(LeetCode)
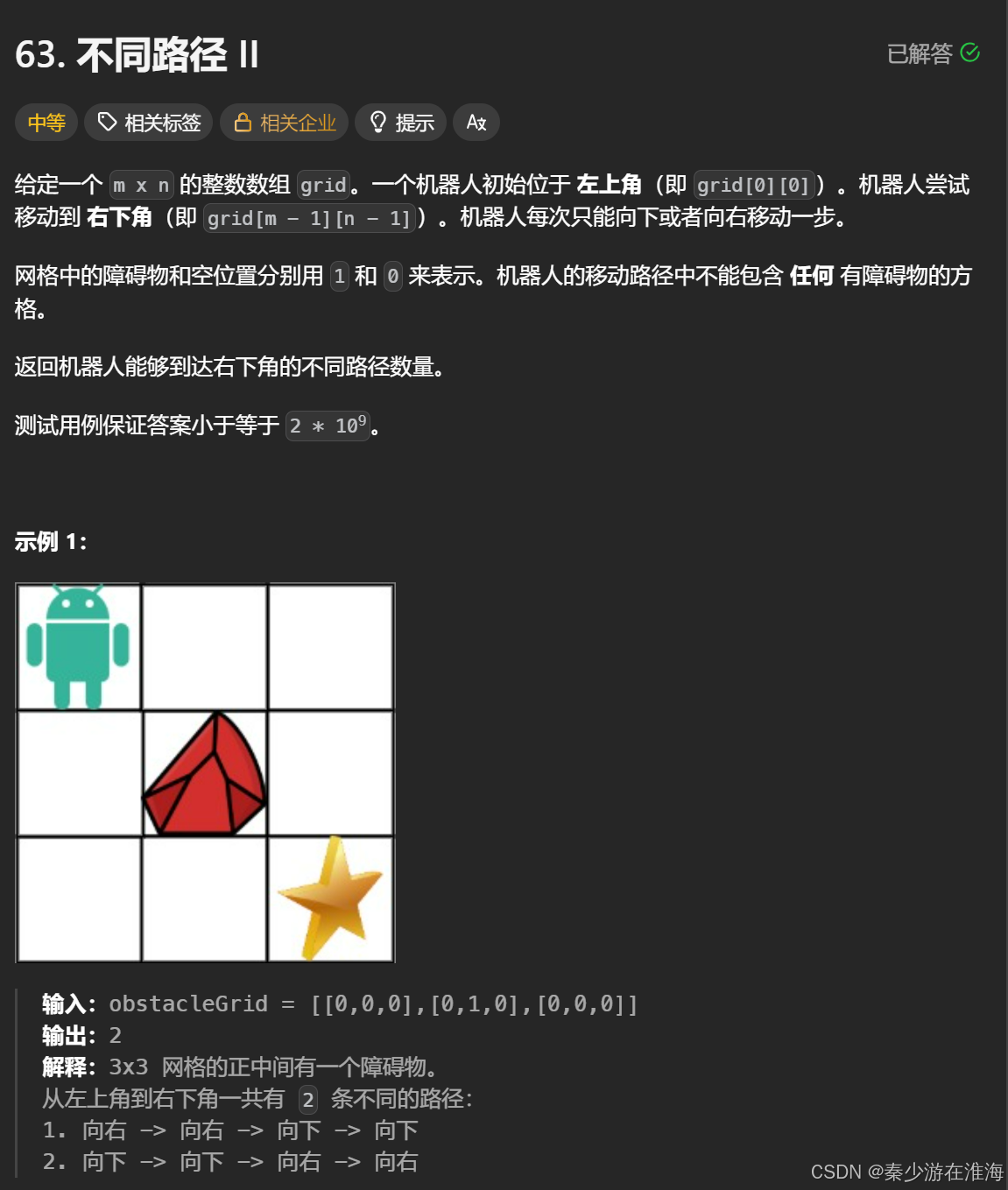
同样地,动态规划五部曲:
2.1 确定状态表示
确定状态表达式要么是以某一个位置为结尾,要么是以某一个位置为起点;
dp[i][j]: 到达 [i][j] 位置时,一共有多少种走法;
2.2 状态转移方程
因为本题中有障碍物,在填写dp表的时候还需要查看对应所给的二维数组中是否为障碍物,如果是障碍物,则 dp[i][j] = 0;如果不是障碍物,则dp[i][j] = dp[i-1][j] + dp[i][j-1] ;
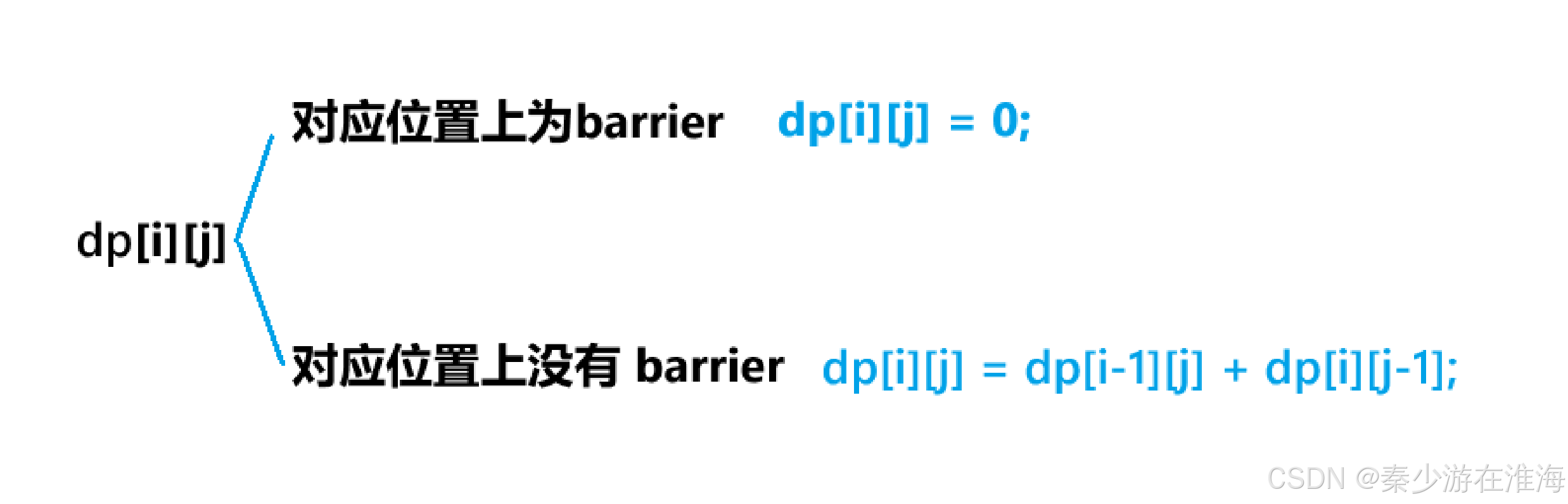
2.3 初始化
和上一题一样,dp 表可以多开辟一行一列来避免复杂的初始化;同时需要将dp[0][1] 或则dp[1][0] 初始化为1以保证接下来填表的正确性;
2.4 填表顺序
从上到下,从左往右
2.5 返回值
假设所给二维数组有m行n列,返回 dp[m][n] 即可;
参考代码:
int uniquePathsWithObstacles(vector<vector<int>>& nums) {int m = nums.size() , n = nums[0].size();vector<vector<int>> dp(m+1, vector<int>(n+1));//初始化dp[0][1] = 1;for(int i = 1;i<=m;i++){for(int j = 1;j<=n;j++){//注意下标的映射关系if(nums[i-1][j-1]) dp[i][j] = 0;else dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m][n];}3、题3 珠宝的最高价值:
LCR 166. 珠宝的最高价值 - 力扣(LeetCode)
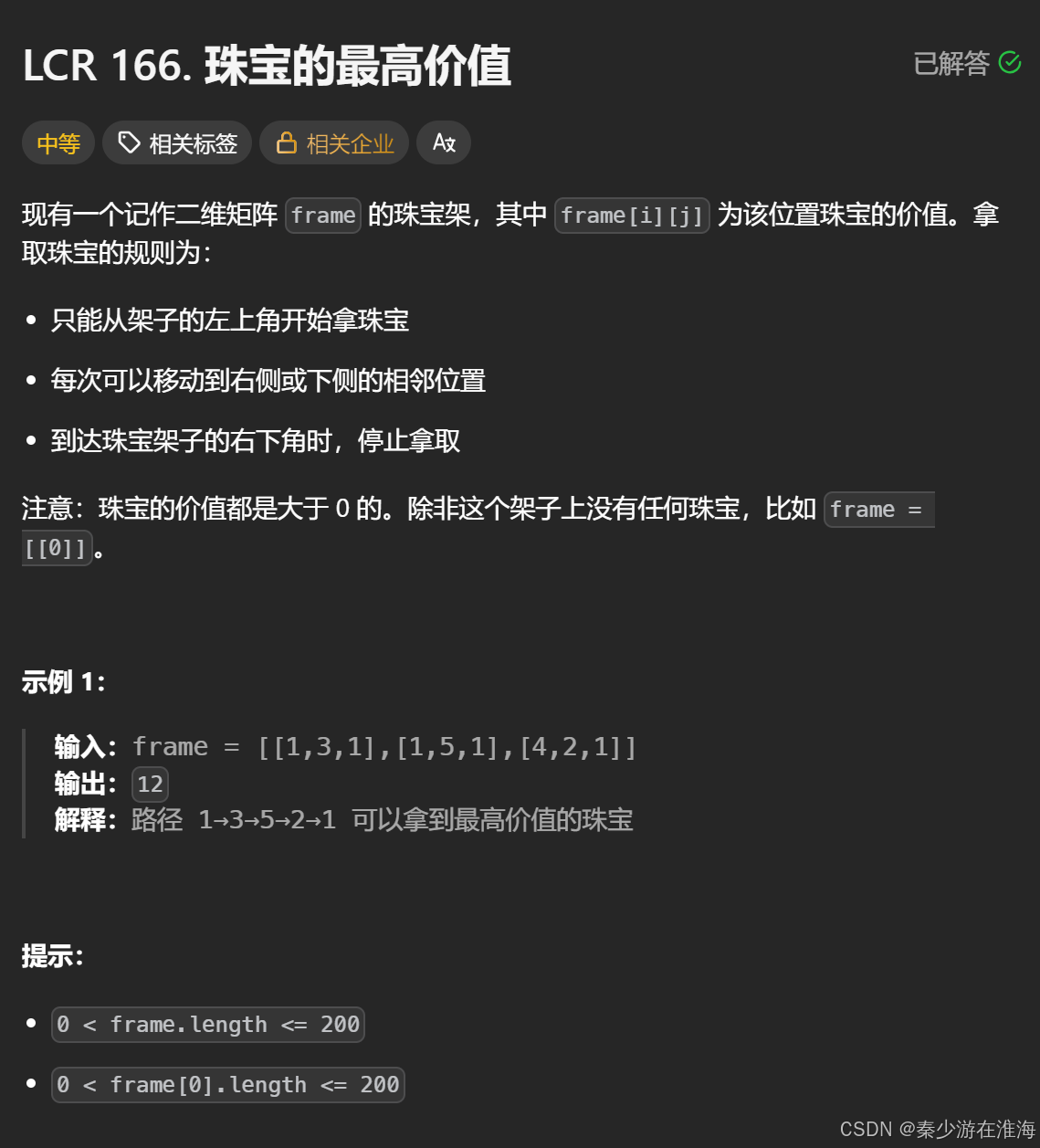
梳理:从左下角走到右下角,一步只能向右或者向下;求走到右下角价值最大;
同样地,动规五部曲:
3.1 确定状态表达式
确定状态表达式要么是以某一个位置为结尾,要么是以某一个位置为起点;
dp[i][j] : 到达 [i][j] 位置时的最大价值;
3.2 状态转移方程
因为到达 [i][j] 位置出发点有两种可能性,我们只要比较dp[i-1][j] 以及 dp[j][i-1] 谁大然后再加上这个位置上本身的价值;
所以 dp[i][j] = max(dp[i-1][j] , dp[i][j-1] ) + frame[i][j];
3.3 初始化
因为dp[i][j] = max(dp[i-1][j] , dp[i][j-1] ) + frame[i][j]; 为了避免越界问题,就得初始化dp表的第一行以及第一列;还可以将dp表多开一行以及多开一列来将初始化的过程简单化;
若我们将dp 表多开辟一行一列,就得保证初始化的值保证后面填表的正确性;观察动态表达式就可以发现,初始化为0就可以了;
- 1、虚拟节点中的值要保证填表的结果是正确的;
- 2、下标的映射关系;
3.4 填表顺序
从上往下,从左往右
3.5 返回值
假设所给二维数组有m行n列,返回 dp[m][n] 即可;
参考代码:
int jewelleryValue(vector<vector<int>>& frame) {int m = frame.size(), n = frame[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1));//不用初始化,默认开辟空间的时候就已经默认初始化为0for(int i = 1;i<=m;i++){for(int j = 1;j<=n;j++){//需要注意下标的映射关系dp[i][j] = max(dp[i-1][j] , dp[i][j-1]) + frame[i-1][j-1];}}return dp[m][n];}4、题4 下降路径最小和 :
931. 下降路径最小和 - 力扣(LeetCode)
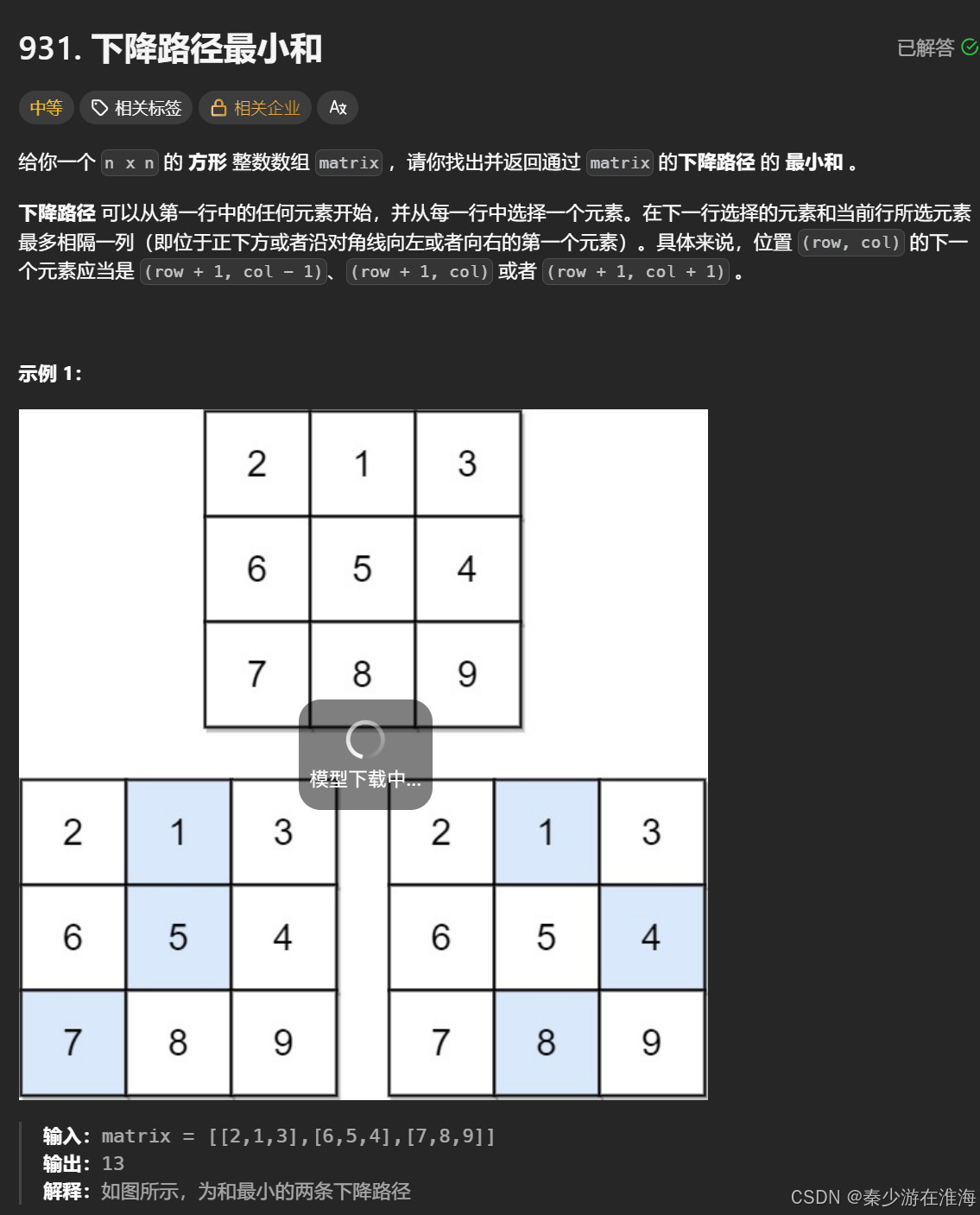
梳理:从第一行任意一个块开始到最后一行中任意一个块中,每次向下(对角线向右、直向下、对角线向左)走一步;求最小和;
动态规划五部曲:
4.1 确定状态表示
确定状态表达式要么是以某一个位置为结尾,要么是以某一个位置为起点;
根据我们的经验以及题目要求;
dp[i][j]: 下降到位置 [i][j] 的最小和;
4.2 状态转移方程
推导状态转移方程:1、用之前或者之后的状态推导得到dp[i][j] 的值 2、根据最近的一步来划分问题
根据最后一步来分析;
如何到达 [i][j] 的位置呢?要么从 [i-1][j] 下来,要么从[i-1][j-1] 下来,要么从 [i-1][j+1] 下来;在这三种情况中取最小值然后加上 nums[i][j] 即可;
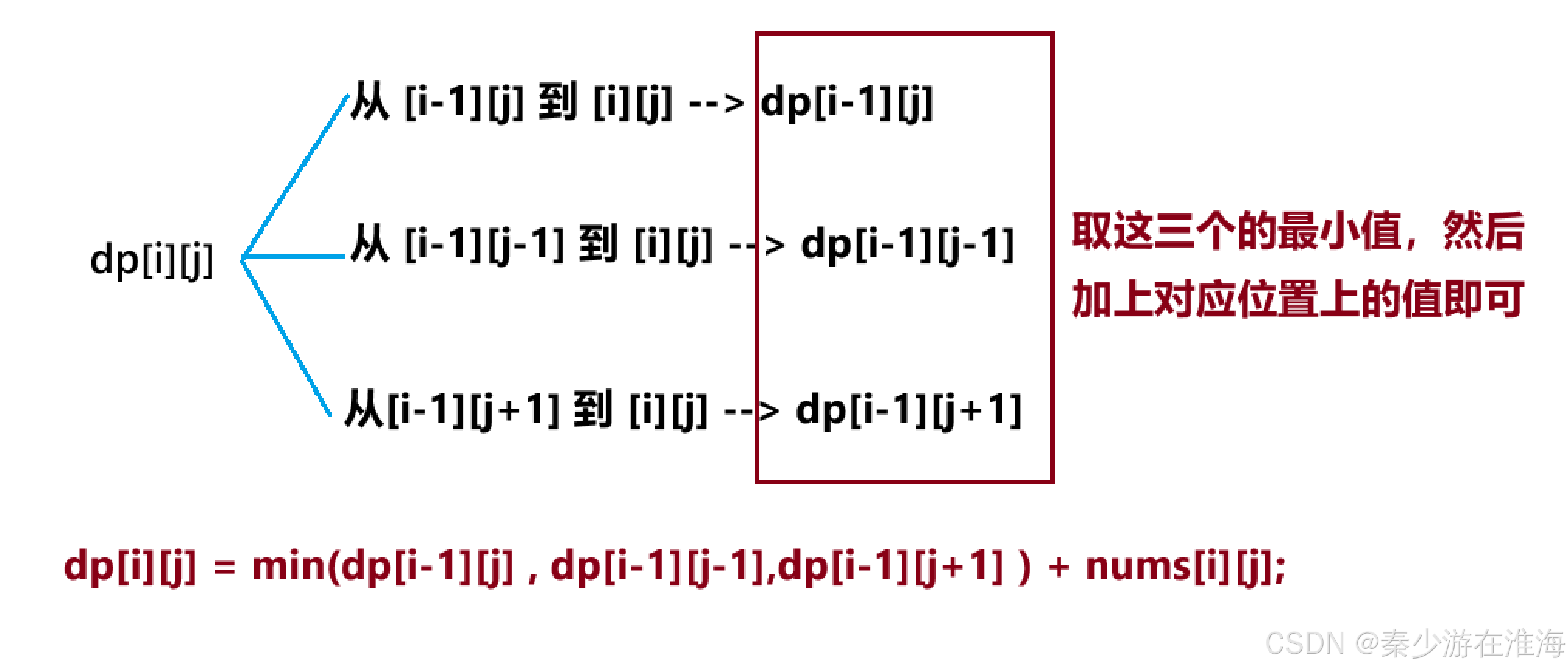
4.3初始化
为了在填表的过程中不会发生越界访问的情况;
观察状态转移返程可知,为了使得下标合法就需要初始化第一行以及第一列,这样处理初始化有点繁琐;当然了,做了以上的题到了这里也非常明了,我们还可以多增加一行一列来辅助初始化;
dp 表多开辟了一行一列有两点需要我们注意:
- 1、里面的值要保证后面填表的正确性
- 2、下标的映射
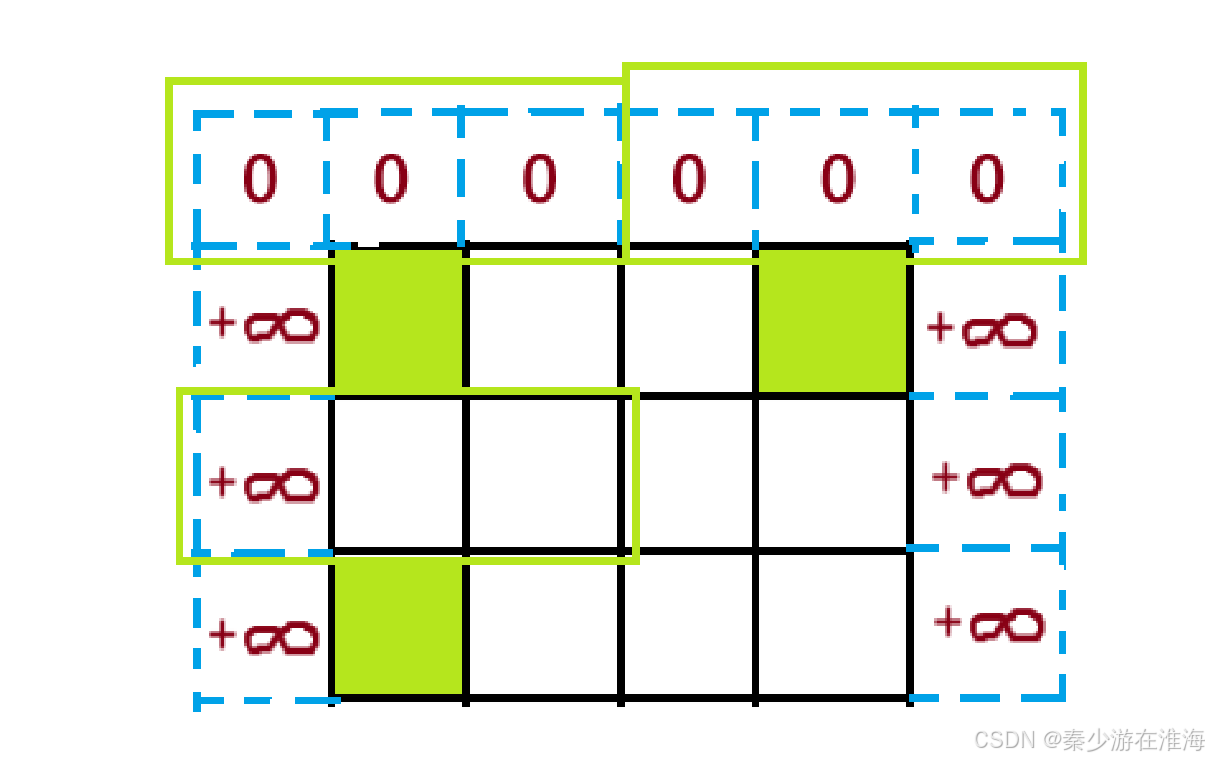
观察第一行第一个和最后一个点可以发现,由于本题求一个点最小和的时候,会用到该点斜左上方、正上方、斜右上方的值;为了避免越界就需要多开辟一行两列;第一行初始化为0,其他初始化为INT_MAX;
4.4 填表顺序
从上往下
4.5 返回值
因为最后一个落点我们是不知道的,返回dp表中最后一行的最小值即可;
参考代码:
int minFallingPathSum(vector<vector<int>>& matrix) {int m = matrix.size() , n = matrix[0].size();vector<vector<int>> dp(m+1,vector<int>(n+2,INT_MAX));//初始化,第一行初始化为0for(int i = 0;i<=m+1;i++) dp[0][i] = 0;//填表for(int i = 1;i<=m;i++){for(int j = 1;j<=n;j++){//需要注意下标的映射关系dp[i][j] = min(dp[i-1][j] , min(dp[i-1][j-1] , dp[i-1][j+1])) + matrix[i-1][j-1];}}//在dp 表的最后一行中找到最小值int ret = INT_MAX;for(int i = 1;i<=n;i++) ret = min(ret , dp[m][i]);return ret;}5、题5 最小路径和:
64. 最小路径和 - 力扣(LeetCode)

梳理:从左上角到右下角,每次只能向下或者向右走一步;求达到右下角的最小和;
动态规划五部曲:
5.1 确定状态表达式
确定状态表达式要么是以某一个位置为结尾,要么是以某一个位置为起点;
dp[i][j] : 走到 [i][j] 位置时的最小和;
5.2 状态转移方程
根据最后一步进行推导;到达 [i][j] 位置的上一步有两种情况,一是从 [i-1][j] 向下走一步到达 [i][j] ,二是从 [i][j-1] 向右走一步到达 [i][j];求这两种情况的最小值然后加上当前 [i][j] 位置上的值即可;

5.3 初始化
观察状态转移方程,为了避免越界,就需要初始化dp 表得第一行以及第一列;还有一种处理方式来规避越界问题,dp表多开辟一行以及一列;需要注意的是,多开辟的空间需要保证dp表后续填表的正确性,以及下标的映射关系;
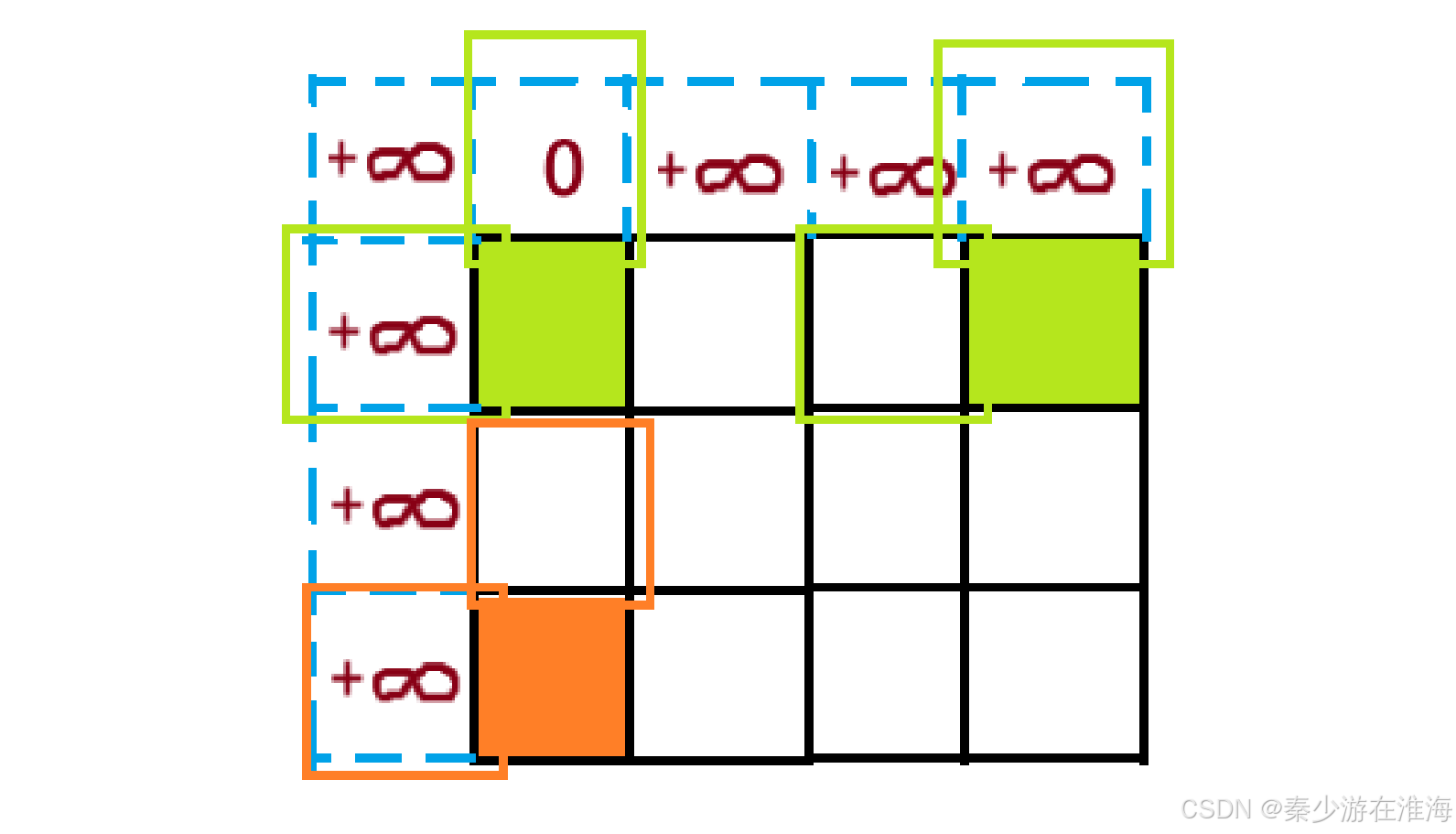
为了不影响后续填表的正确性,dp表多开辟一行一列之后需要将 dp[0][1] 或者 dp[1][0] 的位置初始化为1,其他位置初始化为 INT_MAX;
5.4 填表顺序
从上到下,从左往右
5.5 返回值
返回 dp[m][n]
参考代码:
int minPathSum(vector<vector<int>>& grid) {int m =grid.size(), n = grid[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));//初始化dp[0][1] = 0;//填表for(int i = 1;i<=m;i++){for(int j = 1;j<=n;j++){//注意下标地映射关系dp[i][j] = min(dp[i-1][j] , dp[i][j-1]) + grid[i-1][j-1];}}return dp[m][n];}6、题6 地下城游戏 :
174. 地下城游戏 - 力扣(LeetCode)

梳理:从左上角走到右下角,每次只能向下或者向右走一步;要求在这过程中,和不能小于等于0,求起始值的最小值;
动态规划五部曲;
6.1 确定状态表达式
状态表达式,一般是以某一个位置为起点或者某一个位置为结尾;
如果以某一个位置为结尾:dp[i][j] 表示走到 [i][j] 位置,所需的最低初始健康点数;动一下我们聪明的小脑袋都可以知道,如果以某一个位置为结尾,从前往后走,如何求得初始的最低健康点数?显然,本题应该从后往前走:以某一个位置为起点,dp[i][j] 表示从[i][j] 位置开始出发,到达终点所需要的最低的健康点数;
6.2 状态转移方程
根据状态表达式,推导状态转移方程:1、用之前或者之后的状态推导得到dp[i] 的值 2、根据最近的一步来划分问题;
从 [i][j] 位置到终点,接下来有两种走法,一是向右走,二是向下走;在这两种情况中选择消耗的最小值,然后减去当前位置[i][j] 的消耗;
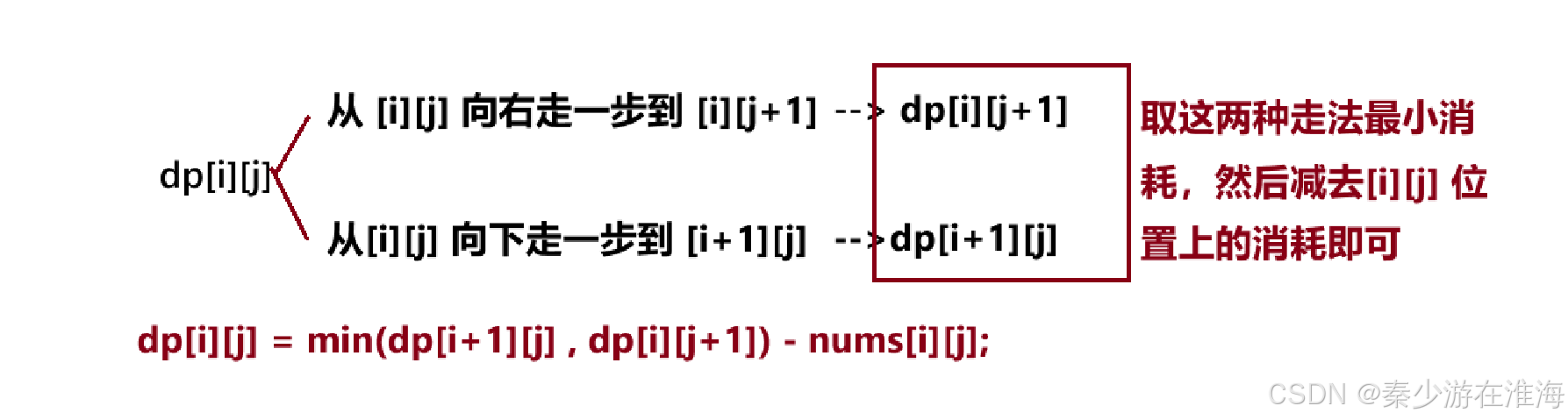
6.3 初始化
此处我们为dp 表多开辟一行一列的空间,并且需要保证多开辟的空间不会影响我们后续填表的正确性;
保证 i+1 、j+1 不会越界,所以多开辟的一行一列为最后一行最后一列;
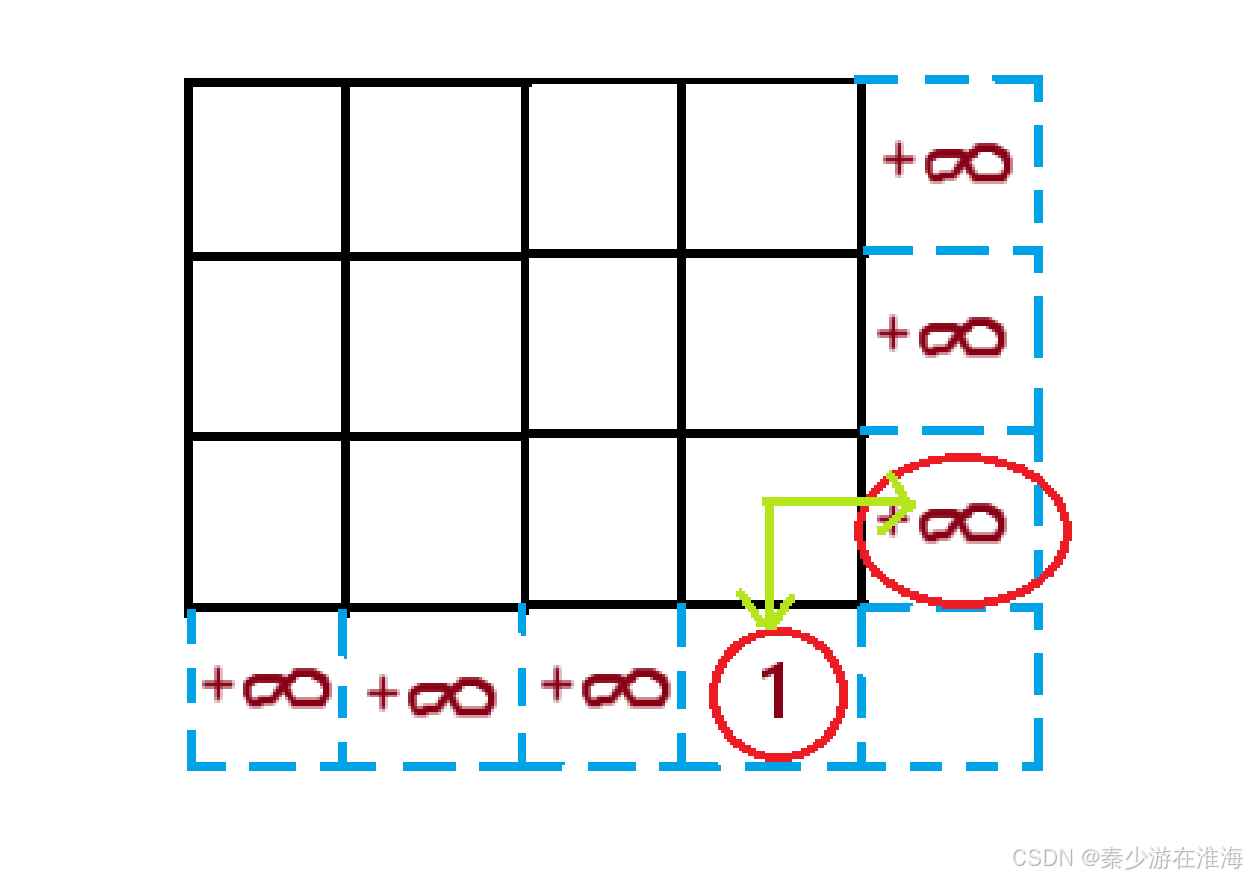
当以 [m-1][n-1] 为起点的时候,要么向右走,要么向左走,取这两种走大的最小值;因为值为0就意味着骑士噶了,所以将 dp[m][n-1] 或者 dp[m-1][n] 初始化为1即可;其余的初始化为INT_MAX;
但dp[i][j] = min(dp[i+1][j], dp[i][j+1]) - nums[i][j] 结果可能为负数,为了让骑士活着,当值为负数的时候,手动设置当前的生命值为 1;即 dp[i][j] = max(1,dp[i][j]);
6.4 填表顺序
因为本题的状态转移方程依靠后面且靠右的状态,所以填表顺序为每一列从下往上,每一行从右往左;
6.5 返回值
dp[0][0]
参考代码:
int calculateMinimumHP(vector<vector<int>>& dungeon) {int m = dungeon.size() , n = dungeon[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1 , INT_MAX));//初始化dp[m-1][n] = 1;//填表for(int i = m-1;i>=0;i--){for(int j = n-1;j>=0;j--){dp[i][j] = min(dp[i+1][j] , dp[i][j+1]) - dungeon[i][j];dp[i][j] = max(1,dp[i][j]);//可能为负数}}return dp[0][0];}总结
动态规划五个步骤:
- 1、确定一个动态表达式
- 2、根据该动态表达式来推导状态转移方程
- 3、初始化
- 4、填表顺序
- 5、返回值
一般有三种方式可以来确定状态表示:
1、题目怎么要求,我们就怎么定义状态表示
2、经验 + 题目要求
3、分析题目的过程中发现重复的子问题(再将重复的子问题抽象为状态表达式)
推导状态转移方程:1、用之前或者之后的状态推导得到dp[i] 的值 2、根据最近的一步来划分问题;
初始化的目的:保证填dp表(根据状态转移方程来调表)的时候不会发生越界;
填表顺序的目的是为了保证在填表的时候,所要依据的状态已经存在了;
