网站内页做友情链接微信营销的特点

前言

对于全排列问题，常用的做法是设置一个vis数组来确定位置i上的数字是否被访问，因为是全排列问题，所以不同的顺序也是不一样的排列，因此每次都是从起点开始询问**(注意起点到底是0还是1)**

46全排列(最简单的模板)

class Solution {
public:vector<int>v;//存储一个排列vector<vector<int>>ans;//答案int vis[10];void dfs(vector<int> & nums){int n = nums.size();if(v.size() == n){ans.push_back(v);return;}for(int i = 0; i < n; i++){if(vis[i])continue;vis[i] = 1;v.push_back(nums[i]);dfs(nums);v.pop_back();vis[i] = 0;}}vector<vector<int>> permute(vector<int>& nums) {dfs(nums);return ans;}};

解题思路

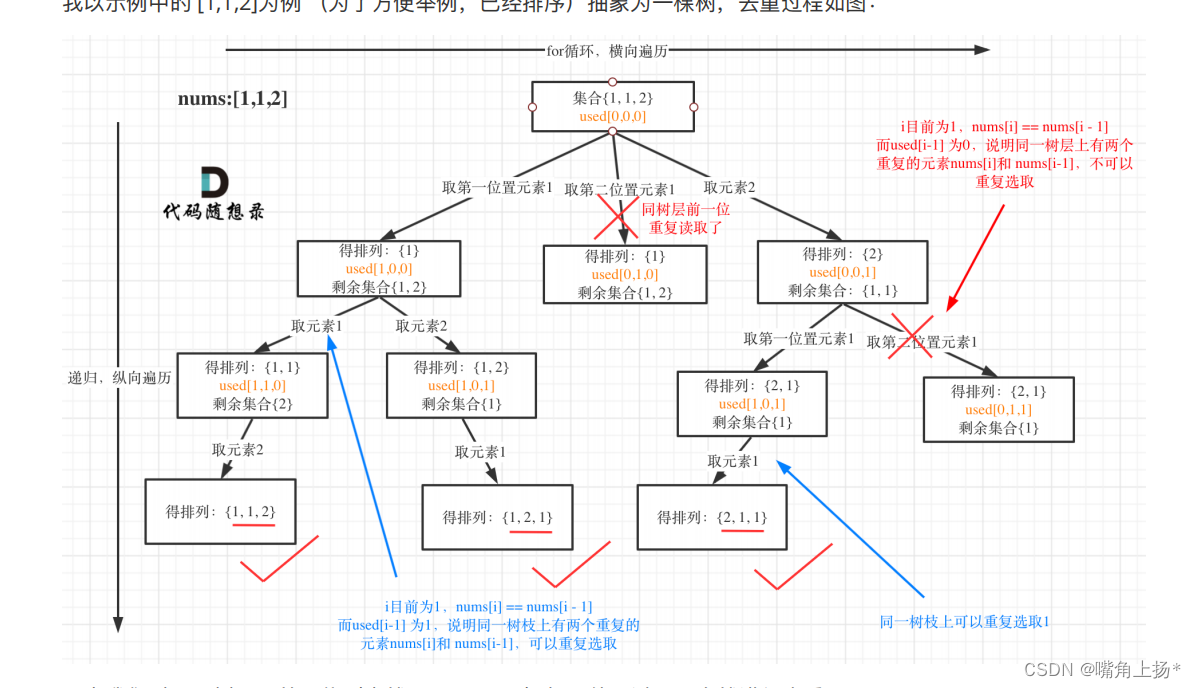
相比于全排列1，全排列2增加了重复数字，但要求不能出现重复的排列。例如原始序列1 2 1 那么全排列里 1 1 2 和 1 1 2 （两个序列的两个1位置互换了），仍然当一种排列。最好的办法就是对其进行剪枝

  if(i > 0 && nums[i] == nums[i - 1] && vis[i - 1] == 0) continue;//树层去重

借鉴卡哥的一幅图，给大家看一下

（类似题目）P8605 [蓝桥杯 2013 国 AC] 网络寻路

#include<iostream>
#include<algorithm>
#include<string>
#include<vector>
#include<stack>
#include<cstdio>
#define rep(i,a,n) for(int i = a; i <= n; i++) 
#define per(i,a,n) for(int i = n; i >= a; i--)using namespace std;typedef long long ll;const int N = 10010;
vector<int> v[N];
int vis[N];
int n,m;
ll ans;
vector<int>st;
void dfs(int x){int n = v[x].size();if(st.size() == 3){//因为终点位置可以和起点相同，所以当路径元素为3个的时候，就开始特判 rep(i,0, n - 1){int tp = v[x][i];if(!vis[tp] || tp == st[0]) ans++;//没被访问或者是起点 }return ;}rep(i,0,n-1){int tp = v[x][i];if(!vis[tp]){vis[tp] = 1;st.push_back(tp);dfs(tp);st.pop_back();vis[tp] = 0;}}
}int main(){cin >> n >> m;int u,vv;rep(i,1,m){cin >> u >> vv;v[u].push_back(vv);v[vv].push_back(u);}rep(i,1,n){vis[i] = 1;st.push_back(i);dfs(i);vis[i] = 0;st.pop_back();}cout << ans;return 0;}

16全排列2

//leetcode
class Solution {
public:vector<int> v;vector<vector<int>>ans;int vis[10];vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(),nums.end());dfs(nums);return ans;}void dfs(vector<int>& nums){int n = nums.size();if(v.size() == n){ans.push_back(v);return;}for(int i = 0; i < n; i++){if(vis[i])continue;if(i > 0 && nums[i] == nums[i - 1] && vis[i - 1] == 0) continue;//树层去重vis[i] = 1;v.push_back(nums[i]);dfs(nums);v.pop_back();vis[i] = 0;}}
};

解题思路

经典的回溯问题，但分解开来看就很简单了

1 初始化:

vector<vector<string>> ans;//答案
vector<string> v(n,string(n,'.'));//二维矩阵存图，vector是一个数组，每个数组元素又是string类型，所以可以看成C语言里char类型的二维数组

2. 按行进行DFS递归

void dfs(int u, int n,vector<string>& v){//u代表下标为u的行if(u == n){ans.push_back(v);return;}for(int i = 0; i < n; i++){if(check(u,i,n,v)){v[u][i] = 'Q';dfs(u + 1, n,v);v[u][i] = '.';}}}

3 根据题目条件判断：不能同行 同列 同斜线，同行问题不会出现，因为咱们是按照行来递归遍历的，所以只需要判断同列 同斜线问题

int check(int x, int y,int n,vector<string> &v){for(int i = 0; i < x; i++){if(v[i][y] == 'Q') return 0;}for(int i = x - 1, j = y - 1; i >= 0&&j >= 0; i--, j--){if(v[i][j] == 'Q') return 0;}for(int i = x - 1, j = y + 1; i >= 0 && j <= n; i--,j++){if(v[i][j] == 'Q') return 0;}return 1;}

n皇后

class Solution {
public:vector<vector<string>> ans;vector<vector<string>> solveNQueens(int n) {vector<string> v(n,string(n,'.'));dfs(0,n,v);return ans;}int check(int x, int y,int n,vector<string> &v){for(int i = 0; i < x; i++){if(v[i][y] == 'Q') return 0;}for(int i = x - 1, j = y - 1; i >= 0&&j >= 0; i--, j--){if(v[i][j] == 'Q') return 0;}for(int i = x - 1, j = y + 1; i >= 0 && j <= n; i--,j++){if(v[i][j] == 'Q') return 0;}return 1;}void dfs(int u, int n,vector<string>& v){if(u == n){ans.push_back(v);return;}for(int i = 0; i < n; i++){if(check(u,i,n,v)){v[u][i] = 'Q';dfs(u + 1, n,v);v[u][i] = '.';}}}
};

22.括号生成

class Solution {
public:vector<string>ans;//dfs搜索规则// 先放左括号，左括号数量lc < n, 则放// 然后如果左括号数量大于右括号数量且右括号数量rc < n,则放右括号void dfs(int lc, int rc, int n, string s){if(lc == n && rc == n){ans.push_back(s);return;}if(lc < n) dfs(lc + 1, rc, n, s + '(');if(lc > rc && rc < n) dfs(lc, rc + 1, n , s + ')');}vector<string> generateParenthesis(int n) {dfs(0,0,n,"");return ans;}
};

79. 单词搜索

class Solution {//主要思想:id标记下一个待寻找的字母，不是的话直接不寻找，vis作为标记走过的路径，不能回头走（例三）
public:int vis[10][10];//标记使用过的位置bool flag = false;int dx[4] = {0,0,1,-1};int dy[4] = {1,-1,0,0};void dfs(string & s,vector<vector<char>>& g,int u, int v,int id){if(flag) return;if(id == s.size()){flag = true;return;}for(int i = 0; i < 4; i++){int x = u + dx[i];int y = v + dy[i];//v写成u了，卡了一阵if(x >= 0 && x < g.size() && y>= 0 && y < g[0].size() && g[x][y] == s[id]){if(vis[x][y] == 1)continue;vis[x][y] = 1;dfs(s,g,x,y,id + 1);vis[x][y] = 0;}}}bool exist(vector<vector<char>>& board, string word) {for(int i = 0; i < board.size(); i++)for(int j = 0; j < board[0].size(); j++){if(board[i][j] == word[0]){vis[i][j] = 1;dfs(word,board,i,j,1);vis[i][j] = 0;}}return flag;}
};