邯郸房地产网站建设重庆专业seo
文章目录
- 格中取模运算
- CVP和格的陪集
- 致谢
格中取模运算
定义(格的基本区域) P⊂Rn:{P+x∣x∈L}\mathcal{P} \subset \mathbb{R}^n : \{ \mathcal{P} + \bm{x} | \bm{x} \in \mathcal{L} \}P⊂Rn:{P+x∣x∈L}是Rn\mathbb{R}^nRn的一种划分。
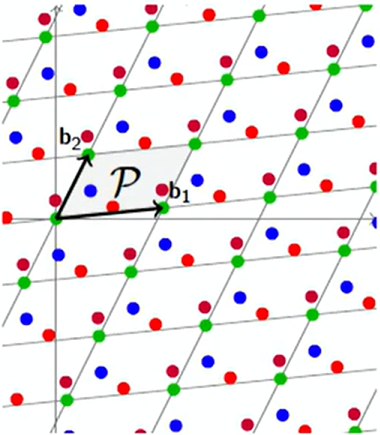
用P\mathcal{P}P对格点取模会呈现周期规律,即很多点“值”重复,例如上图中的绿色点为一组、红色点为一组、蓝色点为一组、棕色点为一组等。
- (L,+)(\mathcal{L}, +)(L,+)是(Rn,+)(\mathbb{R}^n, +)(Rn,+)的子群;
- 根据第1点可以构造商群Rn/L\mathbb{R}^n / \mathcal{L}Rn/L,念作RnmodL\mathbb{R}^n ~ \mathrm{mod} ~ \mathcal{L}Rn mod L;
- 对于Rn/L\mathbb{R}^n / \mathcal{L}Rn/L中的元素,与该元素同组的元素,共同构成一个陪集t+L\bm{t} + \mathcal{L}t+L;
- 格中每一个基本区域都提供了一套格和陪集的标准表示法。
商群和陪集的概念乍一看很迷惑,但其实很好理解,请参考文章
- 【群论入门】(5): 子群、陪集、正规子群与商群(收录于机器学习的数学基础)
- 商群 - 百度百科

注意: 这里格的基本区域P\mathcal{P}P取半开区域,以上图二维格为例,可以是左边界、下边界为闭边界,而右边界、上边界为开边界,这样格中的所有点就均只属于一个基本区域,即每个陪集在每个基本区域中也只有一个点。
- P=∑ibi⋅[0,1)≡Rn/L\mathcal{P} = \sum_i \bm{b}_i \cdot [0, 1) \equiv \mathbb{R}^n / \mathcal{L}P=∑ibi⋅[0,1)≡Rn/L。
由于对格进行取模,故t+L\bm{t} + \mathcal{L}t+L又可表示为(B∨)t(mod1)(\bm{B}^\vee) \bm{t} ~ (\mathrm{mod} ~ 1)(B∨)t (mod 1)。注意,由于t+L\bm{t} + \mathcal{L}t+L不在格上,故对偶空间基向量乘以该点结果不会是整数,除以1必然有小数部分,而这个小数部分可以独立地代表不同的商群。(个人疑问: 这里的mod\mathrm{mod}mod物理意义理解起来感觉怪怪的,为什么是小数部分?推测可能是计算机实际上没有整除这一功能,除以1还是会有小数部分;或者就是为了表示起来简单方便,用模1表示取小数部分)
如何求对偶格基上一篇文章给出了参考答案:格密码学习笔记(五):对偶格。
CVP和格的陪集
利用格陪集,CVP可以有另外一种定义方式。这里公开课视频讲得有点抽象,我尝试写笔记结合推测解释一下。
定义(CVP) 给定一个格陪集t+L\bm{t} + \mathcal{L}t+L,在该格陪集中找到距离原点最近的点。
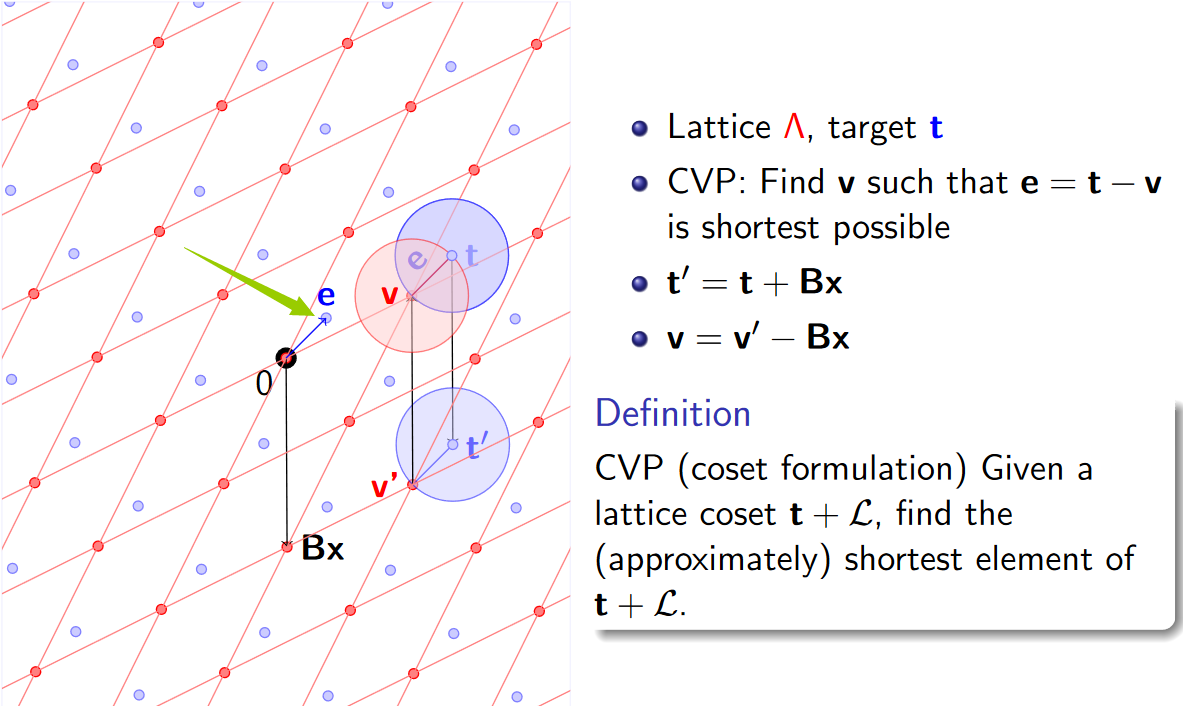
以上图为例,对于CVP给定的点t\bm{t}t,利用对偶格基相乘再模1可以获取陪集t+L\bm{t} + \mathcal{L}t+L中的所有点,即浅粉色的那部分点,找到距离原点最近的浅粉色点(绿色箭头所指),则t−e\bm{t} - \bm{e}t−e即CVP问题的解。
致谢
- Simons格密码公开课官网
Mathematics of Lattices - Simons Institute for the Theory of Computing - 哔哩哔哩中英双语视频(字幕组:重庆大学大数据与软件学院 后量子密码研究小组)
【中英字幕】Simons格密码讲座第1讲:格的数学定义_哔哩哔哩_bilibili - 其它格密码讲解课程和博文
Lattice学习笔记03:Dual Lattice(对偶格)
公开学习资料的无私奉献者
