手机h5网站模板下载比较开放的浏览器

归并排序

算法思路

归并排序算法有两个基本的操作，一个是分，也就是把原数组划分成两个子数组的过程。另一个是治，它将两个有序数组合并成一个更大的有序数组。

将待排序的线性表不断地切分成若干个子表，直到每个子表只包含一个元素，这时，可以认为只包含一个元素的子表是有序表。
将子表两两合并，每合并一次，就会产生一个新的且更长的有序表，重复这一步骤，直到最后只剩下一个子表，这个子表就是排好序的线性表。

代码

// 归并排序
public int[] sortArray(int[] nums) {return mergeSort(nums, 0, nums.length - 1);
}private int[] mergeSort(int[] nums, int left, int right) {// 递归终止条件if (left >= right) {// 返回单个元素的数组return new int[]{nums[left]};}// 分治int mid = (left 0+ right) / 2;// 分别对左右子数组进行排序int[] leftArr = mergeSort(nums, left, mid);int[] rightArr = mergeSort(nums, mid + 1, right);int[] res = new int[leftArr.length + rightArr.length];// 合并两个有序数组int i = 0, j = 0, k = 0;while (i < leftArr.length && j < rightArr.length) {if (leftArr[i] <= rightArr[j]) {res[k++] = leftArr[i++];} else {res[k++] = rightArr[j++];}}while (i < leftArr.length) {res[k++] = leftArr[i++];}while (j < rightArr.length) {res[k++] = rightArr[j++];}return res;
}

时间复杂度

O(nlogn)

堆排序

什么是堆？

如下图（大根堆）（二叉）堆是一个数组，它可以被看成一个完全二叉树。
二叉树形式：

数组形式：

堆的根节点在数组中的下标为0，我们很容易得到左孩子为1，右孩子为2，第i个节点的左孩子为2i+1，右孩子为2i+2 。
二叉堆分为两种形式：大根堆和小根堆。大根堆性质，根节点的值大于所以子树节点的值。小根堆性质，根节点的值小于所以子树节点的值。

如何维护堆？

Java代码维护大根堆：

//维护大根堆
private void heapify(int n,int i) {//当前根节点int largest = i;//左孩子节点int lchild = 2*i+1;//右孩子节点int rchild = 2*i+2;//找三个元素最大的作为父节点if (lchild < n && nums[lchild] > nums[largest]) {largest = lchild;}if (rchild < n && nums[rchild] > nums[largest]) {largest = rchild;}//如果交换则维护交换后的if (largest != i) {swap(largest,i);heapify(n,largest);}
}

问题：为啥交换后，只需要维护交换后的子节点呢？
举一个例子：

根节点需要跟左孩子交换，交换后，根节点的右子树并未改变树结构，则只需要递归维护根节点左子树的堆性质。

如何建堆？

我们可以用自低向上的方法利用上面维护堆的算法heapify来建堆。子数组从n/2开始都是树的叶子节点。每个叶子节点可以被看成包含一个元素的堆。所以建堆的过程从n/2-1–>0 。

//1.建堆//从最后一个有孩子的节点开始 n/2-1for (int i = n/2-1; i >= 0; i--) {heapify(n,i);}

堆排序

前面我们利用建堆算法成功建立一个大根堆。因为数组最大元素总在根节点nums[0]中，通过把它与nums[n-1]交换，我们可以让该元素放到正确的位置。这时候，如果我们从堆中去掉节点n-1，剩余节点中根的孩子结点仍然是大根堆，而新的根节点可能违背大根堆性质。为了维护大根堆性质，需要不断调用 heapify 从而在nums 上构建一个新的大根堆。堆排序算法会不断重复这个过程，直到堆的大小从n-1降到1 。

给出完整的堆排序算法：

private int[] nums;// 待排序数组
//堆排序									
private void heap_sort(int n) {//1.建堆//从最后一个有孩子的节点开始 n/2-1for (int i = n/2-1; i >= 0; i--) {heapify(n,i);}//2.堆排序for (int i = n-1; i > 0; i--) {swap(i,0);//交换最后一个和根元素heapify(i,0);//交换后维护}
}
//维护大根堆
private void heapify(int n,int i) {int largest = i;int lchild = 2*i+1;int rchild = 2*i+2;//找三个元素最大的作为父节点if (lchild < n && nums[lchild] > nums[largest]) {largest = lchild;}if (rchild < n && nums[rchild] > nums[largest]) {largest = rchild;}//如果交换则维护交换后的if (largest != i) {swap(largest,i);heapify(n,largest);}
}private void swap(int i,int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;
}

时间复杂度

O(nlogn)

快速排序

算法思想

通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
快速排序算法通过多次比较和交换来实现排序，其排序流程如下：

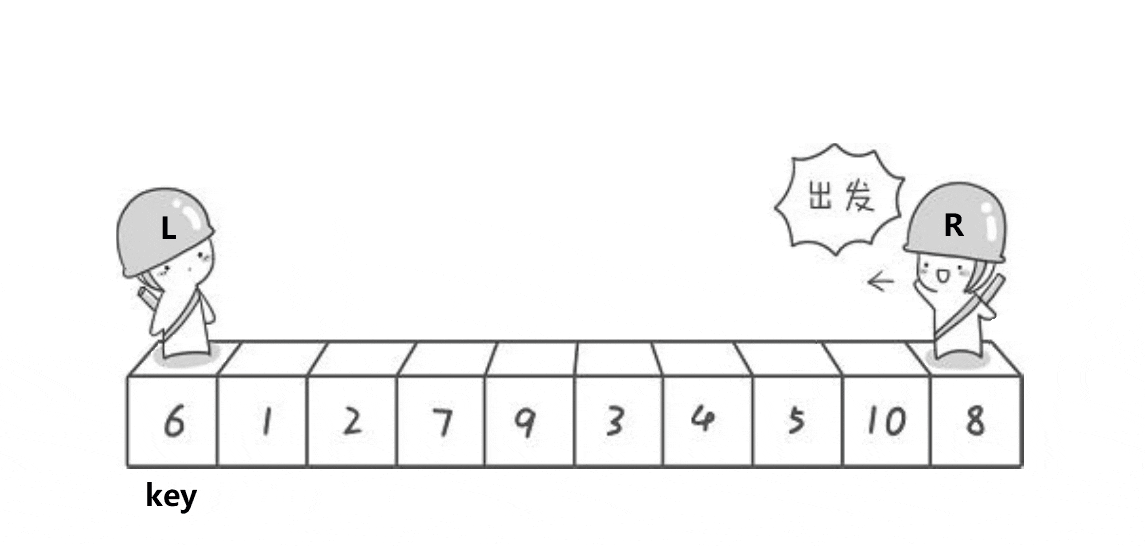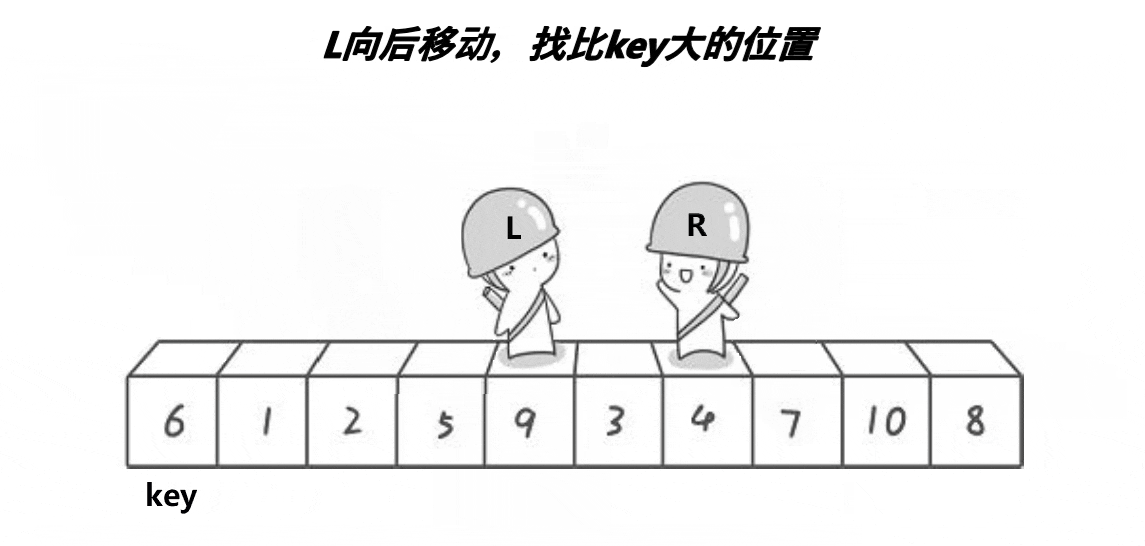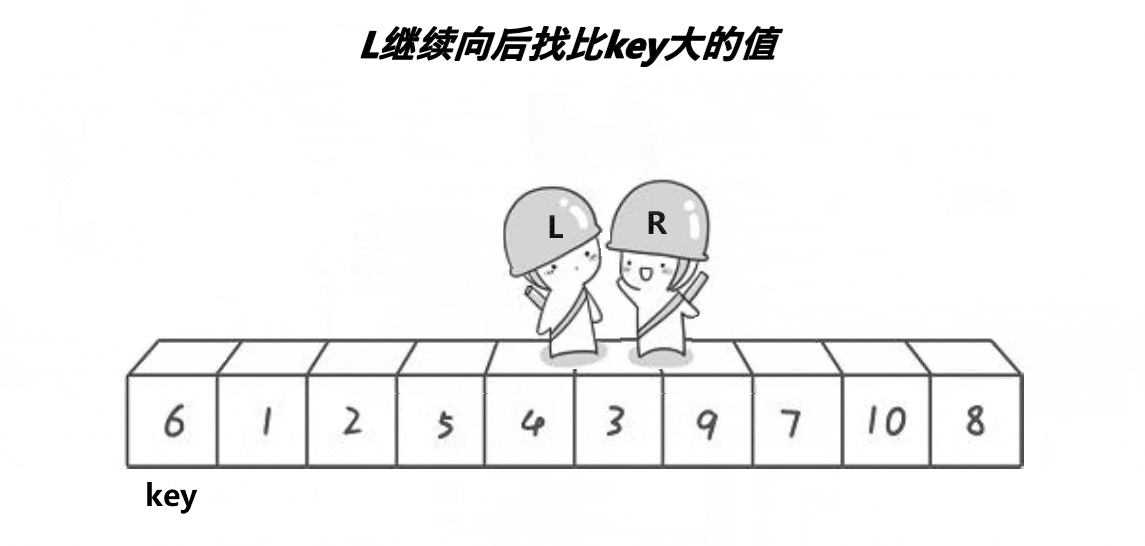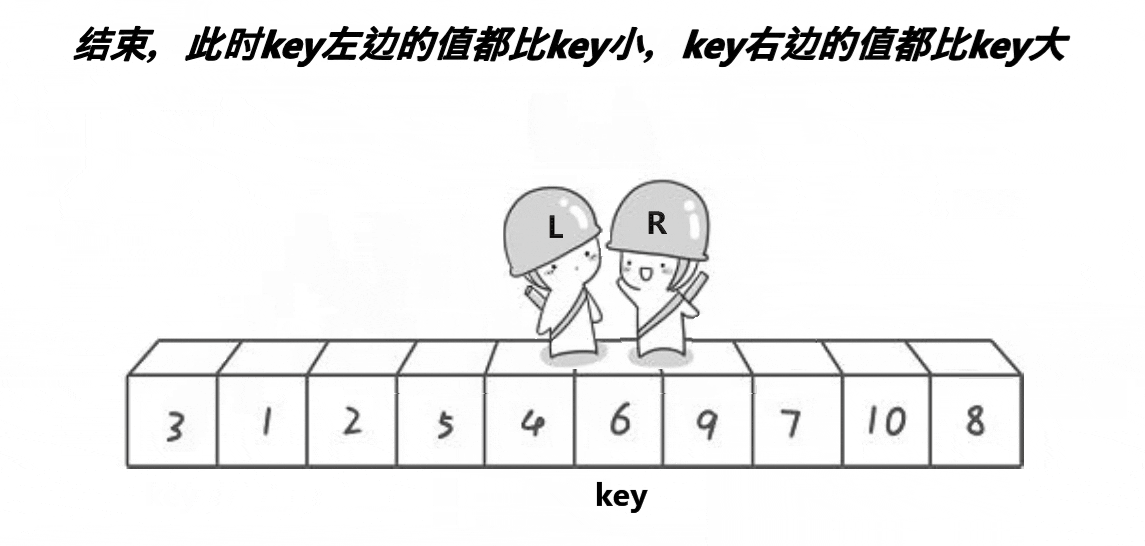
1、首先设定一个基数，通过该基数将数组分成左右两部分。

2、将大于或等于基数的数据集中到数组右边，小于基数的数据集中到数组的左边。此时，左边部分中各元素都小于或等于基数，而右边部分中各元素都大于或等于基数。

3、然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个基数，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。

4、重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

概括来说为 挖坑填数 + 分治法。

代码

代码中使用Random作为随机生成器生成基数，思想不变，只是基数选取的方式改变。

private int[] nums;
// 随机数生成器, 用于生成选择基数元素
private final Random random = new Random();public int[] sortArray(int[] nums) {this.nums = nums;quickSort(0, nums.length - 1);return nums;
}
public void quickSort(int left, int right) {// 递归终止条件if (left >= right) {return;}// 调用partition函数，对数组进行分区，并获取基准元素的最终位置int pivot = partition(left, right);// 递归调用，对左子数组进行快速排序quickSort(left, pivot - 1);// 递归调用，对右子数组进行快速排序quickSort(pivot + 1, right);
}
public int partition(int left, int right) {// 生成一个随机的基准元素位置int pivot = random.nextInt(right - left + 1) + left;// 保存基准元素的值int pivotVal = nums[pivot];// 将基准元素交换到数组的最后一个位置swap(pivot, right);// 定义两个指针，i指向数组的最左边，j指向数组的最右边int i = left, j = right;while (i < j) {// 从左向右找到第一个大于等于基准元素的位置while (i < j && nums[i] <= pivotVal) {i++;}// 从右向左找到第一个小于等于基准元素的位置while (i < j && nums[j] >= pivotVal) {j--;}// 如果i和j指向的位置不合法，则交换i和j指向的元素if (i < j) {swap(i, j);}}// 将基准元素交换到正确的位置swap(i, right);return i;
}public void swap(int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;
}

时间复杂度

O(nlogn)