嘟嘟嘟在线观看日本seo页面内容优化
目录
数独
"四独"游戏
解的存在和唯一性
算法
常微分方程
数独
采用蛮力试凑法来解决数独问题。(采用单选数,以及计算机科学技术中的递推回溯法)
以上的数独是图14-2的两个矩阵的和,左侧的矩阵可以由kron和magic函数建立起来,前一个函数用来求Kronecker乘积,后者生成幻方矩阵。
X = kron(eye(3), magic(3))
"四独"游戏
使用4×4网格,可能的备选项用小数标注出来。将单选数填在网格内,如果没有单选数,则采用递归回溯法来求解。(左:有单选数; 右:无单选数)
X=diag(1:4)Y=shidoku(diag(1:4)) Z=shidoku(diag(1:4)')' %可能的另一个解
解的存在和唯一性
可以用sudoku_all程序来寻找数独全部的解。
%生成数独谜题 X=kron(eye(3), magic(3)) X=sudoku_puzzle(13)数独网格的一些运算可能改变其在图形用户界面中的显示,但不能改变其基本特性。所有变化基本上都是相同的数字谜。这些等效的运算可以用matlab的数组运算表示。
%重新排列表示数字的文字 p = randperm(9), z=find(X>0). X(z)=p(X(z)) %其它运算 X', rot90(X, k) flipud(X), fliplr(X),X([4:9 1:3], :) X(:, randperm(3) 4:9)
function L = sudoku_all(X,L)
% SUDOKU_ALL Enumerate all solutions to a Sudoku puzzle.
% L = sudoku_all(X), for a 9-by-9 array X, is a list of all solutions.
% L{k} is the k-th solution.
% L{:} will print all the solutions.
% length(L) is the number of solutions. A valid puzzle must have only one.
% See also sudoku, sudoku_basic, sudoku_puzzle, sudoku_assist.if nargin < 2% Initialize the list on first entry.L = {};end% Fill in all "singletons", the cells with only one candidate.% C is the array of candidates for each cell.% N is the vector of the number of candidates for each cell.% s is the index of the first cell with the fewest candidates.[C,N] = candidates(X);while all(N>0) & any(N==1)s = find(N==1,1);X(s) = C{s};[C,N] = candidates(X);end% Add a solution to the list.if all(X(:)>0)L{end+1} = X;end% Enumerate all possible solutions.if all(N>0)Y = X;s = find(N==min(N),1);for t = [C{s}] % Iterate over the candidates.X = Y;X(s) = t; % Insert a value.L = sudoku_all(X,L); % Recursive call.endend% ------------------------------function [C,N] = candidates(X)% C = candidates(X) is a 9-by-9 cell array of vectors.% C{i,j} is the vector of allowable values for X(i,j).% N is a row vector of the number of candidates for each cell.% N(k) = Inf for cells that already have values.tri = @(k) 3*ceil(k/3-1) + (1:3);C = cell(9,9);for j = 1:9for i = 1:9if X(i,j)==0z = 1:9;z(nonzeros(X(i,:))) = 0;z(nonzeros(X(:,j))) = 0;z(nonzeros(X(tri(i),tri(j)))) = 0;C{i,j} = nonzeros(z)';endendendN = cellfun(@length,C);N(X>0) = Inf;N = N(:)';end % candidates
end % sudoku_all
算法
基本流程:
① 填入所有的单选数
②如果某个单元没有备选项,停止程序
③在某个空白的网格中填入一个试探的值
④ 递归式调用此程序
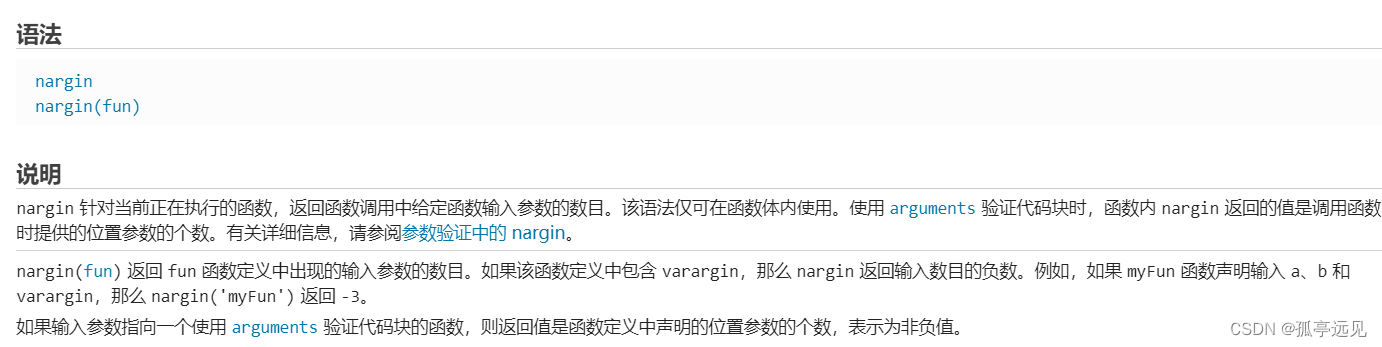
function [X,steps] = sudoku(X,steps)
% SUDOKU Solve a Sudoku puzzle using recursive backtracking.
% sudoku(X), for a 9-by-9 array X, solves the Sudoku puzzle for X.
% [X,steps] = sudoku(X) also returns the number of steps.
% See also sudoku_all, sudoku_assist, sudoku_basic, sudoku_puzzle. if nargin < 1X = sudoku_puzzle(1);endif nargin < 2steps = 0;gui_init(X);endsudoku_gui(X,steps);% Fill in all "singletons", the cells with only one candidate.% C is the array of candidates for each cell.% N is the vector of the number of candidates for each cell.% s is the index of the first cell with the fewest candidates.[C,N] = candidates(X);while all(N>0) & any(N==1)sudoku_gui(X,steps,C);s = find(N==1,1);X(s) = C{s};steps = steps + 1;sudoku_gui(X,steps,C);[C,N] = candidates(X);endsudoku_gui(X,steps,C);% Recursive backtracking.if all(N>0)Y = X;s = find(N==min(N),1);for t = [C{s}] % Iterate over the candidates.X = Y;sudoku_gui(X,steps,C);X(s) = t; % Insert a tentative value.steps = steps + 1;sudoku_gui(X,steps,C,s); % Color the tentative value.[X,steps] = sudoku(X,steps); % Recursive call.if all(X(:) > 0) % Found a solution.breakendsudoku_gui(X,steps,C,-s); % Revert color of tentative value.endendif nargin < 2gui_finish(X,steps);end% ------------------------------function [C,N] = candidates(X)% C = candidates(X) is a 9-by-9 cell array of vectors% C{i,j} is the vector of allowable values for X(i,j).% N is a row vector of the number of candidates for each cell.% N(k) = Inf for cells that already have values.tri = @(k) 3*ceil(k/3-1) + (1:3);C = cell(9,9);for j = 1:9for i = 1:9if X(i,j)==0z = 1:9;z(nonzeros(X(i,:))) = 0;z(nonzeros(X(:,j))) = 0;z(nonzeros(X(tri(i),tri(j)))) = 0;C{i,j} = nonzeros(z)';endendendN = cellfun(@length,C);N(X>0) = Inf;N = N(:)';end % candidates% ------------------------------function gui_init(X)% Initialize gui% H is the structure of handles, saved in figure userdata.dkblue = [0 0 2/3];dkgreen = [0 1/2 0];dkmagenta = [1/3 0 1/3];grey = [1/2 1/2 1/2];fsize = get(0,'defaulttextfontsize');fname = 'Lucida Sans Typewriter';clfshgset(gcf,'color','white')axis squareaxis offfor m = [2 3 5 6 8 9]line([m m]/11,[1 10]/11,'color',grey)line([1 10]/11,[m m]/11,'color',grey)endfor m = [1 4 7 10]line([m m]/11,[1 10]/11,'color',dkmagenta,'linewidth',4)line([1 10]/11,[m m]/11,'color',dkmagenta,'linewidth',4)endH.a = zeros(9,9);for j = 1:9for i = 1:9if X(i,j) > 0string = int2str(X(i,j));color = dkblue;elsestring = ' ';color = dkgreen;endH.a(i,j) = text((j+1/2)/11,(10.5-i)/11,string, ...'units','normal','fontsize',fsize+6,'fontweight','bold', ...'fontname',fname,'color',color,'horizont','center');endendstrings = {'step','slow','fast','finish'};H.b = zeros(1,4);for k = 1:4H.b(k) = uicontrol('style','toggle','string',strings{k}, ...'units','normal','position',[(k+3)*0.125,0.05,0.10,0.05], ...'background','white','value',0, ...'callback', ...'H=get(gcf,''user''); H.s=find(H.b==gco); set(gcf,''user'',H)');endset(H.b(1),'style','pushbutton')H.s = 1;H.t = title('0','fontweight','bold');set(gcf,'userdata',H)drawnowend % gui_init% ------------------------------function sudoku_gui(X,steps,C,z)H = get(gcf,'userdata');if H.s == 4if mod(steps,50) == 0set(H.t,'string',int2str(steps))drawnowendreturnelseset(H.t,'string',int2str(steps))endk = [1:H.s-1 H.s+1:4];set(H.b(k),'value',0);dkblue = [0 0 2/3];dkred = [2/3 0 0];dkgreen = [0 1/2 0];cyan = [0 2/3 2/3];fsize = get(0,'defaulttextfontsize');% Update entire array, except for initial entries.for j = 1:9for i = 1:9if ~isequal(get(H.a(i,j),'color'),dkblue) && ...~isequal(get(H.a(i,j),'color'),cyan)if X(i,j) > 0set(H.a(i,j),'string',int2str(X(i,j)),'fontsize',fsize+6, ...'color',dkgreen)elseif nargin < 3set(H.a(i,j),'string',' ')elseif length(C{i,j}) == 1set(H.a(i,j),'string',char3x3(C{i,j}),'fontsize',fsize-4, ...'color',dkred)elseset(H.a(i,j),'string',char3x3(C{i,j}),'fontsize',fsize-4, ...'color',dkgreen)endendendendif nargin == 4if z > 0set(H.a(z),'color',cyan)elseset(H.a(-z),'color',dkgreen)returnendend% Gui action = single step, brief pause, or no pauseswitch H.scase 1H.s = 0;set(gcf,'userdata',H);while H.s == 0;drawnowH = get(gcf,'userdata');endcase 2pause(0.5)case 3drawnowendif nargin == 4if z > 0set(H.a(z),'color',cyan)elseset(H.a(-z),'color',dkgreen)returnendend% ------------------------------function s = char3x3(c)% 3-by-3 character array of candidates.b = blanks(5);s = {b; b; b};for k = 1:length(c)d = c(k);p = ceil(d/3);q = 2*mod(d-1,3)+1;s{p}(q) = int2str(d);endendend % gui% ------------------------------function gui_finish(X,steps)H = get(gcf,'userdata');H.s = 2;set(H.b(1:3),'vis','off')set(gcf,'userdata',H)set(H.b(4),'string','close','value',0, ...'callback','close(gcf)')sudoku_gui(X,steps)end % gui_finishend % sudoku

备选项计算&数独题目生成:
%% Candidates备选项计算% C = candidates(X) 为向量数组构成的单元结构
% C{i,j} 为 X(i,j)构成的集合C = cell(9,9);tri = @(k) 3*ceil(k/3-1) + (1:3);for j = 1:9for i = 1:9if X(i,j)==0z = 1:9;z(nonzeros(X(i,:))) = 0;z(nonzeros(X(:,j))) = 0;z(nonzeros(X(tri(i),tri(j)))) = 0;C{i,j} = nonzeros(z)';endendendC%% First singleton and first empty. 第一个单选数,第一个空白网格% N = number of candidates in each cell.
% s = first cell with only one candidate.
% e = first cell with no candidates.N = cellfun(@length,C)s = find(X==0 & N==1,1)e = find(X==0 & N==0,1)%% Sudoku puzzles 数独题目生成help sudoku_puzzlefor p = 1:16sudoku_puzzle(p)end常微分方程
matlab提供了很多求给定常微分方程数组近似解的函数,这一常微分方程组数值解的函数包括ode23、ode45、ode113、ode23s、ode15s、ode23t、ode23tb。函数名中的数字表示所用算法的阶次,阶次和算法的复杂程度和精度有关。所有这些函数都会自动选择近似步长,来保证预先选择的精度要求。所选择的阶次越高,每一步计算量越大,但是所用的步长也越大。比如ode23算法比较二阶和三阶算法来估计计算步长,而ode45比较的是四阶和五阶算法。
s表示为stiff 刚性微分方程的求解函数。
微分方程求解程序库提供的求解函数都至少需要下面三个输入变元:
(1)F为定义微分方程组的函数
(2)tspan为描述积分区间的向量
(3) y0为初始值的向量
ode1的算法-误差较大
function [t,y] = ode1(F,tspan,y0) % ODE1 World's simplest ODE solver. % ODE1(F,[t0,tfinal],y0) uses Euler's method to solve % dy/dt = F(t,y) % with y(t0) = y0 on the interval t0 <= t <= tfinal.t0 = tspan(1); tfinal = tspan(end); h = (tfinal - t0)/200; y = y0; for t = t0:h:tfinalydot = F(t,y);y = y + h*ydot; end
用匿名函数生成微分方程:
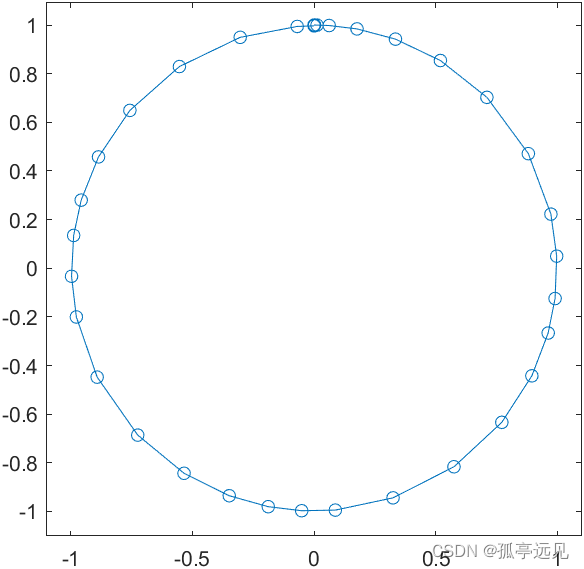
acircle = @(t,y) [y(2); -y(1)];ode23求解
%% ODE23 Automatic Plotting.figuretspan = [0 2*pi];y0 = [0; 1];ode23(acircle,tspan,y0)%% Phase Plot.figuretspan = [0 2*pi];y0 = [0; 1];[t,y] = ode23(acircle,tspan,y0)plot(y(:,1),y(:,2),'-o')axis squareaxis([-1.1 1.1 -1.1 1.1])%% ODE23 Automatic Phase Plot.opts = odeset('outputfcn',@odephas2)ode23(acircle,tspan,y0,opts)axis squareaxis([-1.1 1.1 -1.1 1.1])odeset