怎么给汽车网站做推广北京网络推广公司排行
基础解系的概念
线性方程组的解
21行列式和矩阵秩Rank的等价刻画
子式
标准型
利用子式求解矩阵的rank
24零积秩不等式
齐次线性方程组的基础解系
rank的两个重要结论
￥25伴随矩阵的rank
奇异矩阵：行列式=0的矩阵
31线性相关，线性无关，拓展与证明
n个m维向量在n<=m时可能线性相关也可能线性无关，线性无关时可以构成某个m维空间的一组基。m不小于n时，秩小于n则线性相关。
n个m维向量在n>m时可一定线性相关。低维向量一定无法构成高维度空间的一组基。
￥
32极大线性无关组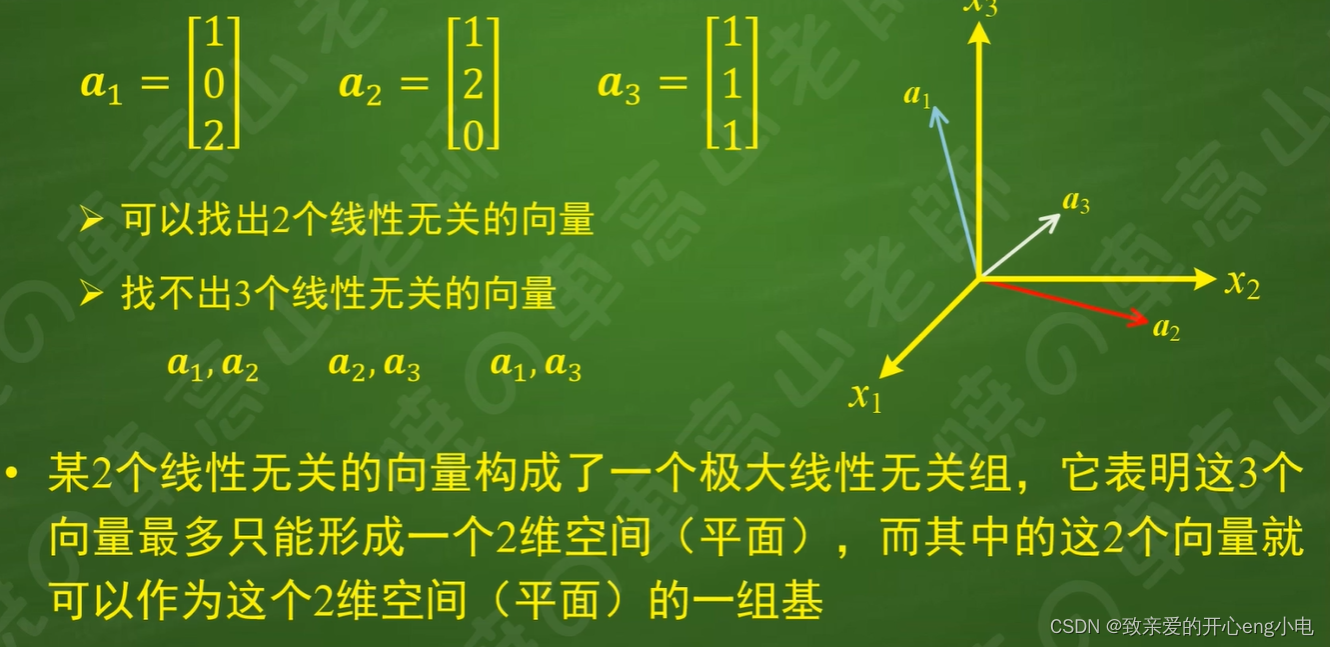
33向量组的等价
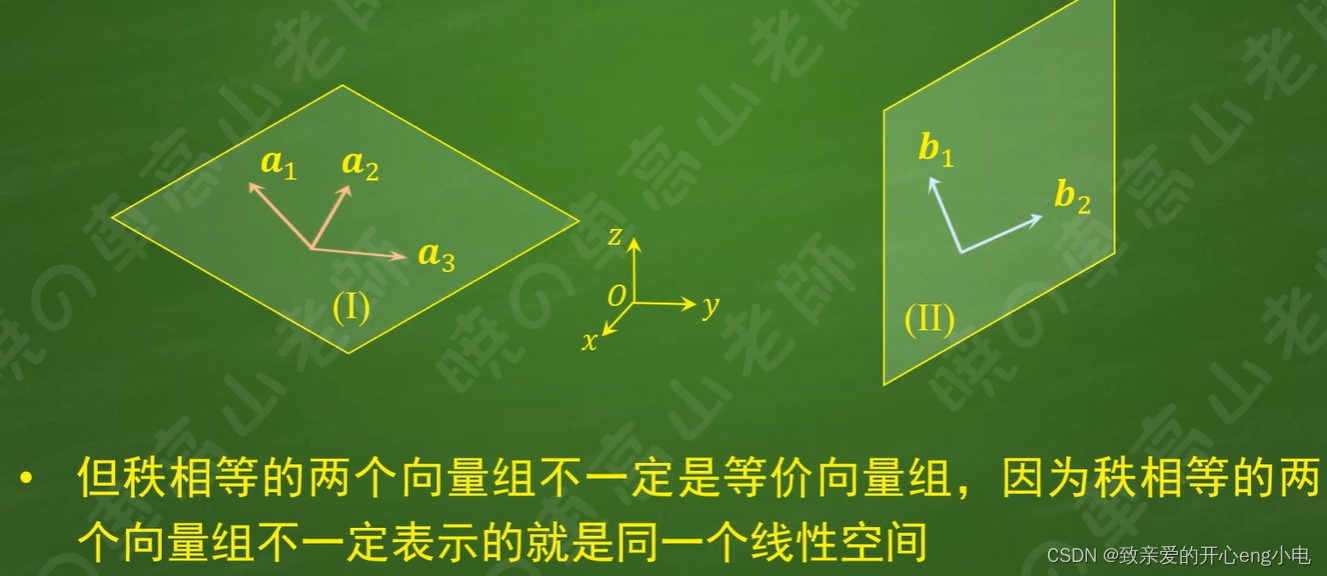
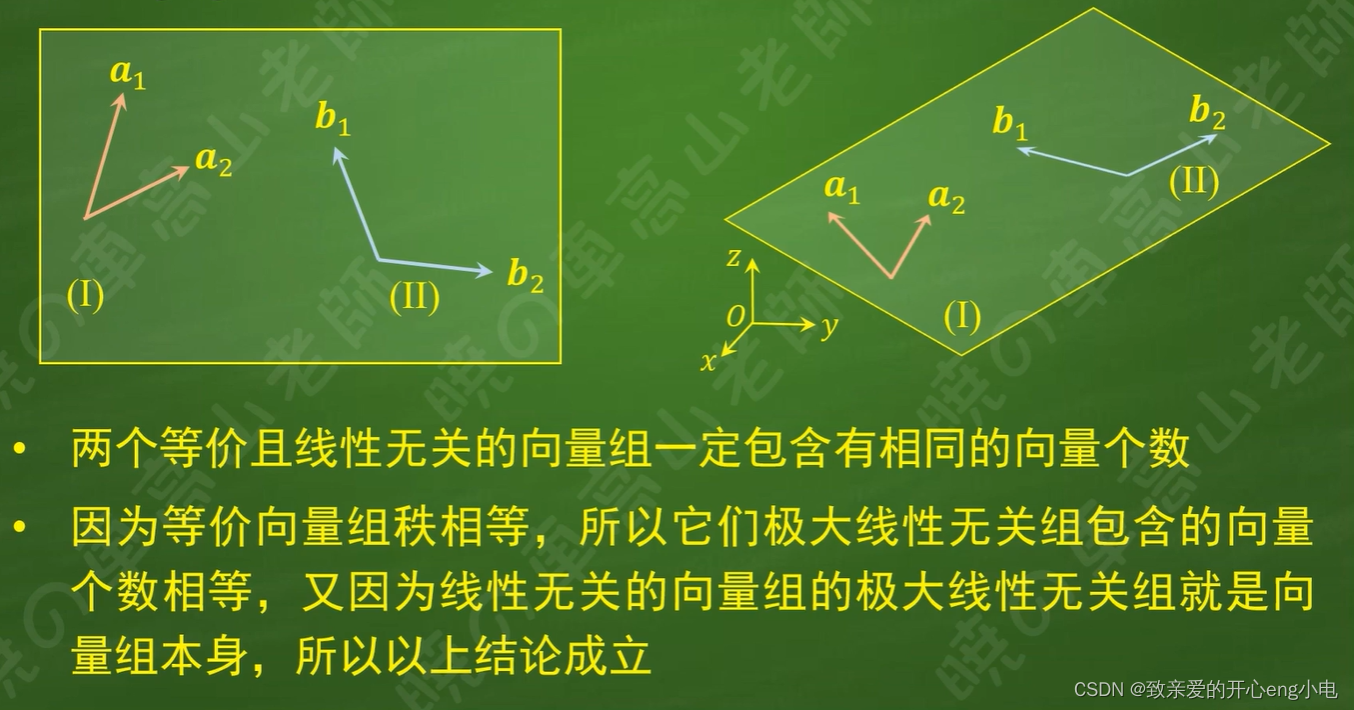
34线性空间基变换
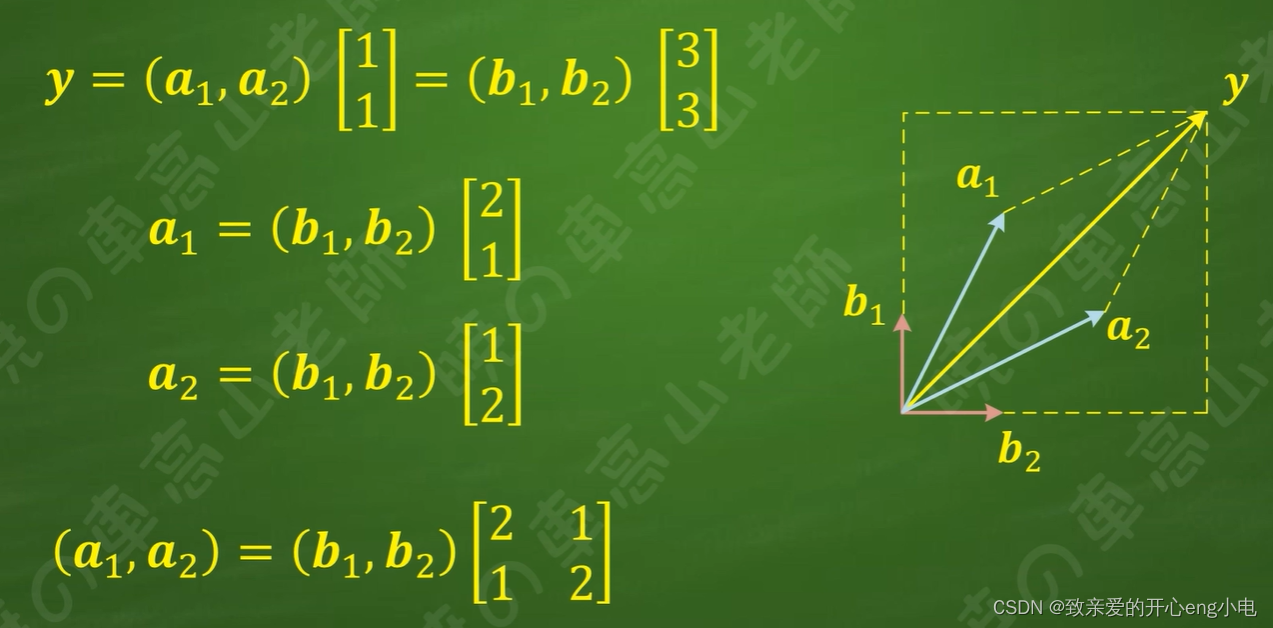
待研究的内容：
1线性无关向量的正交化
2矩阵的特征值和特征向量
3相似矩阵和相似对角化
4二次型及标准二次型
￥35单位正交基向量
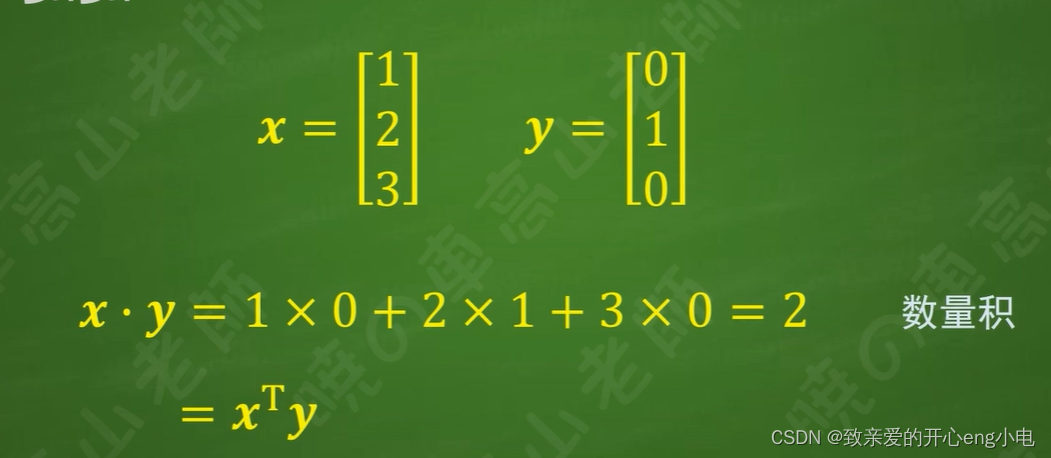两个向量的数量积等于0，则称两者正交或者垂直
研究它的原因：正交基向量，单位正交基向量有非常良好的性质
36斯密特正交化
37特征值和特征向量
概念篇
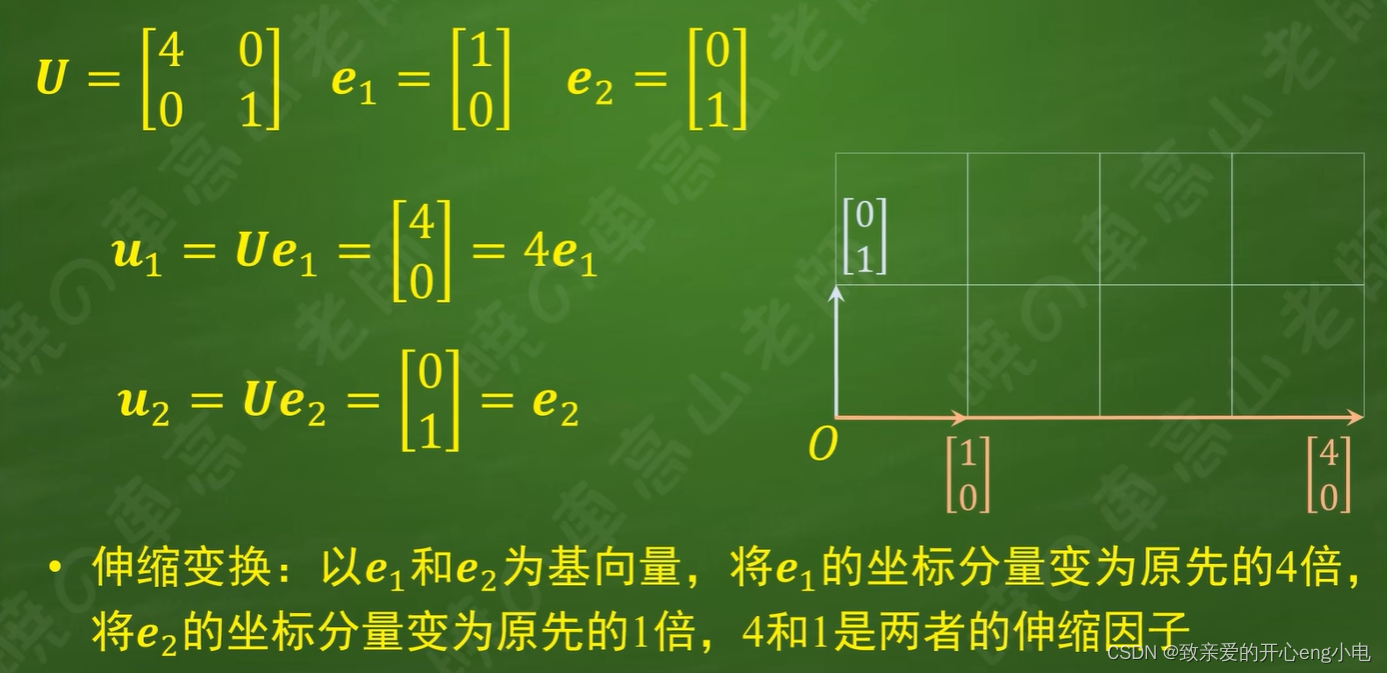
计算篇
性质篇
引用篇
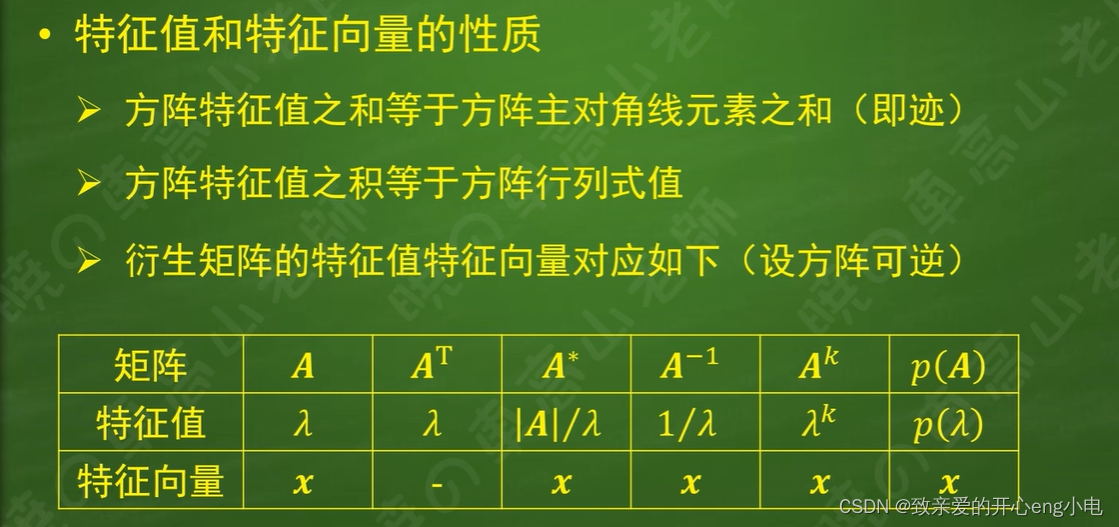
39特征值和特征向量的性质
40特征值和特征向量的计算例题
求特征值和特征向量的步骤
特征值和特征向量的关系
特征值和特征向量的性质
【补充】linear algebra and its applicationsCH4 vector spaces
4.1vector spaces and subspaces
4.2null spaces,column spaces, and linear transformation
4.3linear independent set:bases
4.4coordinate systems
4.5the dimension of a vector space
4.6rank
4.7change of basis
4.8applications to different equations
4.9applications to markov chains