常用网站域名青岛网站制作推广
一、图概述
定义:
图(graph)是由一些点(vertex)和这些点之间的连线(edge)所组成的;
其中,点通常被成为"顶点(vertex)“,而点与点之间的连线则被成为"边或弧”(edege)。
通常记为,G=(V,E)。
图是一种重要的数据结构,基本概念包括:顶点,边,有向,无向,权,路径回路,连通域,邻接点,度,入边,出边,入度,出度等等,很好理解。
参考这篇博客:http://www.cnblogs.com/skywang12345/p/3691463.html
二、图基础
2 图的分类
根据边是否有方向,将图可以划分为:无向图和有向图。
2.1.1 无向图
即两个顶点之间没有明确的指向关系,只有一条边相连,例如,A顶点和B顶点之间可以表示为 <A, B> 也可以表示为<B, A>,如下所示
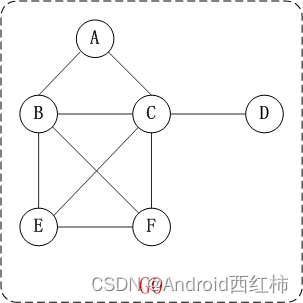
上面的图G0是无向图,无向图的所有的边都是不区分方向的。
我们用 **图 = (顶点集合,{边集合})**来表示图。
G0=(V1,{E1}) 其中,
(01) V1={A,B,C,D,E,F}。 V1表示由"A,B,C,D,E,F"几个顶点组成的集合。
(02) E1={(A,B),(A,C),(B,C),(B,E),(B,F),(C,F), (C,D),(E,F),(C,E)}。 E1是由边(A,B),边(A,C)…等等组成的集合。其中,(A,C)表示由顶点A和顶点C连接成的边。
2.2.2 有向图
顶点之间是有方向性的,例如A和B顶点之间,A指向了B,B也指向了A,两者是不同的,如果给边赋予权重,那么这种异同便更加显著了
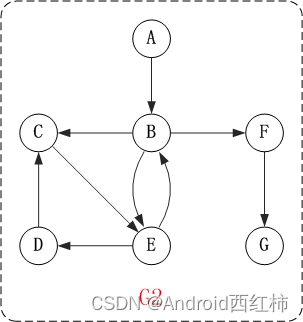
上面的图G2是有向图。
和无向图不同,有向图的所有的边都是有方向的!
3、邻接点和度
3.1 邻接点
一条边上的两个顶点叫做邻接点。
例如,上面无向图G0中的顶点A和顶点C就是邻接点。
在有向图中,除了邻接点之外;还有"入边"和"出边"的概念。
顶点的入边,是指以该顶点为终点的边。而顶点的出边,则是指以该顶点为起点的边。
例如,上面有向图G2中的B和E是邻接点;<B,E>是B的出边,还是E的入边。
3.2 度
在无向图中,某个顶点的度是邻接到该顶点的边(或弧)的数目。
例如,上面无向图G0中顶点A的度是2。
在有向图中,度还有"入度"和"出度"之分。
某个顶点的入度,是指以该顶点为终点的边的数目。
而顶点的出度,则是指以该顶点为起点的边的数目。顶点的度=入度+出度。
例如,上面有向图G2中,顶点B的入度是2,出度是3;顶点B的度=2+3=5。
4、路径和回路
路径:如果顶点(Vm)到顶点(Vn)之间存在一个顶点序列。则表示Vm到Vn是一条路径。
路径长度:路径中"边的数量"。
简单路径:若一条路径上顶点不重复出现,则是简单路径。
回路:若路径的第一个顶点和最后一个顶点相同,则是回路。
简单回路:第一个顶点和最后一个顶点相同,其它各顶点都不重复的回路则是简单回路。
三、图的存储结构
上面了解了"图的基本概念",下面开始介绍图的存储结构。图的存储结构,常用的是"邻接矩阵"和"邻接表"。
3.1 邻接矩阵
邻接矩阵是指用矩阵来表示图。它是采用矩阵来描述图中顶点之间的关系(及弧或边的权)。假设图中顶点数为n,则邻接矩阵定义为:

下面通过示意图来进行解释。
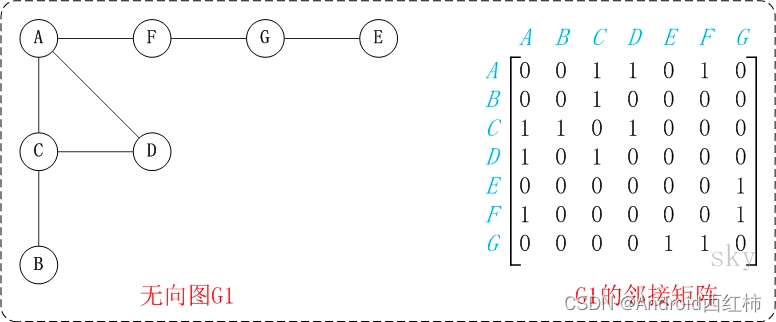
图中的G1是无向图和它对应的邻接矩阵。
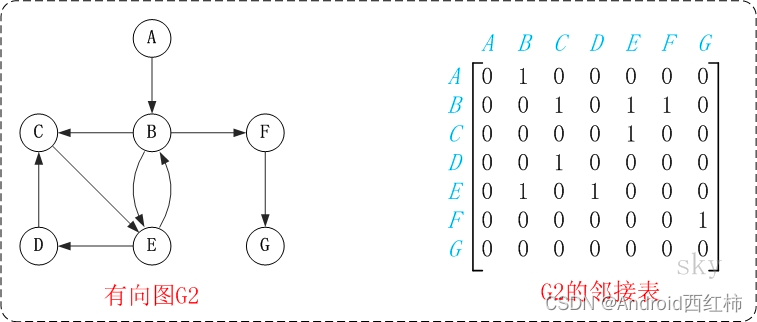
图中的G2是有向图和它对应的邻接矩阵。
通常采用两个数组来实现邻接矩阵:一个一维数组用来保存顶点信息,一个二维数组来用保存边的信息。
邻接矩阵的缺点就是比较耗费空间。
3.2 邻接表
邻接表是图的一种链式存储表示方法。它是改进后的"邻接矩阵",它的缺点是不方便判断两个顶点之间是否有边,但是相对邻接矩阵来说更省空间。

图中的G1是无向图和它对应的邻接矩阵。
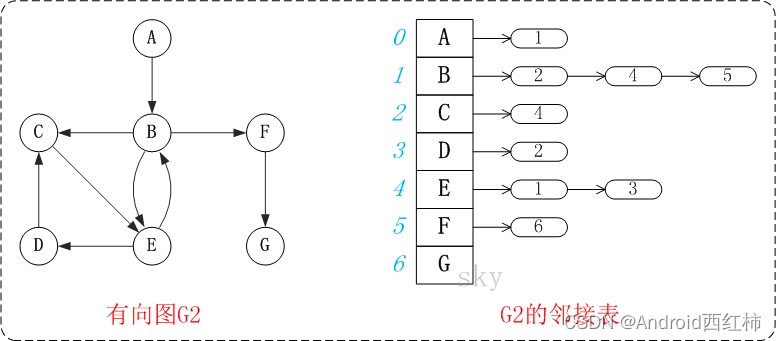
图中的G2是无向图和它对应的邻接矩阵。
3.3 十字链表
对于邻接表来说,计算顶点的入度是不方便的,那么有没有一种存储方式能够轻松的计算顶点的入度和出度呢,在十字链表中重新定义了节点的结构:
3.4 使用
实际使用,我们在拓扑排序中,使用邻接矩阵来实现,这是i个二维数组
首先,定义一些属性,用来存放节点数、顶点名称、排序后的顺序,图关系矩阵
/*** 节点个数*/public int size;/*** 顶点名称*/char [] nodeName;/*** 排序后的顺序*/List result;/*** 图关系矩阵*/int [][] matrix;
然后排序
// 排序public void tuopuSort() {System.out.println("\n");// 一个一维数组,用来保存顶点的入度int indegree[] = new int[size];boolean indegreeV[] = new boolean[size];// 给入度输入值for(int i = 0; i < size; i ++) {indegreeV[i] = false;for (int j = 0; j < size; j ++) {if (matrix[i][j] == 1) {indegree[j] = indegree[j] + 1;}}}System.out.println("\n");//开始进行遍历LinkedList<String> nodes = new LinkedList<String>();// 将入度为 0 的节点入队列for (int x = 0; x < size; x ++) {if (indegree[x] == 0) {System.out.println(nodeName[x]);nodes.add(String.valueOf(nodeName[x]));}}int j = 0;while (!nodes.isEmpty()) {for (int x = 0; x < size; x ++) {System.out.println("\n 数组 x = " + x + ", ");if (indegree[x] == 0 && !indegreeV[x]) {indegreeV[x] = true;String s = nodes.poll();System.out.println("add = " +s);result.add(s);// 找到跟它相关的节点,,入度 -1for (int y = 0; y < size; y ++) {if (matrix[x][y] == 1) {System.out.println("相关的节点 -1 = " + y);indegree[y] = indegree[y] - 1;if (indegree[y] == 0) {System.out.println("相关的节点 -1 后, 入度为0, " + nodeName[y]);nodes.add(String.valueOf(nodeName[y]));}}}} else {}}j ++;}System.out.println(result);}
四、图的遍历
深度优先遍历(DFS) & 广度优先遍历(BFS)
详细请看另外一篇文章
