网站权重提升工具河南百度seo
目录
1. 朴素解法
2. 优化
原题链接:
3. 完全背包问题 - AcWing题库
题目描述:
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i 种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行两个整数 vi, wi,用空格隔开,分别表示第 i 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0< N, V ≤10000
0< vi, wi ≤ 1000输入样例
4 5 1 2 2 4 3 4 4 5输出样例:
10
在解决这道题之前我们先来回顾一下 Acwing 的讲师:y总,他讲述的解决动态规划问题的一般步骤 。
集合:表示状态中每一个下标位置可能的选择。一维数组也好二维数组也罢,动态规划处理之后里面存储的元素就是这个状态下对应的最终结果。而这个结果的产生,就是集合中满足题意的那个元素。属性:属性需要根据题意来选择。就拿本题来说,要计算价值的最大值,那么属性就是集合中价值的最大值!
状态计算:将每一个状态中的集合进行划分,根据集合的划分推出状态转移方程。
集合划分的依据:划分出来的所有集合的并集不得遗漏一个状态中的任何选择。但是可以重复。
1. 朴素解法
这道题的状态表示和 01 背包问题里面的状态表示相同。
状态表示中的集合:从 1 - i 个物品中选,并且物品的总体积不超过 j 的所有选法!
状态表示中的属性:集合中所有选法的价值最大值。
我想,你现在对 集合 与 属性的关系一定有了自己的理解!动态规划存储结果的数组中的一个元素都是该状态下的集合中满足一定属性的那个值!
下面我们来看状态计算:我们在 01 背包问题中,将集合划分成了是否选择第 i 个物品两个部分。我们可以借鉴 01 背包问题的思路。
完全背包问题中,我们将集合划分为:
第 i 个物品选择 0 个,
第 i 个物品选择 1 个,
第 i 个物品选择 2 个,
······,
第 i 个物品选择 k 个
若干个部分。
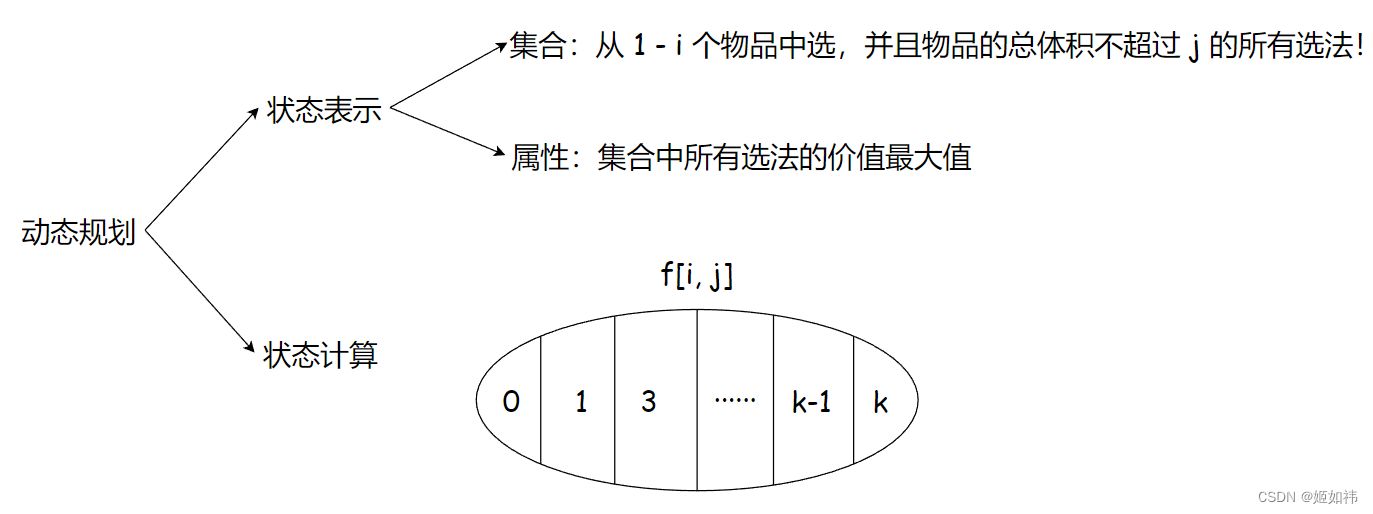
根据上图,我们将集合划分成了若干部分,并且如此划分集合满足集合划分的依据,下一步要做的就是推导出状态转移方程,即如何计算出集合中价值的最大值。
同时我们还注意到: k 不能胡乱取值,因为我们的背包体积是有限的,当 k * v[i] 大于 背包的体积,此时往后的 k 都是无效的。
下面我们来推导状态转移方程:
我们不妨假设第 i 个物品我们选择了 k 个。
当 k = 0 时,说明不选择第 i 个物品,此时 f [i, j] = f [i - 1, j],这倒是很简单!
当 k 不等于 0 时该怎么办呢?同样借鉴一下 01 背包问题的想法:之前假设第 i 个物品选择了 k 个,我们可以先不看第 i 个物品,那么问题就变成了从 1 - (i - 1) 中的物品中做选择,但是选择的体积还是不大于 j 吗?当然不是,因为我们忽略了第 i 个物品,并且我们选择了 k 个第 i 个物品,因此选择的总体积应该是不大于 j - k * v[i],(v[i] 是第 i 个物品的体积)。
那么当 k 不等于 0 时,状态转移方程就可以写成:f [i, j] = f [ i - 1][ j - k * v[i] ] + k * w[i]。这里为什么要加上 k * w[i] 呢?因为 f [ i - 1][ j - k * v[i] ] 是忽略了第 i 个物品的选择的价值最大值,想要计算 f [ i, j ] 肯定要算上第 i 个物品的选择嘛!
最后我们惊奇的发现,k = 0 与 k != 0,f [i, j] 都等于 f [ i - 1][ j - k * v[i] ] + k * w[i]。
因为要求的是价值的最大值,因此在遍历 k 的取值时要取价值最大的那一个!
#include<iostream>
#include<algorithm>
using namespace std;const int N = 1010;
int v[N], w[N];
int f[N][N];
int n, m;int main()
{cin >> n >> m;for(int i = 1; i <= n; i++)cin >> v[i] >> w[i];for(int i = 1; i <= n; i++){for(int j = 0; j <= m; j++){for(int k = 0; k * v[i] <= j; k++){f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);}}}cout << f[n][m] << endl;return 0;
}2. 优化
优化的味道有点向数学,我们需要将 f[i, j] 的状态转移方程展开:
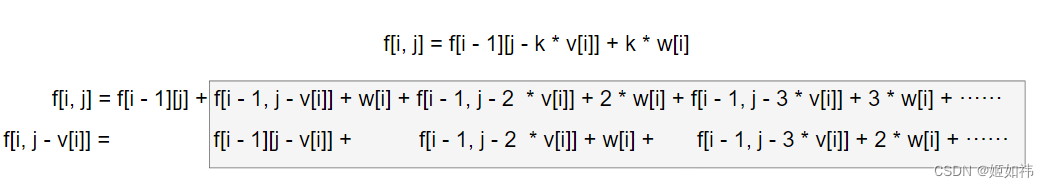
我们发现灰色的那一坨是差不多的,就差了一个 w[i],因此我们的状态转移方程可以修改为:
f[i, j] = max( f[i - 1][j] + f[i, j - v[i]] + w[i] )
#include<iostream>
#include<algorithm>
using namespace std;const int N = 1010;
int v[N], w[N];
int f[N][N];
int n, m;int main()
{cin >> n >> m;for(int i = 1; i <= n; i++)cin >> v[i] >> w[i];for(int i = 1; i <= n; i++){for(int j = 0; j <= m; j++){f[i][j] = f[i - 1][j];if(j >= v[i])f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);}}cout << f[n][m] << endl;return 0;
}再根据 01 背包问题的空间优化,完全背包问题的空间也是可以优化到一维的,并且根据状态转移方程,从小到大枚举并无问题,因为 j - v[i] 一定在之前被计算过,因此,完全背包问题的最终代码:
#include<iostream>
#include<algorithm>
using namespace std;const int N = 1010;
int v[N], w[N];
int f[N];
int n, m;int main()
{cin >> n >> m;for(int i = 1; i <= n; i++)cin >> v[i] >> w[i];for(int i = 1; i <= n; i++)for(int j = v[i]; j <= m; j++)f[j] = max(f[j], f[j - v[i]] + w[i]);cout << f[m] << endl;return 0;
}