做logo用什么网站seo线下培训课程

在探究三维空间下的变换前，首先研究二位空间，因为比较直观，再推广到三维空间。
首先应该清楚的一点是：旋转、平移对于坐标系下的点以及坐标系本身而言都是相对的（运动的相对性）。

例如：

1. $XOY$坐标系不动，点$P(x,y)$沿顺时针方向旋转 $\theta$，得到点$P^{\prime }$，此时点$P^{\prime }$在$XOY$坐标系的坐标为$(x^{\prime },y^{\prime })$；
2. 点$P(x,y)$不动，坐标轴$XOY$沿着逆时针方向旋转 $\theta$，得到坐标轴$X^{\prime }O{Y}^{\prime }$，此时点$P$在$X^{\prime }O{Y}^{\prime }$下的坐标为$(x^{\prime },y^{\prime })$。
   这两条命题是等价的。

因此，仅讨论坐标系变换。

二维空间下的坐标系变换

平移：

旋转：

注：图片来源https://www.cnblogs.com/meteoric_cry/p/7987548.html




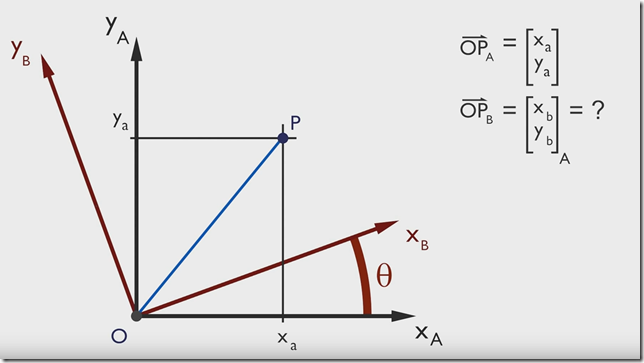
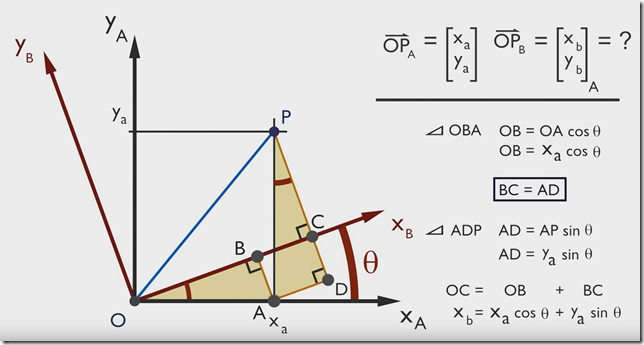
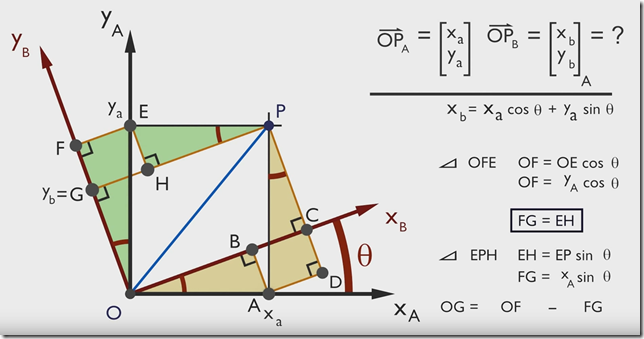
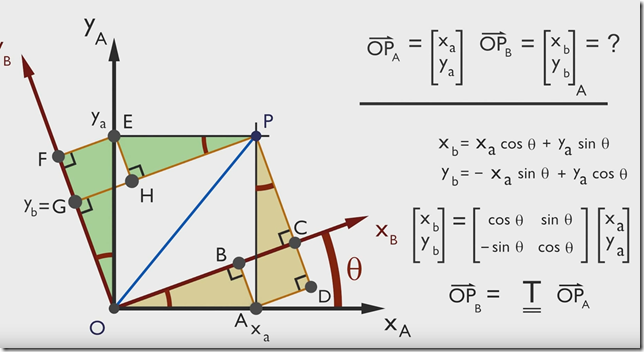
所以对于二维旋转来讲，旋转可描述为：设点$P$在$XOY$坐标系下坐标为$\left[\begin{array}{c}x\\ y\end{array}\right]$，将坐标系$XOY$顺时针旋转$\theta$后，$P$点坐标为$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]$，则有：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$
旋转矩阵可记为：$Q=\left[\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]$

三维空间下的坐标系变换

平移：

旋转：

三维空间下，当固定轴选定后，旋转就等价于：其余两轴在其平面内的（二维）旋转。
假设以逆着固定轴正向的方向看去的顺时针为旋转的正向。

1. 绕$x$轴旋转$\alpha$（在$yz$平面顺时针旋转）:
   
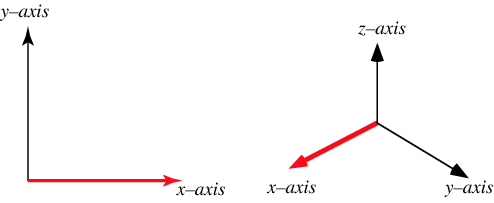
   则旋转前后的坐标变化可描述为：
   $$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ x^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cos\alpha & -sin\alpha & 0\\ 0& sin\alpha & cos\alpha & 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ x\\ 1\end{array}\right]$$

2. 绕$y$轴旋转$\beta$（在$xz$平面顺时针旋转）:
   
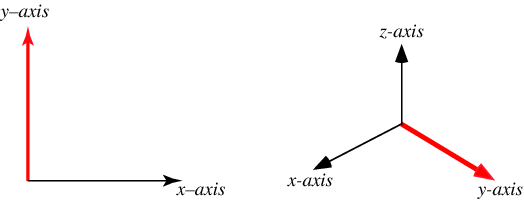
   则旋转前后的坐标变化可描述为：
   $$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ x^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}cos\beta & 0& sin\beta & 0\\ 0& 1& 0& 0\\ -sin\beta & 0& cos\beta & 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ x\\ 1\end{array}\right]$$

3. 绕$z$轴旋转$\gamma$（在$xy$平面顺时针旋转）:
   
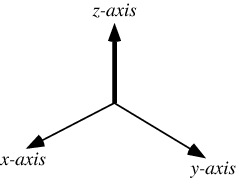
   则旋转前后的坐标变化可描述为：
   $$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ x^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}cos\gamma & -sin\gamma & 0& 0\\ sin\gamma & cos\gamma & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ x\\ 1\end{array}\right]$$

综上，当坐标系沿着$X,Y,Z$轴分别旋转$\alpha ,\beta ,\gamma$后，旋转矩阵为3个沿单一坐标轴旋转的旋转矩阵的乘积，前后的坐标变化可描述为：

Reference：

1. 旋转矩阵（Rotation Matrix）的推导及其应用
2. Wolfram MathWorld: Rotation Matrix
3. 3d变换基础：平移、旋转、缩放（仿射变换）详解——公式推导