天河区网站制作百度搜索入口官网
- 约瑟夫问题重述:
在计算机编程的算法中,类似问题又称为约瑟夫环
约瑟夫环:N个人围成一圈,从第一个开始报数,第M个将被杀掉,最后剩下一个,其余人都将被杀掉。
例如N=6,M=5,被杀掉的顺序是:5,4,6,2,3,1。
如图所示
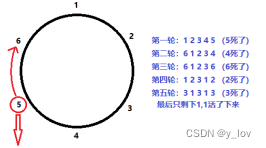
2.约瑟夫问题递归法计算原理:
2.1 内容:设F(N,M)为最后存活者的位置(位置从0开始),则有:
F(N,M)=(F(N-1,M)+M)%N
2.2 证明:数学归纳法
· 当n=1时,f(1,m)=0,因为编号从0开始且只有一个人,胜利者编号显然为0。 当n=2时,序列为0,1,若m为奇数,则胜利者编号为1;若m为偶数,则胜利者编号为0,易有f(2,m)=m%2=(0+m)%2=[f(1,m)+m]%2,结论成立。
· 假设当n=i-1时结论成立,即对于序列0,1,2,...,i-2而言,最后的胜利者编号为f(i-1,m)。 当n=i时,序列为0,1,2,...,i-1。设第一轮的淘汰者编号为k(若m%i=0,则k=i-1,否则k=m%i-1),则序列可表示为0,1,2,...,k-1,k,k+1,...,i-1。第一轮淘汰k,余下的序列x'为k+1,...,i-1,0,1,...,k-1,问题规模变为i-1。 因为由归纳假设,当n=i-1时,对于序列x:0,1,2,...,f(i-1,m),...,i-2,胜利者编号为f(i-1,m)。
由于x'=(x+k+1)%i,故f(i,m)=[f(i-1,m)+k+1]%i。当m%i=0时,k+1=i,[f(i-1,m)+k+1]%i=[f(i-1,m)+i]%i=f(i-1,m)%i+0=f(i-1,m)%i+m%i=[f(i-1,m)+m]%i;当m%i!=0时,k+1=m%i,[f(i-1,m)+k+1]%i=[f(i-1,m)+m%i]%i=[f(i-1,m)+m]%i。故当n=i时,结论成立。
· 综上,命题成立。
3.设计对象问题:
3.1问题重述:
假设你正在游玩约瑟夫游戏,从你开始报数,游戏规则与课上讲述一致,现在你想确保你是最后一个出列的玩家,如果由你设置m(即每报几个数出列一人),你应该如何设置m来确保自己的胜利?
3.2问题分析:
- F(N,M)=(F(N-1,M)+M)%N
- 设“我”的编号为S,总人数为N,每次第M个人被杀掉,S,N为已知量,M是待确定量;
- 最终目标:在保证F(N,M)+ S = S的条件下,确定M;
- 在确保时间复杂度,计算的开销等因素下,尽量进行优化的选取。
3.3问题求解:
F(N , M) = (F(N-1,M)+M) mod N (1)
F(N , M) = 0; ( 2 )
思路1:枚举法
1.实现:枚举m,运用公式计算F(N,M) , 找到满足条件的m;
2.复杂度:O(n*m);
3.优点: 思路简单,枚举足够多就能找到全部解,且容易。
4.缺点:用while()枚举,当大到一定程度终结。无法确定是否能找到m,以及m要枚举多大。
思路2:设计法
- 实现:
F(1,M) = 0;
F(2,M) = (M)%2 = 0;
F(3,M) = (M%2 +M)%3 = 0 ;
...
F(N,M) = (M%2 + M%3 + M%4 +...+M%N)%N = 0;
令 M = N!,则满足条件。
2.复杂度:O(N);
3.优点: 复杂度低
4.缺点:当N过大时,m数据值过大。
6.优化
1.操作:
双指针删因子法缩小m规模。
试图在不改变复杂度条件下删除公共因子以减小m的数据规模。
- 复杂度: O(N);
- 缺陷:降低规模效果不明显,依旧只能处理小范围数据
- 进一步优化:
- 方法1:用string进行大数计算;
- 方法2:用Python;
- 方法3:n小则用法2,n大用法1,但是依旧具有m不确定是否能找到的不稳定性。
只需在原有基础上修改为大数模式,在此除了方法三外不做具体实现。
