电子商务网站建设大作业昆明seo博客
337. 打家劫舍 III - 力扣(LeetCode)
一、题目
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
示例 1:
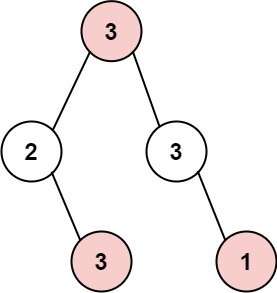
输入: root = [3,2,3,null,3,null,1] 输出: 7 解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
示例 2:
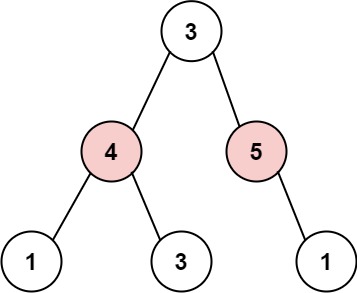
输入: root = [3,4,5,1,3,null,1] 输出: 9 解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9
提示:
- 树的节点数在
[1, 104]范围内 0 <= Node.val <= 104
二、代码
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public class Info {// 如果要抢劫当前节点的情况下,以当前节点为根节点的整棵树能获得的最大收益是多少public int yes;// 如果不抢劫当前节点的情况下,以当前节点为根节点的整棵树能获得的最大收益是多少public int no;public Info(int y, int n) {yes = y;no = n;}}public int rob(TreeNode root) {// 获取根节点root的Info信息Info ans = process(root);// 两种情况取最大值就是答案return Math.max(ans.no, ans.yes);}public Info process(TreeNode node) {// node节点左子树的信息Info leftInfo = null;// node节点右子树的信息Info rightInfo = null;// 递归手机左右子树的Infoif (node.left != null) {leftInfo = process(node.left);}if (node.right != null) {rightInfo = process(node.right);}// 左子树和右子树不抢根节点情况下整棵树的最大收益int leftNo = 0;int rightNo = 0;// 左子树和右子树抢根节点情况下整棵树的最大收益int leftYes = 0;int rightYes = 0;// 给上面四个变量赋值,如果没有左右子树了,相关的信息就默认为0if (leftInfo != null) {leftNo = leftInfo.no;leftYes = leftInfo.yes;}if (rightInfo != null) {rightNo = rightInfo.no;rightYes = rightInfo.yes;}// 情况一:抢劫node节点的情况下,计算以node节点为根节点的整颗树的最大收益// 这种情况下左右子节点都是不能抢劫的,否则会出发警报。所以这个的答案就是leftNo + rightNo + node.valint yes = leftNo + rightNo + node.val; // 要记得加上node节点本身的价值,因为这种情况还要抢劫node节点// 情况二:不抢劫node节点的情况下,计算以node节点为根节点的整颗树的最大收益// 这种情况下左右子树抢劫也可以,不抢也可以,都不会触发警报,因为没有同时抢劫直接相连的屋子// 所以这个就是取左子树抢劫和不抢劫两种情况的最大收益的最大值 + 右子树抢劫和不抢劫两种情况的最大收益的最大值 这个就是node节点情况二的最大收益int no = Math.max(leftNo, leftYes) + Math.max(rightNo, rightYes);// 返回node节点的Info信息return new Info(yes, no);}
}三、解题思路
如果两家直接相连的屋子被抢劫,会引发报警。一个节点和另外一点是父子关系就是挨着。
两种情况
- 在x屋子被抢了的情况下,以x为根节点的整棵树获得的最大收益
- 在x屋子不被抢的情况下,以x为根节点的整棵树获得的最大收益
情况一:
如果x屋子要抢的话,那么它的两个左右子节点都不可以抢。
这种情况以x为根的树能做到的最大收益就是左右两个子节点不被抢的最大收益加和 + x节点的val。
情况二:
如果x屋子不抢的话,那么它的两个左右子节点可以抢,也可以不抢。
这种情况以x为根的树能做到的最大收益就是取左孩子的抢和不抢这两种情况的最大收益中的最大值,再取右孩子的抢和不抢这两种情况的最大收益中的最大值,将这两个最大值相加就是x屋子不抢的最大收益值。
