找一家秦皇岛市做网站的公司商丘网站seo

(十一) 常用数据结构

学习数据结构：①模型 ②API ③实现、时间复杂度 ④应用

基础：动态数组、链表

其他数据结构：栈、队列、哈希表、位图、二叉树

算法：排序、二分查找

1.动态数组

(1)模型

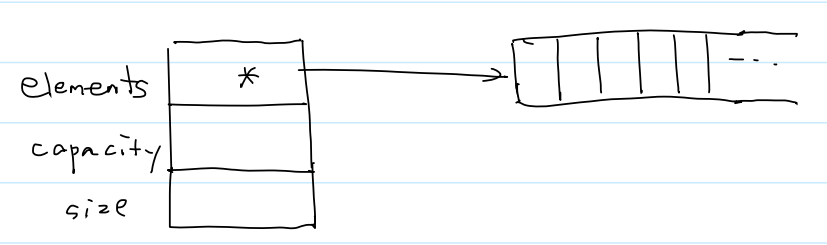
(2).h与.c

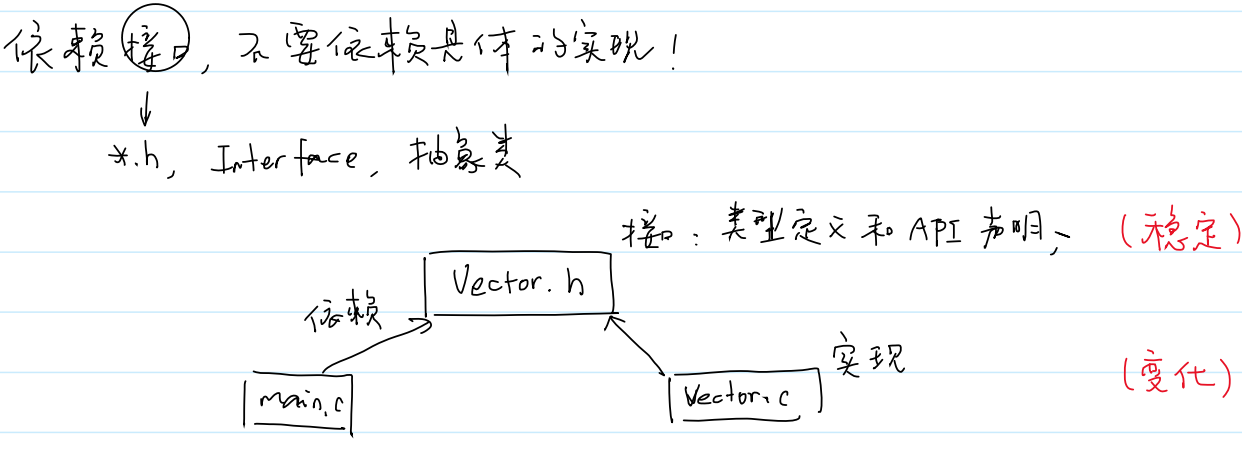
(3)实现

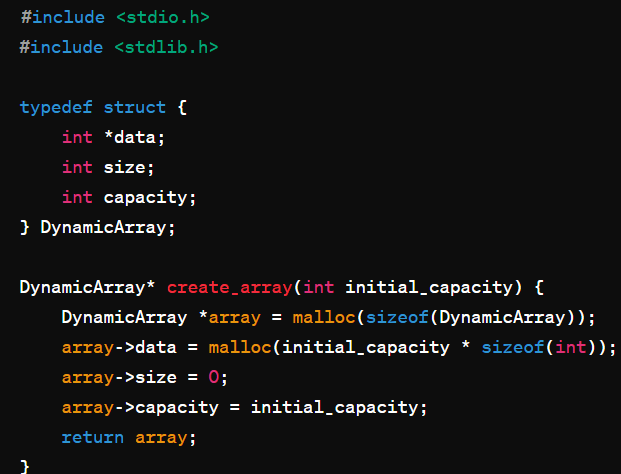
2.链表

(1)模型

1.单链表

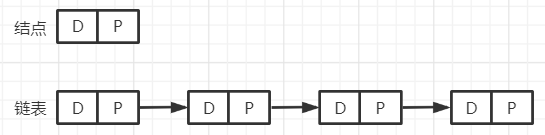
2.双链表

(2)分类

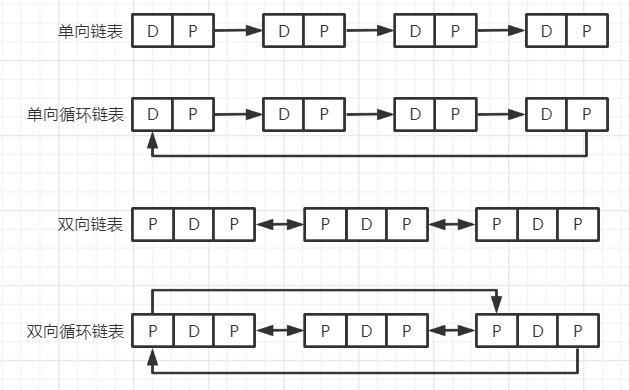
(3)基本操作(API)

1.单链表的基本操作
(1)增加：已知某个结点的指针，在该结点的后面添加新结点：时间复杂度O(1)
(2)删除：已知某个结点的指针，删除该结点后面的结点：时间复杂度O(1)
(3)查找：
①按位查找，根据索引查找结点，时间复杂度O(n)
②按值查找，查找与特定值相等的结点：元素大小无序、元素大小有序，都是O(n)

2.双链表的基本操作
(1)增加
(2)删除
(3)查找
①根据索引查找值
②查找与特定值相等的结点
③查找前驱结点
(4)遍历
①正向遍历
②逆向遍历

(4)实现

(1)结点、单链表定义

typedef struct node{  //结点int data;struct node* next;
} Node;typedef struct  {   //单链表Node* head;Node* tail;int size;
} List;

(2)析构函数

void node_destroy(Node* head) {Node* cur = head;while (cur != NULL) {Node* next = cur->next;free(cur);cur = next;}
}

(5)链表常见面试题

思路1：先遍历一遍，得到链表长度。再遍历第二次，找到中间节点。
时间O(n)，空间O(1)

思路2：快慢指针，fast一次走两步，slow一次走一步
时间O(n)，空间O(1)

fast == NULL || fast->next == NULL  //判断fast到达末尾，短路原则

思路1：
用数组保存已遍历过的结点指针
时间：遍历O(n)×查找效率
查找效率：哈希表O(1)，链表O(n)

思路2：快慢指针
如果无环，则fast先一定先到终点(变为NULL)，slow到中点
如果有环，fast与slow一定会在环中相遇
时间O(n)

思路1：头插法

思路2：递归
边界条件：head == NULL || head->next == NULL
递归公式：每次只反转第一个结点，假设后n-1个已经反转好了(实际并没有)
时间O(n)，空间O(n)，栈的深度

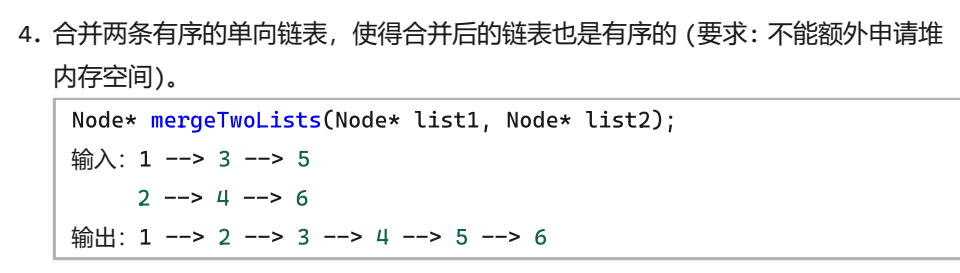
dummy node：哑结点(虚拟头结点，不存数据，仅为了方便结点的插入)

(6)空间与时间

①空间换时间：缓存、缓冲
②时间换空间：压缩、交换区(对换区)

3.栈

(1)模型

栈是操作受限的线性表，只能在同一端添加和删除元素。
能添加的一端称为栈顶(top)，不能添加删除的一端称为栈底(bottom)。
特性：FILO，LIFO

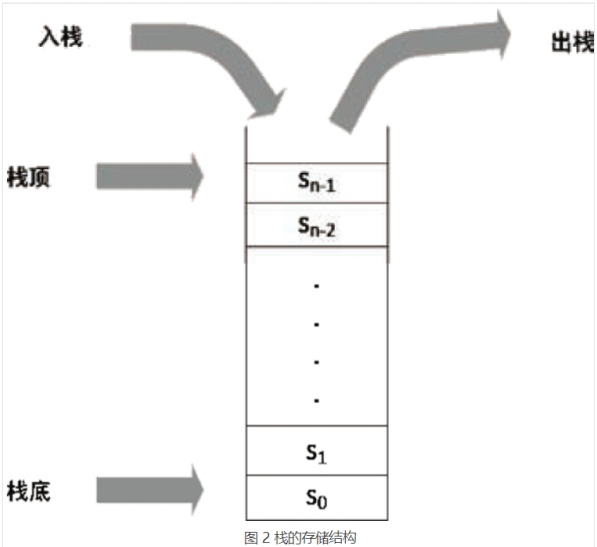
Q：为什么需要栈这种数据结构？数组和链表这种线性表不是都能实现吗？
A：①安全 ②可读性强 ③和现实生活中的场景有对应

(2)基本操作

①添加：入栈 Push
②删除：出栈 Pop
③查找：查栈顶 Peek
④判空：Empty

(3)实现

用链表实现链栈
(1)构造函数

Stack* stack_create(void) {return calloc(1, sizeof(Stack));
}

(2)析构函数

void stack_destroy(Stack* s) {Node* curr = s->top;while (curr != NULL) {Node* next = curr->next;free(curr);curr = next;}free(s);
}

(3)入栈

void stack_push(Stack* s, E val) {Node* push = calloc(1,sizeof(Node));if (push == NULL) {printf("Error: push failed because calloc failed.\n");exit(1);}push->next = s->top;push->data = val;s->top= push;s->size++;
}

(4)出栈

E stack_pop(Stack* s) {if (stack_empty(s)) {printf("Error: stack is empty, pop failed.\n");exit(1);}Node* remove = s->top;s->top = s->top->next;int ret_value = remove->data;free(remove);s->size--;return ret_value;
}

(5)查找栈顶元素

E stack_peek(Stack* s) {if (stack_empty(s)) {printf("Error: peek failed because the stack is empty.\n");exit(1);}return s->top->data;
}

(6)判空

bool stack_empty(Stack* s) {return s->size == 0;
}

(7)完整代码
//stack.h

#include <stdbool.h>
typedef int E;typedef struct node {E data;struct node* next;
} Node;typedef struct {Node* top;int size;
} Stack;// API
Stack* stack_create(void);
void stack_destroy(Stack* s);void stack_push(Stack* s, E val);
E stack_pop(Stack* s);
E stack_peek(Stack* s);bool stack_empty(Stack* s);

//stack.c

#include "stack.h"
#include <stdlib.h>
#include <stdio.h>Stack* stack_create(void) {return calloc(1, sizeof(Stack));
}void stack_destroy(Stack* s) {Node* curr = s->top;while (curr != NULL) {Node* next = curr->next;free(curr);curr = next;}free(s);
}void stack_push(Stack* s, E val) {Node* push = calloc(1,sizeof(Node));if (push == NULL) {printf("Error: push failed because calloc failed.\n");exit(1);}push->next = s->top;push->data = val;s->top= push;s->size++;
}E stack_pop(Stack* s) {if (stack_empty(s)) {printf("Error: stack is empty, pop failed.\n");exit(1);}Node* remove = s->top;s->top = s->top->next;int ret_value = remove->data;free(remove);s->size--;return ret_value;
}E stack_peek(Stack* s) {if (stack_empty(s)) {printf("Error: peek failed because the stack is empty.\n");exit(1);}return s->top->data;
}bool stack_empty(Stack* s) {return s->size == 0;
}

//main.c

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include "stack.h"
#include <stdio.h>int main(void) {Stack* s = stack_create();stack_push(s,1);stack_push(s,2);stack_push(s,3);stack_push(s,4);stack_destroy(s);return 0;
}

(4)栈的应用

特性：后进先出 LIFO
(1)函数调用栈
(2)符号匹配问题
(3)用单调栈表示优先级：表达式求值
(4)用栈来记录轨迹：
①递归
②网页的前进后退(前进栈、后退栈)
③深度优先搜索(DFS)
④回溯算法
⑤树的前中后序遍历
(5)进制转换

4.队列

(1)模型

队列是操作受限的线性表，一端添加元素，另一端删除元素
队尾(rear)添加元素，队头(front)删除元素
特性：FIFO，先进先出 (公平)

(2)基本操作(API)

①添加：入队列(queue_push)
②删除：出队列(queue_pop)
③查找：查看队头元素(queue_peek)
④判空：queue_empty
⑤判满：queue_full

(3)实现

(1)循环数组：用动态数组实现 顺序队列
(2)链表

a.只用rear标识队尾。缺点：出队 O(n)
b.front标识队头，rear标识队尾。缺点：极大浪费内存空间，否则需要大量移动元素
c.“循环”数组，实现循环队列。缺点：判空判满时都是 rear == front
d.①牺牲一个存储单元，有一个空间不存元素，认为已满，(rear+1)%capacity == front ②添加属性size，判空size == 0，判满size == capacity

if(rear == capacity){grow_capacity();
}
elements[rear] = val;
rear = (rear + 1)%capacity;

(1)构造函数

Queue* queue_create() {Queue* queue = calloc(1, sizeof(Queue));queue->elements = calloc(DEFAULT_SIZE, sizeof(E));queue->capacity = DEFAULT_SIZE;return queue;
}

(2)析构函数

void queue_destroy(Queue* q) {free(q->elements); //释放的是手动malloc的内容free(q);
}

(3)入队

void queue_push(Queue* q, E val) {if (q->size == q->capacity) {grow_capacity(q); //自动扩容}q->elements[q->rear] = val;q->rear = (q->rear + 1) % q->capacity;q->size++;
}

(4)自动扩容

//自动扩容
void grow_capacity(Queue* q) {if (q->size >= MAX_SIZE) {printf("Error: push failed, because queue size has reached MAX_SIZE.\n");printf("size = %d, capacity = %d, MAX_SIZE = %d\n", q->size, q->capacity, MAX_SIZE);exit(-1);}int new_capacity = (q->capacity << 1) < MAX_SIZE ? (q->capacity << 1) : MAX_SIZE;E* new_arr = calloc(new_capacity, sizeof(E));if (!new_arr) {printf("calloc failed of new_arr in grow_capacity.\n");exit(-1);}for (int i = 0; i < q->size; i++) {new_arr[i] = q->elements[q->front];q->front = (q->front + 1) % q->capacity;}E* temp = q->elements;free(temp);q->elements = new_arr;q->front = 0;q->rear = q->size;  //下一个要插入元素的位置，目前为空q->capacity = new_capacity;
}

自动扩容原理

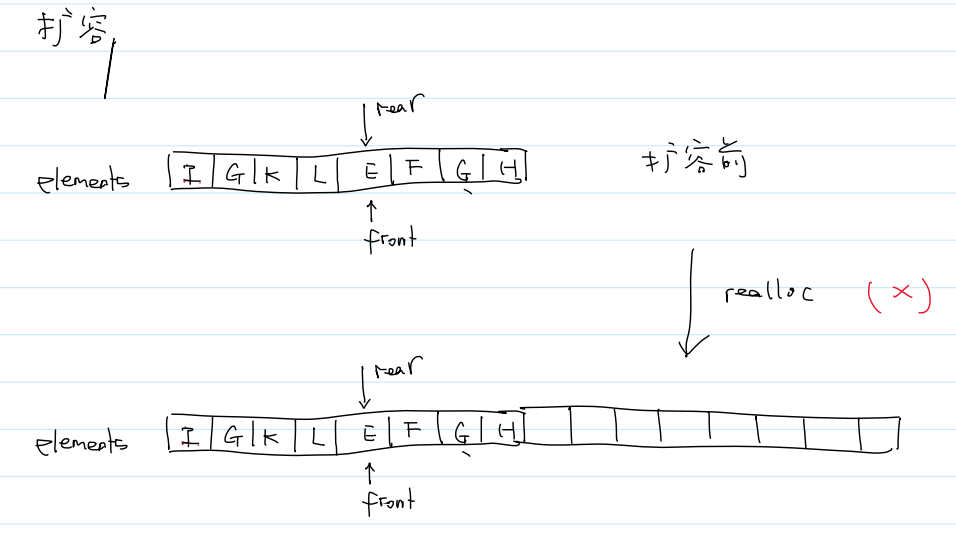
(5)出队

E queue_pop(Queue* q) {if (queue_empty(q)) {printf("Error: pop failed, because queue is empty.\n");exit(-1);}int ret_val = q->elements[q->front];q->front = (q->front + 1) % q->capacity;q->size--;return ret_val;
}

(6)查找队头元素

E queue_peek(Queue* q) {if (queue_empty(q)) {printf("Error: peek failed, because queue is empty.\n");exit(-1);}return q->elements[q->front];
}

(7)队列判空

bool queue_empty(Queue* q) {return q->size == 0;
}

(8)完整代码
//queue.h

#include <stdbool.h>typedef int E;typedef struct {E* elements;int front;int rear;int size;     //实际大小int capacity; //容量
} Queue;// API
Queue* queue_create();
void queue_destroy(Queue* q);void queue_push(Queue* q, E val);
E queue_pop(Queue* q);
E queue_peek(Queue* q);bool queue_empty(Queue* q);

//queue.c

#include "queue.h"
#include <stdlib.h>
#include <stdio.h>
#define MAX_SIZE 100
#define DEFAULT_SIZE 10Queue* queue_create() {Queue* queue = calloc(1, sizeof(Queue));queue->elements = calloc(DEFAULT_SIZE, sizeof(E));queue->capacity = DEFAULT_SIZE;return queue;
}void queue_destroy(Queue* q) {free(q->elements); //释放的是手动malloc的内容free(q);
}//自动扩容
void grow_capacity(Queue* q) {if (q->size >= MAX_SIZE) {printf("Error: push failed, because queue size has reached MAX_SIZE.\n");printf("size = %d, capacity = %d, MAX_SIZE = %d\n", q->size, q->capacity, MAX_SIZE);exit(-1);}int new_capacity = (q->capacity << 1) < MAX_SIZE ? (q->capacity << 1) : MAX_SIZE;E* new_arr = calloc(new_capacity, sizeof(E));if (!new_arr) {printf("calloc failed of new_arr in grow_capacity.\n");exit(-1);}for (int i = 0; i < q->size; i++) {new_arr[i] = q->elements[q->front];q->front = (q->front + 1) % q->capacity;}E* temp = q->elements;free(temp);q->elements = new_arr;q->front = 0;q->rear = q->size;  //下一个要插入元素的位置，目前为空q->capacity = new_capacity;
}void queue_push(Queue* q, E val) {if (q->size == q->capacity) {grow_capacity(q); //自动扩容}q->elements[q->rear] = val;q->rear = (q->rear + 1) % q->capacity;q->size++;
}E queue_pop(Queue* q) {if (queue_empty(q)) {printf("Error: pop failed, because queue is empty.\n");exit(-1);}int ret_val = q->elements[q->front];q->front = (q->front + 1) % q->capacity;q->size--;return ret_val;
}E queue_peek(Queue* q) {if (queue_empty(q)) {printf("Error: peek failed, because queue is empty.\n");exit(-1);}return q->elements[q->front];
}bool queue_empty(Queue* q) {return q->size == 0;
}

//main.c

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include "queue.h"//单元测试
int main(void) {Queue* q = queue_create();queue_push(q, 1);queue_push(q, 2);queue_push(q, 3);queue_push(q, 4);return 0;
}

(4)队列的应用

(1)缓冲：①打印缓冲区 ②秒杀队列(有界队列) ③消息队列 (中间件) (协调分布式)
(2)广度优先搜索 BFS：社交软件三度好友、树的层次遍历

5.哈希表

(1)哈希表的提出原因

(1)用数组表示键值对，限制：
①键的取值范围很小
②键可以很容易地转换成数组的下标
(2)若不满足上述两个限制条件，则引入了哈希表来表示 key-value数据

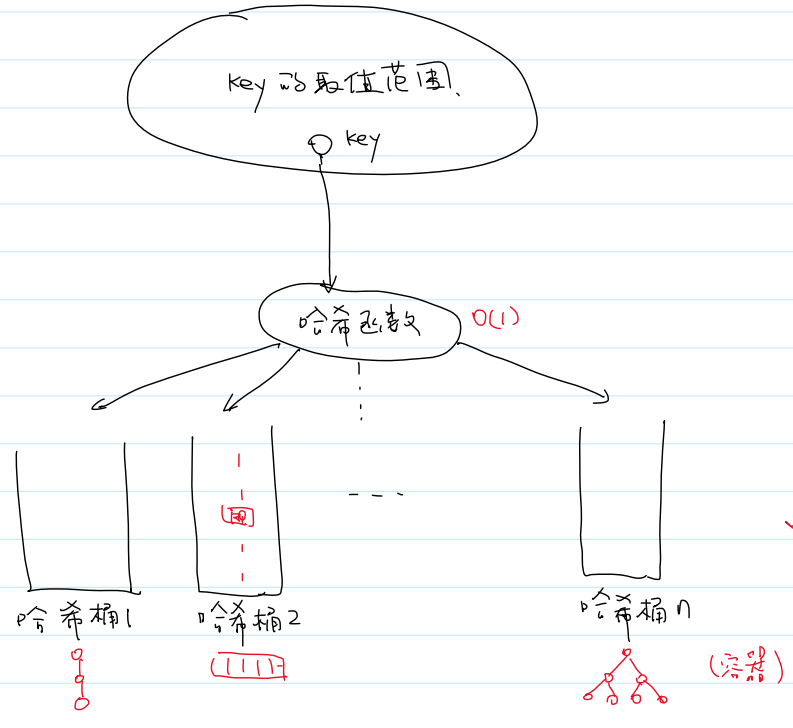
(2)哈希表的模型

①key的取值范围
②哈希函数：时间复杂度O(1)
③哈希桶
(同一个哈希表，可以用不同数据结构的哈希桶：链表、数组、红黑树)

(3)哈希表的基本操作

(1)增加：put(key,val)，给一个key，通过哈希函数，添加到对应的哈希桶中
(2)删除：delete(key)，根据key来删除键值对
(3)查找：val = get(key)
(4)遍历：依次遍历每一个哈希桶

(4)哈希表的理论设计：哈希函数、哈希桶

(1)哈希函数
哈希函数作为数据的指纹

性能非常好的哈希函数的性质：
①速度快 ：O(1)
②哈希值(键值)尽量平均分布
③哈希碰撞的概率非常低 (哈希值→指纹)
④对数据非常敏感
⑤逆向非常困难：不能通过hash值→data，只能data→hash值

哈希函数就是在模仿等概率随机事件

(2)哈希桶：处理哈希冲突，是一种“逻辑结构”
①开放地址法：
i.线性探测法
ii.平方探测法
iii.再散列法 (多个哈希函数，冲突了就用下一个哈希函数)

查找跳转链接：https://blog.csdn.net/Edward1027/article/details/131129113

②拉链法：
拉链法的实现

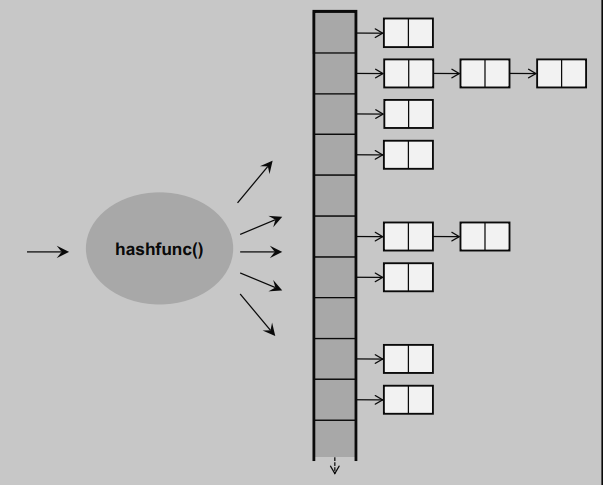
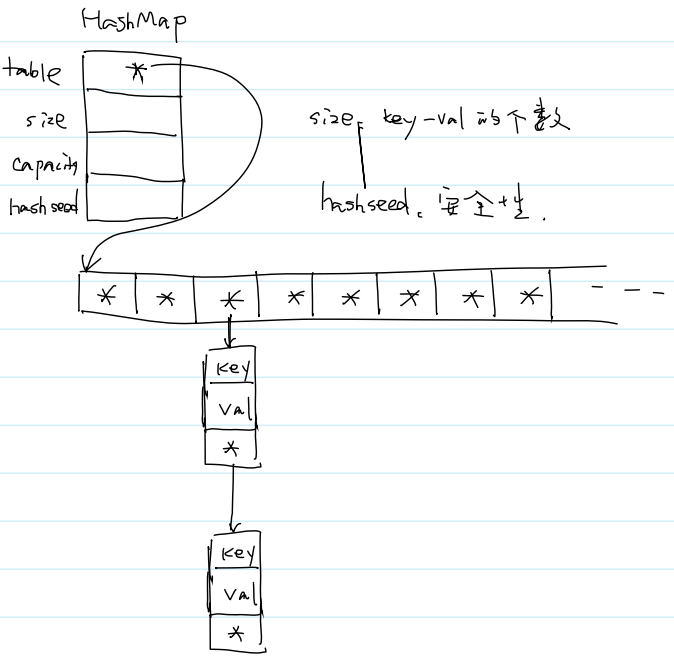
table里存放的是指针。若为NULL则下方无链表，若不为NULL，则为链表的起始地址，即链表头结点的地址。

当结点去掉value，只有key时，哈希表就从存储键值对变成了只存key，即集合

(5)哈希表的具体实现 ：拉链法

(1)构造 create

HashMap* hashmap_create(void) {HashMap* map = malloc(sizeof(HashMap));map->table = calloc(DEFAULT_CAPACITY, sizeof(Node*));map->size = 0;map->capacity = DEFAULT_CAPACITY;map->hashseed = time(NULL);return map;
}

(2)析构 destroy

void hashmap_destroy(HashMap* map) {//1.释放所有的结点(遍历哈希表)for (int i = 0; i < map->capacity; i++) {Node* curr = map->table[i];while (curr) {Node* next = curr->next;free(curr);curr = next;} // curr == NULL}//2.释放动态数组free(map->table);//3.释放HashMap结构体free(map);
}

(3)增加 put

// 如果key不存在：则添加(key, val)。如果key存在，更新key关联的值，并返回原来关联的值。
//put：返回旧值,若是新结点则返回NULL
V hashmap_put(HashMap* map, K key, V val) {//对key进行哈希，判断key在哪个哈希桶中(哪一条链表中)int idx = hash(key, strlen(key), map->hashseed) % map->capacity;//遍历链表Node* curr = map->table[idx];while (curr) {if (strcmp(curr->key, key) == 0) {//b.更新key关联的值，并返回原来的值V oldval = curr->val;curr->val = val;return oldval;}curr = curr->next;}//a.添加一个结点保存键值对 key-val，并返回NULL//判断扩容:如果达到负载因子，则扩容if( ((float)map->size+1)/map->capacity > LOAD_FACTOR){grow_capacity(map);idx = hash(key, strlen(key), map->hashseed) % map->capacity; //重新计算索引}Node* new_node = malloc(sizeof(Node));new_node->key = key;new_node->val = val;//头插法new_node->next = map->table[idx];map->table[idx] = new_node;map->size++;return NULL;
}

(4)查找 get

V hashmap_get(HashMap* map, K key) {//对key进行哈希，判断key在哪个哈希桶中int idx = hash(key, strlen(key), map->hashseed) % map->capacity;//遍历链表Node* curr = map->table[idx];while (curr) {if (strcmp(curr->key, key) == 0) {return curr->val;}curr = curr->next;} //curr == NULLreturn NULL;
}

(5)删除 delete

//删除键值对，如果key不存在，则什么也不做
void hashmap_delete(HashMap* map, K key) {//对key进行哈希，判断key在哪个哈希桶中int idx = hash(key, strlen(key), map->hashseed) % map->capacity;//遍历链表Node* prev = NULL;Node* curr = map->table[idx];while (curr) {if (strcmp(curr->key, key) == 0) {//删除curr结点if (prev == NULL) {map->table[idx] = curr->next;}else{prev->next = curr->next;}free(curr);map->size--;return;}prev = curr;curr = curr->next;} // curr == NULL
}

(6)哈希表的扩容

void grow_capacity(HashMap* map) {int new_capacity = 2 * map->capacity;Node** new_table = calloc(new_capacity, sizeof(Node*));  if (!new_table) {printf("calloc failed of new_arr in grow_capacity\n");exit(1);}//重新映射(rehash)map->hashseed = time(NULL)-10086;for (int i = 0; i < map->capacity; i++) {Node* curr = map->table[i];      while (curr) {Node* next = curr->next;//使用新的容量重新计算哈希值并找到新的索引int new_idx = hash(curr->key, strlen(curr->key), map->hashseed) % new_capacity;//将当前节点插入到新表的相应位置,头插法curr->next = new_table[new_idx];new_table[new_idx] = curr;curr = next;}}//释放旧的表free(map->table);//更新结构体信息map->capacity = new_capacity;map->table = new_table;return;
}

(7)完整代码
//HashMap.h

#include <stdint.h>// HashMap.h
typedef char* K;
typedef char* V;typedef struct node {K key;V val;struct node* next;
} Node;typedef struct {Node** table;int size;     //实际大小int capacity; //最大容量uint32_t hashseed;
} HashMap;HashMap* hashmap_create();
void hashmap_destroy(HashMap* map);
V hashmap_put(HashMap* map, K key, V val);
V hashmap_get(HashMap* map, K key);
void hashmap_delete(HashMap* map, K key);
static uint32_t hash(const void* key, int len, uint32_t seed);

//HashMap.c

#include "HashMap.h"
#include <stdlib.h>
#include <time.h>
#include <stdio.h>#define DEFAULT_CAPACITY 8
#define LOAD_FACTOR 0.75HashMap* hashmap_create(void) {HashMap* map = malloc(sizeof(HashMap));map->table = calloc(DEFAULT_CAPACITY, sizeof(Node*));map->size = 0;map->capacity = DEFAULT_CAPACITY;map->hashseed = time(NULL);return map;
}void hashmap_destroy(HashMap* map) {//1.释放所有的结点(遍历哈希表)for (int i = 0; i < map->capacity; i++) {Node* curr = map->table[i];         while (curr) {Node* next = curr->next;free(curr);curr = next;} // curr == NULL}//2.释放动态数组free(map->table);//3.释放HashMap结构体free(map);
}/* murmurhash2 */
// key: 关键字的地址
// len: 关键字的字节长度
// seed: 哈希种子，避免攻击
static uint32_t hash(const void* key, int len, uint32_t seed) {const uint32_t m = 0x5bd1e995;const int r = 24;uint32_t h = seed ^ len;const unsigned char* data = (const unsigned char*)key;while (len >= 4) {uint32_t k = *(uint32_t*)data;k *= m;k ^= k >> r;k *= m;h *= m;h ^= k;data += 4;len -= 4;}switch (len){case 3: h ^= data[2] << 16;case 2: h ^= data[1] << 8;case 1: h ^= data[0];h *= m;};h ^= h >> 13;h *= m;h ^= h >> 15;return h;
}void grow_capacity(HashMap* map) {int new_capacity = 2 * map->capacity;Node** new_table = calloc(new_capacity, sizeof(Node*));  if (!new_table) {printf("calloc failed of new_arr in grow_capacity\n");exit(1);}//重新映射(rehash)map->hashseed = time(NULL)-10086;for (int i = 0; i < map->capacity; i++) {Node* curr = map->table[i];      while (curr) {Node* next = curr->next;//使用新的容量重新计算哈希值并找到新的索引int new_idx = hash(curr->key, strlen(curr->key), map->hashseed) % new_capacity;//将当前节点插入到新表的相应位置,头插法curr->next = new_table[new_idx];new_table[new_idx] = curr;curr = next;}}//释放旧的表free(map->table);//更新结构体信息map->capacity = new_capacity;map->table = new_table;return;
}// 如果key不存在：则添加(key, val)。如果key存在，更新key关联的值，并返回原来关联的值。
//put：返回旧值,若是新结点则返回NULL
V hashmap_put(HashMap* map, K key, V val) {//对key进行哈希，判断key在哪个哈希桶中(哪一条链表中)int idx = hash(key, strlen(key), map->hashseed) % map->capacity;//遍历链表Node* curr = map->table[idx];while (curr) {if (strcmp(curr->key, key) == 0) {//b.更新key关联的值，并返回原来的值V oldval = curr->val;curr->val = val;return oldval;}curr = curr->next;}//a.添加一个结点保存键值对 key-val，并返回NULL//判断扩容:如果达到负载因子，则扩容if( ((float)map->size+1)/map->capacity > LOAD_FACTOR){grow_capacity(map);idx = hash(key, strlen(key), map->hashseed) % map->capacity; //重新计算索引}Node* new_node = malloc(sizeof(Node));new_node->key = key;new_node->val = val;//头插法new_node->next = map->table[idx];map->table[idx] = new_node;map->size++;return NULL;
}V hashmap_get(HashMap* map, K key) {//对key进行哈希，判断key在哪个哈希桶中int idx = hash(key, strlen(key), map->hashseed) % map->capacity;//遍历链表Node* curr = map->table[idx];while (curr) {if (strcmp(curr->key, key) == 0) {return curr->val;}curr = curr->next;} //curr == NULLreturn NULL;
}//删除键值对，如果key不存在，则什么也不做
void hashmap_delete(HashMap* map, K key) {//对key进行哈希，判断key在哪个哈希桶中int idx = hash(key, strlen(key), map->hashseed) % map->capacity;//遍历链表Node* prev = NULL;Node* curr = map->table[idx];while (curr) {if (strcmp(curr->key, key) == 0) {//删除curr结点if (prev == NULL) {map->table[idx] = curr->next;}else{prev->next = curr->next;}free(curr);map->size--;return;}prev = curr;curr = curr->next;} // curr == NULL
}

//main.c

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include "HashMap.h"int main(void) {//1.创建空的哈希表HashMap* map = hashmap_create();//2.添加键值对hashmap_put(map, "liuqiangdong", "zhangzetian");hashmap_put(map, "wangbaoqiang", "marong");hashmap_put(map, "wenzhang", "mayili");hashmap_put(map, "jianailiang", "lixiaolu");hashmap_delete(map, "liuqiangdong");hashmap_delete(map, "peanut");hashmap_destroy(map);return 0;
}

(6)性能分析

get：O(L)
put：O(L)
delete：O(L)

当加载因子足够小，就认为是O(1)

加载因子/装填因子(Load Factor) 一般为0.75

哈希表是用空间换时间的数据结构

(7)哈希表的应用：存储键值对数据

举例：Redis(C语言实现)，是内存数据库，是键值对数据库，底层大量使用了哈希表。用Redis作缓存。

6.位图

(1)模型

位的数组。位图是内存紧凑的数据结构

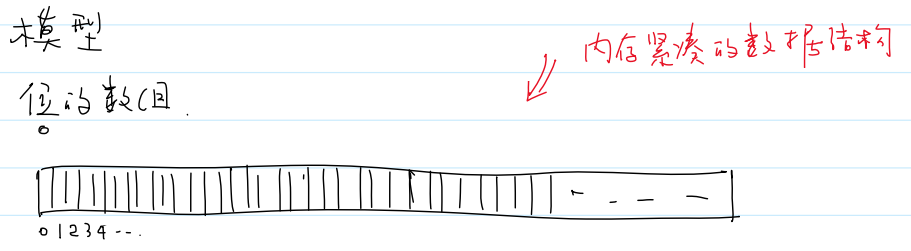
Q：为什么需要构建一个专门的数据结构来表示位的数组？
A：计算机的最小寻址单元是字节，而不是位

(2)基本操作

(1)增加：set，将某一位置为1
(2)删除：①unset，将某一位置为0   ②clear，将所有位置0
(3)查找：isset，检查某一位是否为1
(4)遍历

(3)实现

(1)Word(uint32_t)：①大小是确定的 ②无符号整数
(2)定义宏：
#define BITS_PER_WORD 32   //一个字有多少比特
#define BITMAP_SHIFT 5
#define BITMAP_MASK 0x1F   //取余，对32取余
#define BITMAP_SIZE(bits) (bits+BITS_PER_WORD-1) >> BITMAP_SHIFT   //存这些位需要大？ 向下取整变向上取整

//BitMap.h

// BitMap.h
#include <stdint.h>
#include <stdlib.h>
#include <stdbool.h>typedef struct {//uint32_t：1.大小确定,是32位  2.无符号数  (这里不能用int，因为int类型可能32位可能64位，不同系统大小不同)uint32_t* array;  //array 是动态数组size_t bits;     //number of bits in the array
} BitMap;BitMap* bitmap_create(size_t bits);
void bitmap_destroy(BitMap* bm);
void bitmap_set(BitMap* bm, size_t n); // n is a bit index
void bitmap_unset(BitMap* bm, size_t n);
bool bitmap_isset(BitMap* bm, size_t n);
void bitmap_clear(BitMap* bm);

//BitMap.c

#include "BitMap.h"
#include <stdlib.h>
#include <stdint.h>
#include <stdlib.h>
#include <string.h>
#include <stdio.h>#define BITS_PER_WORD 32
#define BITMAP_SHIFT 5  
#define BITMAP_MASK 0X1F
#define BITMAP_SIZE(bits)  ((bits+BITS_PER_WORD-1) >> BITMAP_SHIFT) //存储bits位, 需要多少个字 wordtypedef uint32_t Word;// bits 是 位图的长度
BitMap* bitmap_create(size_t bits) {BitMap* bm = malloc(sizeof(BitMap));bm->array = (Word*)calloc(BITMAP_SIZE(bits), sizeof(Word));bm->bits = bits;return bm;
}void destroy(BitMap* bm) {free(bm->array);free(bm);
}void grow_capacity(BitMap* bm, size_t bits) {//位图:内存紧凑的数据结构//扩容策略: 需要多大，就申请多大的内存空间uint32_t* new_array = realloc(bm->array, BITMAP_SIZE(bits) * sizeof(Word));if (!new_array) {printf("Error: realloc failed in grow_capacity\n");exit(1);}bm->array = new_array;//将扩容的部分置为0int bytes = (BITMAP_SIZE(bits) - BITMAP_SIZE(bm->bits)) * sizeof(Word);memset(bm->array + BITMAP_SIZE(bm->bits), 0, bytes);
}//设置索引为n的位
//100, 32*4 = 128
void bitmap_set(BitMap* bm, size_t n) {if (n >= bm->bits) {if (BITMAP_SIZE(n + 1) > BITMAP_SIZE(bm->bits)) {//扩容grow_capacity(bm, n + 1);}bm->bits = n + 1;}//设置第n位//如何表示第n位 (word,offset)size_t word = n >> BITMAP_SHIFT;size_t offset = n & BITMAP_MASK;bm->array[word] |= (0x1 << offset);
}void bitmap_unset(BitMap* bm, size_t n) {if (n >= bm->bits) {return;}//找到第n位 (word,offset)size_t word = n >> BITMAP_SHIFT;size_t offset = n & BITMAP_MASK;return bm->array[word] & (0x1 << offset);
}bool bitmap_isset(BitMap* bm, size_t n) {if (n >= bm->bits) {return false;}//找到第n位 (word, offset)size_t word = n >> BITMAP_SHIFT;size_t offset = n & BITMAP_MASK;return bm->array[word] & (0x1 << offset);
}void bitmap_clear(BitMap* bm) {size_t bytes = BITMAP_SIZE(bm->bits) * sizeof(Word);memset(bm->array, 0, bytes);
}

//main.c

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include "BitMap.h"int main(void) {BitMap* bm = bitmap_create(100);bitmap_set(bm, 9);bitmap_set(bm, 5);bitmap_set(bm, 2);bitmap_set(bm, 7);bitmap_set(bm, 120);bitmap_set(bm, 128);//bitmap_unset(bm, 9);//bitmap_unset(bm, 5);//bitmap_unset(bm, 2);//bitmap_unset(bm, 7);//bitmap_unset(bm, 10);// printf("bitmap_isset(bm, 7) = %s\n", bitmap_isset(bm, 7) ? "true" : "false");// printf("bitmap_isset(bm, 10) = %s\n", bitmap_isset(bm, 10) ? "true" : "false");bitmap_clear(bm);return 0;
}

(4)位图的应用

位图的特点：内存紧凑、可以存储两种状态
①存储两种状态 (内存吃紧的情况下，数据量很大)：QQ10亿用户，存储每一位用户的在线状态(是/否)
②排序并去重：直接把对应数字的位置1，相当于去重了，再遍历位图把为1的摘出来

7.二叉树

(1)定义

二叉树的定义：每一个结点的度≤2 (度：结点的孩子的数目)

(2)二叉树的特殊形态

1.完全二叉树：若二叉树的深度为 h，除第 h 层外，其它各层(1～h-1)的结点数目都达
到最大值，第 h 层的结点都连续排列在最左边，这样的二叉树就是完全二叉树。

2.满二叉树：每一层的结点数目都达到最大值(包括最下面一层) [满二叉树真包含于完全二叉树]

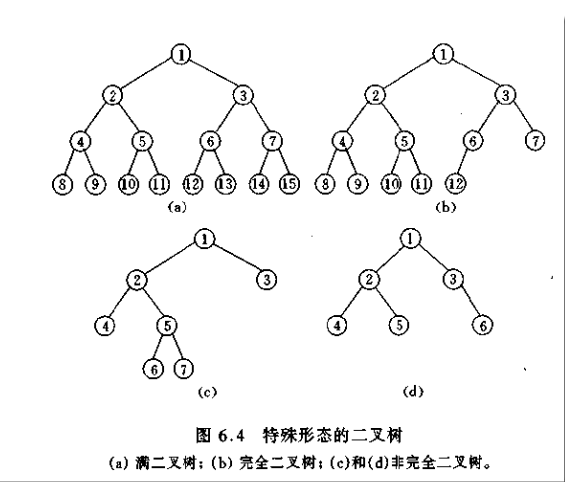
3.二叉搜索树 (BST，Binary Search Tree)
又叫二叉排序树，要求树中的结点可以按照某个规则进行比较，其定义如下：
①左子树中所有结点的 key 值都比根结点的 key 值小，并且左子树也是二叉搜索树。
②右子树中所有结点的 key 值都比根结点的 key 值大，并且右子树也是二叉搜索树。

(3)二叉搜索树BST的实现

查找路径：一条带选择的链表，尾插法

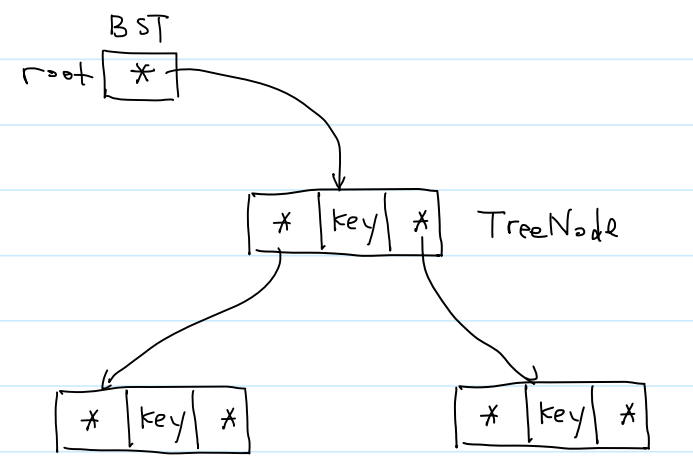
(0)结构体定义

①以前王道书应试的做法，就是直接在第一个结构体最后一行加上 *BST
②之所以把结构体指针 TreeNode* 另起一个结构体，就是为了方便后续扩展。可能BST结构体中还要加入size、height等成员。

typedef int K;typedef struct tree_node {K key;struct tree_node* left;struct tree_node* right;
} TreeNode;typedef struct {TreeNode* root;
} BST;

①创建：create

BST* bst_create(void) {return calloc(1, sizeof(BST));
}

②增加：BST的插入 insert

③查找：BST的查找 search

TreeNode* bst_search(BST* tree, K key) {TreeNode* curr = tree->root; //申请一个树结点指针，指向根结点while (curr) {int cmp = key - curr->key;if (cmp < 0) {			 //目标值 < 当前值curr = curr->left;   //向左走}else if (cmp > 0) {      //目标值 > 当前值curr = curr->right;  //向右走 }else {					 //目标值 = 当前值return curr;	     //找到目标，返回当前树结点指针}} // curr == NULLreturn NULL;				 //未找到目标，返回空指针
}

④删除：BST的删除 delete

⑥遍历

1)深度优先遍历：递归，需要函数调用栈

i.前序遍历

前序遍历 / 先序遍历 / 先根遍历
时间复杂度：O(4n)=O(n)

void preorder(TreeNode* root) {//边界条件if (root == NULL) {return;}//递归公式：根左右printf("%d", root->key);preorder(root->left);preorder(root->right);
}//先根遍历：委托(外包)
void bst_preorder(BST* tree) {preorder(tree->root);printf("\n");
}

ii.中序遍历

二叉搜索树的中序遍历是有序的，因此又称为二叉排序树。

void inorder(TreeNode* root) {// 边界条件if (root == NULL) {return;}// 递归公式: 左根右inorder(root->left);       // 遍历左子树printf("%d ", root->key);  // 遍历根结点inorder(root->right);      // 遍历右子树
}//中序遍历：委托(外包)
void bst_inorder(BST* tree) {inorder(tree->root);printf("\n");
}

iii.后序遍历

void postorder(TreeNode* root) {//边界条件if (root == NULL) {return;}//递归公式：左右根postorder(root->left);postorder(root->right);printf("%d ", root->key);
}//后序遍历：委托(外包)
void bst_postorder(BST* tree) {postorder(tree->root);printf("\n");
}

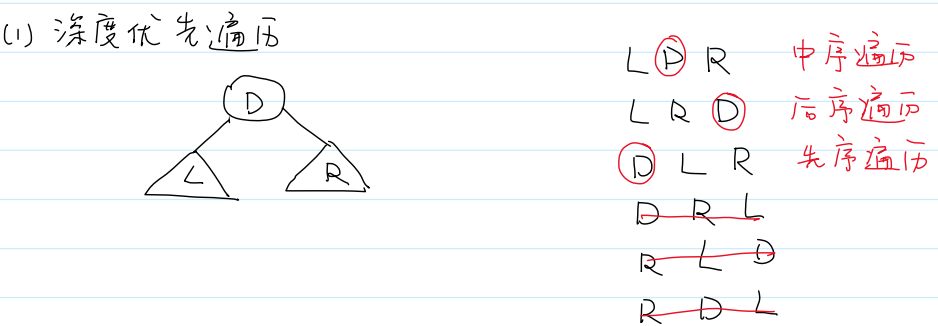
三个结点排列组合有6种遍历，但要求左先于右，故只剩3种

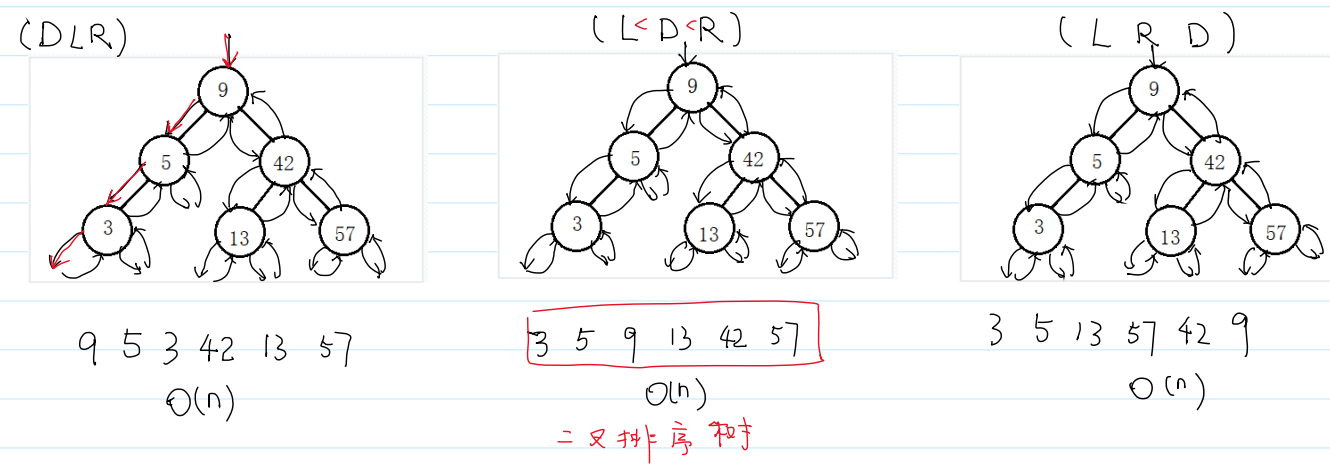
路径完全相同，只是访问顺序不同

2)广度优先遍历：

iv.层序遍历(层次遍历)：需要队列，需要手动创建

1.步骤：
①申请并初始化结点
②根结点入队
③循环判断队列是否非空，若非空，队头结点出队，遍历该结点，若该结点有左孩子，则左孩子入队，若该结点有右孩子，则右孩子入队。

2.具体实现：

// 广度优先遍历:层次遍历
void bst_levelorder(BST* tree) {Queue* q = queue_create();queue_push(q, tree->root);  	    //根结点入队列while (!queue_empty(q)) {		    //判断队列是否为空TreeNode* node = queue_pop(q);  //队头结点出队并遍历printf("%d ", node->key);if (node->left) 	queue_push(q, node->left);if (node->right)	queue_push(q, node->right);} 
}

例题：层序遍历实现分层打印
思路1：记录当前层和下一层的结点数

//分层打印：实现1
void bst_levelorder_fenceng1(BST* tree) {Queue* q = queue_create();queue_push(q, tree->root);int cur_count = 1; //当前层的结点数目int next_count = 0;//下一层的结点数目while (!queue_empty(q)) {TreeNode* node = queue_pop(q);cur_count--;printf("%d ", node->key);if (node->left) {queue_push(q, node->left);next_count++;}if (node->right) {queue_push(q, node->right);next_count++;}//分层打印if (cur_count == 0) {printf("\n");cur_count = next_count;next_count = 0;}}printf("\n");
}

思路2：记录每层的结点数

void bst_levelorder_fenceng2(BST* tree) {Queue* q = queue_create();queue_push(q, tree->root);while (!queue_empty(q)) {int size = q->size;      //记录当前层的结点数for (int i = 0; i < size; i++) {TreeNode* node = queue_pop(q);printf("%d ", node->key);if (node->left) {queue_push(q, node->left);}if (node->right) {queue_push(q, node->right);}}printf("\n");}printf("\n");
}

⑦销毁：destroy

1.后序遍历free

void destroy(TreeNode* root) {  //后序遍历实现释放//边界条件if (root == NULL) {return;}//递归公式：左右根destroy(root->left);destroy(root->right);free(root);            // 释放根节点
}//析构函数1:后序遍历
void bst_destroy(BST* tree) {//0.错误处理if (tree == NULL) {printf("tree == NULL, destroy failed.\n");return;} //1.释放树的结点【委托(外包)】 destroy(tree->root);//2.释放BST结构体free(tree);
}

2.层序遍历free

//析构函数2:层序遍历
void bst_destroy_2(BST* tree) {//容错处理if (!tree || !tree->root)  return;//层序遍历Queue* queue = queue_create();queue_push(queue, tree->root);          // 将根结点入队列while (!queue_empty(queue)) {           // 判断队列是否为空	TreeNode* node = queue_pop(queue);  // 出队列，销毁这个节点if (node->left) {queue_push(queue, node->left);}if (node->right) {queue_push(queue, node->right);}free(node);                         // 释放节点}free(tree);							    // 节点销毁
}

(4)BST性能分析

1.n个结点的BST树的高度为h，h的范围是[log₂n,n]

2.BST的效率：
①插入 insert：O(h)
②删除 delete：O(h)
③查找 search：O(h)

3.BST的优点/使用场景：①保证有序性 ②需要动态添加和删除元素

4.缺陷：不能保证O(logn)的时间复杂度的插入、删除、查找，最坏情况是单支树。因为总朝着一个方向进行操作(删右添左)，性能会退化，缺少调平衡。因此引入了平衡二叉搜索树

5.对比有序数组的效率：
①增：O(n)
②删：O(n)
③查：O(logn)
④遍历：O(n)
有序数组的使用场景：①保证有序性 ②存储静态数据

(5)平衡二叉搜索树

①AVL树

AVL树平衡的定义：对任意一个结点，左子树和右子树的高度之差不超过1
定义严格，导致：①高度比较小 ②每次添加和删除时需要进行的调整较多

故 AVL树，查找效率高，添加和删除效率低于RBT

②红黑树 RBT

1.红黑树平衡的定义：整棵树的高度为O(logn)
定义比较宽松，导致：①高度比较高 ②每次添加和删除时需要进行的调整操作少

故 红黑树，添加和删除效率高，查找的效率低于AVL树。

在不断的实验中发现，红黑树的效率总体来说高于AVL树。故日常生产更多使用红黑树。

2.模型
提升，同一层的，类似原子间作用力
①3-结点有两种表示方式：提升最左边或者提升最右边
②4-结点只有一种表示方式，就是高度最低的这种，高度为2。其余高度为3的表示方式都是错的。即不能有两条连续的红色边

但边是逻辑结构，实际不存在，那么如何表示边的颜色呢？
可以考虑用结点来表示边的颜色。
那么用父结点还是孩子结点来表示边的颜色呢？
答案是用孩子结点来表示边的颜色。因为父结点对应两条边，孩子结点向上只有一条边。

黑高就是2-3-4树的高度

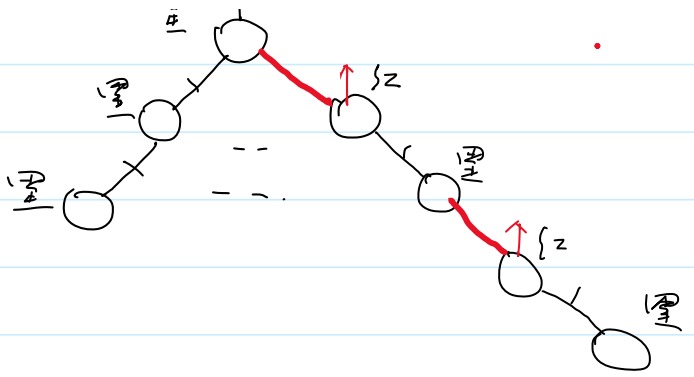
红黑树的高度最多是黑高的2倍。也是logn级别

3.基本操作 (和BST一样)

(5)B树

①2-3-4树 (四阶B树)

1.模型

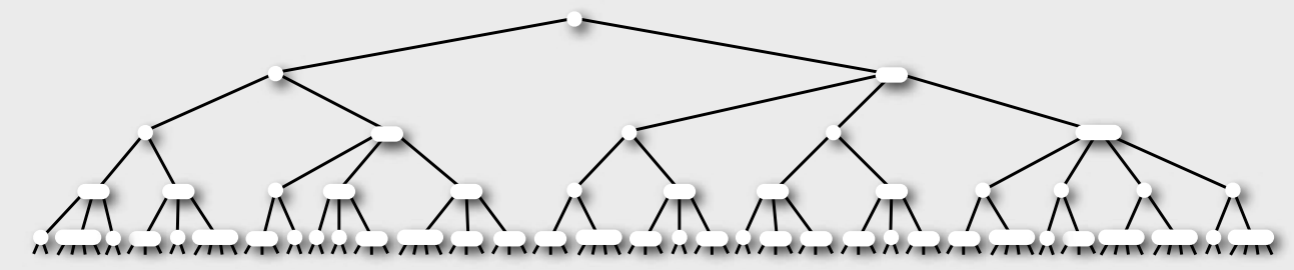
2.性质
①根节点分裂，树高才+1
②动态保持完美平衡

3.4-结点分裂
①自底向上(Bayer, 1972)
② 自顶向下(Guibas-Sedgewick, 1978)：遇到4-结点就分裂，当前结点不是4-结点。

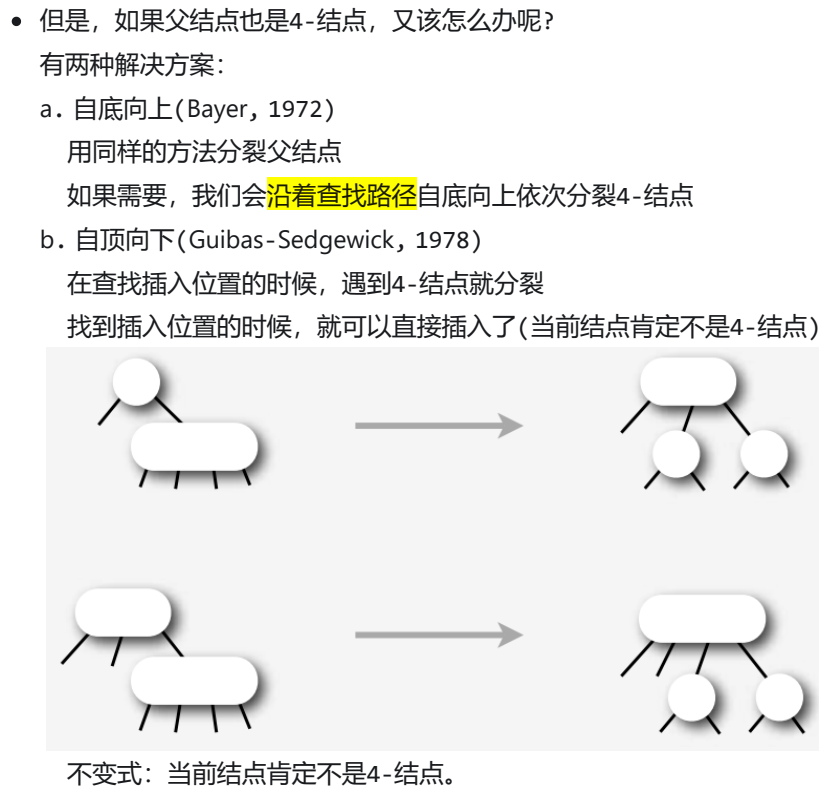
4.实现
红黑树是2-3-4树的具体实现，2-3-4树是一种模型

(6)二叉搜索树的应用

(7)代码缩进的层次越高，代码的复杂度就越高，可读性越差

循环的两个点：循环退出点、循环不变式
递归的两个核心点：边界条件、递归公式

(十二) 排序和二分查找

1.二分查找

1.前提：
①有序 ：具有某种顺序，不一定非得是 从小到大或者从大到小，比如循环有序
②数组：随机查找。通过每次比较，可以丢掉几乎一半的区间。

2.性能：O(logn)

3.作用：
比起顺序查找，二分查找大量减少了比较操作 。
即使是比较小的数组，也可能因为存储的元素较大(长的字符串、大的集合)，导致比较很慢。也可以用二分查找减少比较次数。

4.实现：2种实现 + 4种变式

(1)递归实现

//递归实现的子函数
int binarysearch_1(int arr[], int left, int right, int key) {//边界条件if (left > right)   return -1;//递归公式//int mid = (left + right) / 2;int mid = left + (right-left)/2;  //避免整数溢出    if (key < arr[mid]) {                                 //目标值 < 中值  return binarysearch_1(arr, left, mid - 1, key);	  //往左走 } else if (key > arr[mid]) {                          //目标值 > 中值return binarysearch_1(arr, mid + 1, right, key);  //往右走} else {					                          //目标值 = 中值	return mid;										  //直接返回下标(索引)}
}//1.二分查找的递归实现：返回的是key的索引
int BinarySearch_1(int arr[], int n, int key) {//(1)数组不好递归，区间好递归 (2)封装，避免用户手动输入区间，丑陋的接口return binarysearch_1(arr, 0, n - 1, key);     //闭区间: [0 , n-1]
}

(2)循环实现

//2.二分查找的循环实现
int BinarySearch_2(int arr[], int n, int key) {int left = 0, right = n - 1;while (left <= right) {//int mid = (left + right) / 2;int mid = left + (right-left >> 1);  //避免整数溢出  if (key < arr[mid]) {        //目标值 < 中间值right = mid - 1;         //向左走} else if (key > arr[mid]) { //目标值 > 中间值left = mid + 1;          //向右走} else {					 //目标值 = 中间值return mid;			     //返回中间值的索引}}return -1;         //没找到，返回-1，表示 key 不存在
}

5.二分查找的4种变种
(1)查找第一个与key值相等的元素

//查找第一个和key值相等的元素
int BinarySearch_3(int arr[], int n, int key) {int left = 0, right = n - 1;while (left <= right) {//int mid = (left + right) / 2;int mid = left + (right-left >> 1);  //避免整数溢出  if (key < arr[mid]) {right = mid - 1;} else if (key > arr[mid]) {left = mid + 1;} else {  //相等,但是要找从左数第一个与key值相等的if(mid == left || arr[mid-1] < key) right = mid - 1;   //区间向左缩小1}}return -1;
}

(2)查找最后一个与key值相等的元素

//4.查找最后一个和key值相等的元素
int BinarySearch_4(int arr[], int n, int key) {int left = 0, right = n - 1;while (left <= right) {int mid = left + (right-left >> 1);  //避免整数溢出  if (key < arr[mid]) {right = mid - 1;}else if (key > arr[mid]) {left = mid + 1;}else {  // key == arr[mid],但是要找从左数最后一个与key值相等的if (mid == right || key < arr[mid + 1] ) {return mid;}left = mid + 1;   //区间向右缩小1}}return -1;
}

(3)查找第一个大于等于key值的元素

//5.查找第一个大于等于key值的元素:先向右找到比key大的，再逐步向左走找到第一个
int BinarySearch_5(int arr[], int n, int key) {int left = 0, right = n - 1;while (left <= right) {int mid = left + (right-left >> 1);  //避免整数溢出  if (arr[mid] < key) {left = mid + 1;} else {  // arr[mid] >= keyif (mid == left || arr[mid - 1] < key) {return mid;}right = mid - 1;}}return -1;
}

(4)查找最后一个小于等于key值的元素

//6.查找最后一个小于等于key值的元素：先向左找到比key小的，再逐步向右找到最后一个
int BinarySearch_6(int arr[], int n, int key) {int left = 0, right = n - 1;while (left <= right) {int mid = left + (right-left >> 1);  //避免整数溢出  if (arr[mid] > key) {right = mid - 1;  //向左} else {  //arr[mid] <= keyif (mid == right || arr[mid+1] > key) {return mid;}left = mid + 1; //逐步向右}}return -1;
}

6.具体应用：IP地址归属地查询

2.排序算法分析

0.排序的目的，是方便查找

1.分析/评估算法的能力，比算法的实现更重要

2.如何分析一个排序算法：时间复杂度、空间复杂度、稳定性
(1)时间复杂度：
①最好情况：对应它的应用场景
②最坏情况：算法的下限
③平均情况：
④常数项和低阶项：

(2)空间复杂度：
我们需要重点关注原地排序(store in place)，也就是空间复杂度为 O(1) 的排序。

(3)稳定性：
数据集中"相等"的元素，如果排序前和排序后的相对次序不变，那么这个排序算法
就是稳定的。稳定性是排序算法一个很重要的指标。

3.不同场景选择不同的排序算法 (没有最好的排序算法，只有最合适的排序算法)

3.选择排序

1.思路：
遍历从未排序的元素中，找到最小元素的下标，一趟结束找出最小，进行交换
共n-1趟。每趟重置 j = i+1

2.代码

void SelectionSort(int arr[], int n) {for (int i = 0; i < n-1; i++) {int min_index = i;for (int j = i+1; j < n ; j++) {if (arr[j] < arr[min_index]) {min_index = j;}}swap(&arr[min_index], &arr[i]);}print_array(arr, 10);
}

3.性能分析
(1)时间复杂度：O(n²)
比较次数：n-1 + n-2 + … = $\frac{n(n-1)}{2}$ 。无论初始序列如何，一定会进行n-1趟简单选择排序。一定会比较 $\frac{n(n-1)}{2}$ 次，但是交换次数很少

(2)空间复杂度：O(1)
(3)稳定性：选择排序是不稳定的，因为会发生长距离的交换。例如：

[2, 2', 1]

经过简单选择排序第一轮就变成了

[1, 2', 2]   //2与2'的相对位置发生改变

4.冒泡排序

1.思路：
确定未排序区域。

2.优化：冒泡排序可以提前结束。如果本趟冒泡没有发现逆序对(未发生交换)，则认为整个数组已经有序，可以直接结束。

3.实现

void BubbleSort(int arr[], int n) {for (int i = 0; i < n-1; i++) {for (int j = 0; j < n-1-i; j++) {  //大值从前往后冒泡if (arr[j] > arr[j+1]) {swap(&arr[j], &arr[j+1]);}}//for (int j = n - 1; j > i; j--){     //小值从后往前冒泡//	if (arr[j-1] > arr[j]) {//		swap(&arr[j-1], &arr[j]);//	}//}}print_array(arr, 10);
}

优化：冒泡排序可以提前结束：本趟冒泡没有发现逆序对

void swap(int* a,int* b){int temp = *a;*a = *b;*b = temp;
}void BubbleSort(int arr[],int n){for(int i = 0; i < n-1; i++){ 		//n-1趟bool isSwap = false;   for(int j = n-1; j > i; j--){   //从后向前冒if(arr[j-1] > arr[j]){  	//稳定的，仅交换逆序对swap(&arr[j-1], &arr[j]);isSwap = true;}}if(isSwap == false) return; //优化:某一趟排序未发生交换，冒泡排序可以提前结束}
}

4.性能分析
(1)时间复杂度：O(n²)
①最好情况：原数组有序, O(n)
比较次数：n-1
交换次数：0
②最坏情况：原数组逆序, O(n²)
比较次数：(n-1) + (n-2) + … + 1 = $\frac{n(n-1)}{2}$
交换次数：(n-1) + (n-2) + … + 1 = $\frac{n(n-1)}{2}$
③平均情况：O(n²)
比较次数：大于等于交换的次数，小于等于 $\frac{n(n-1)}{2}$
交换次数：n(n-1)/4 (等于逆序对的个数)

冒泡和插入排序的分析方法一致，性质一模一样。三种情况的时间复杂度相同。
但常数项不同，插入排序的交换仅1次赋值(没有用到swap函数)，而冒泡排序的交换要4次赋值，故同一个O复杂度下，插入排序效率更高。

(2)空间复杂度：O(1)
(3)稳定性：冒泡排序是稳定的，因为只有相邻的逆序对才进行交换，遍历整个未排序区域，将逆序对降低为0

5.插入排序

插入排序(Insertion sort)

1.思路：前半部分是手牌，后半部分是无序的牌堆。从牌堆拿起一张，从手牌最大开始比较，找到第一个小于等于value的元素，插入到它的后面。
插入排序，是从后往前遍历已有序的区域，从有序区域的最后一个开始往前遍历

2.实现

void InsertionSort(int arr[], int n) {for (int i = 1; i < n; i++) {int insertval = arr[i];int j = i - 1;  //从后往前遍历有序区域，从有序区域的最后一个开始while (j >= 0 && arr[j] > insertval) {arr[j + 1] = arr[j]; //元素右移j--;}arr[j + 1] = insertval;}print_array(arr, 10);
}

3.性能分析
(1)时间复杂度：
①最好情况：原数组有序
比较n-1次，交换0次
时间复杂度为O(n)

插入排序，基本有序的数组时间复杂度最低，为O(n)。甚至快过快速排序等。排序 至少需要遍历一遍数组，O(n)的时间复杂度就是最低的了。

②最坏情况：原数组逆序
比较 1+2+3+…+n-1 = $\frac{n(n-1)}{2}$ 次，交换 1+2+3+…+n-1 = $\frac{n(n-1)}{2}$ 次
时间复杂度为O(n²)

③平均情况：O(n²)

(2)空间复杂度：O(1)，原地排序

(3)稳定性：
插入排序是稳定的，因为只交换相邻的逆序对，能保证原来的顺序。

4.使用场景
当数组满足：
①数组长度较小
②原数组基本有序（元素离最终位置相差不远）
插入排序可以达到O(n)的时间复杂度。

插入排序在对几乎已经排好序的数据排序时，效率很高，可以达到线性排序的效率。

6.希尔排序

1.历史地位：希尔排序是第一个时间复杂度低于O(n²)的排序算法

2.思想：
希尔排序，又叫缩小增量排序。

①多人抓牌，每个人手牌有序。人数由多到少
②倒数第二次时，gap = 2，任意元素离最终位置的距离都<2，此时数组已经基本有序。
③最后一次希尔排序gap为1，退化为插入排序。
④减到0结束排序。

减少了长距离一步步交换，减少了移动的次数。长距离交换使得小数可以快速达到最终位置。

希尔排序的效率与 gap 序列相关，希尔本人推荐的 gap 序列为：n/2, n/4, …, 1。
但这个序列并不是最佳的( ╯□╰ )…

3.实现
gap个人轮流抓牌。
加个while循环，所有的1改成gap。

void ShellSort(int arr[], int n) {int gap = n / 2;while (gap != 0) {//组间插入排序for (int i = gap; i < n; i++) {int insertval = arr[i];int j = i - gap;   //遍历有序区域while (j >= 0 && arr[j] > insertval) {arr[j + gap] = arr[j];j -= gap;}arr[j + gap] = insertval;}gap /= 2;}print_array(arr, 10);
}

4.设计的思考：
利用了插入排序的优点( 基本有序时为O(n) )，避免了插入排序的缺点 (元素较小的元素需要长途跋涉的比较才能到达前面。希尔排序设计了长距离交换，使得移动减少。)

5.效率分析：
(1)时间复杂度：和gap序列有关，整体＜O(n²)

(2)空间复杂度：O(1)

(3)稳定性：不稳定
长距离交换可能导致同值的相对位置发生改变

6.比较
希尔排序，相比插入排序：牺牲了稳定性，换取了时间

7.归并排序

(1)分治思想

1.分治思想：

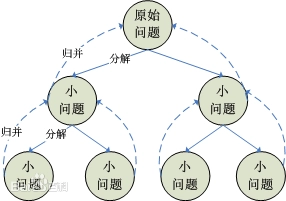
2.分治与递归的关系
①分治思想：算法设计思想
②递归：一种代码实现方式
关系：不同维度的东西，分治的思想一般用递归来实现

3.分治思想的应用：
二分查找、归并、快速排序、矩阵相乘

(2)合并操作：Merge()

1.过程
递归图：

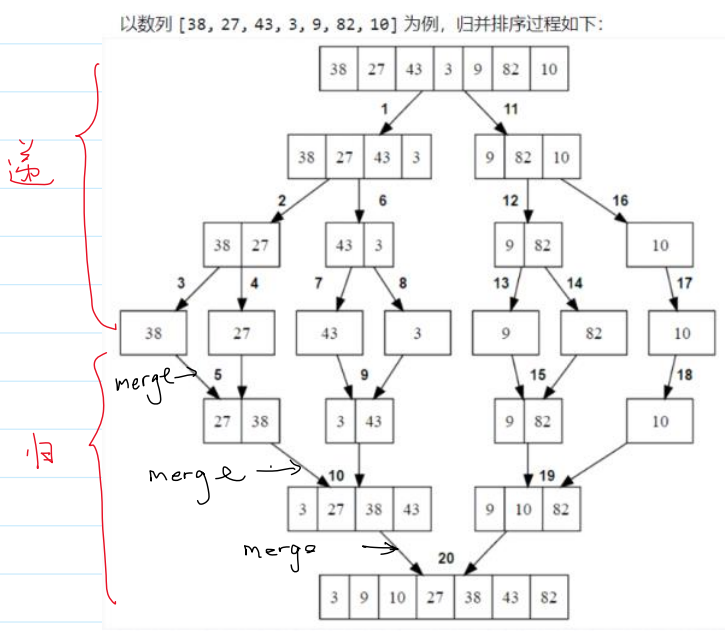
2.实现

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#define N 10void print_array(int arr[], int n) {for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");
}int temp[N];void Merge(int arr[], int left, int mid, int right) {int i = left, j = mid + 1, k = left;//复制for (i = left; i <= right; i++)		temp[i] = arr[i];while (i <= mid && j <= right) {if (temp[i] <= temp[j]) {arr[k++] = temp[i++];}else {arr[k++] = temp[j++];}}while (i <= mid)	arr[k++] = temp[i++];while (j <= right)	arr[k++] = temp[j++];
}void MergeSort(int arr[], int left, int right) {//边界条件if (left >= right)	return;//递归公式int mid = left + (right - left >> 1);MergeSort(arr, left, mid);MergeSort(arr, mid + 1, right);Merge(arr, left, mid, right);
}void merge_sort(int arr[], int n) {MergeSort(arr, 0, n - 1);
}int main(void) {int arr[] = { 10,9,8,7,6,5,4,3,2,1 };merge_sort(arr, N);print_array(arr, N);return 0;
}

3.性能分析
(1)时间复杂度：
归并排序对排序不敏感，任何情况下时间复杂度都是O(nlogn)

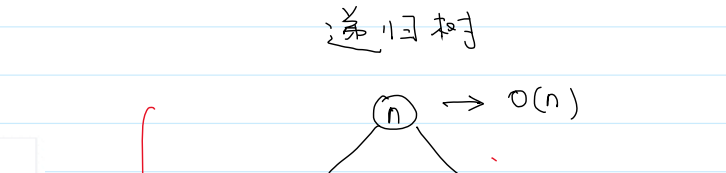
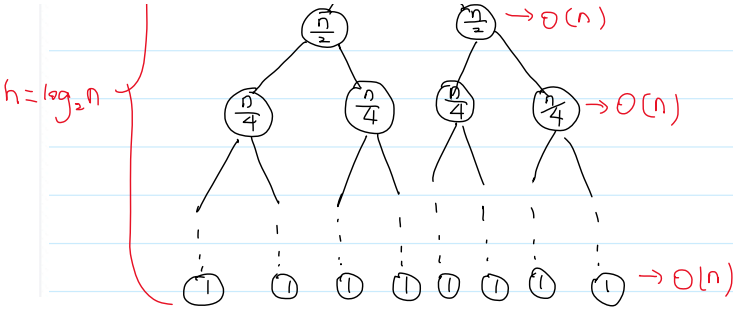
分析：使用递归树，来分析递归程序的时间复杂度

数组长度为n，Merge()是O(n)
递归树深度是log₂n

T(n) = log₂n·O(n) = log₂n·cn = O(nlog₂n) = O(nlogn)

大O表示法不关心底是多少，因为有换底公式

(2)空间复杂度：
递归调用栈O(logn) + 辅助数组O(n) = O(n)
归并排序的空间复杂度太高了，内存消耗很大，不能用于大数组的排序
空间复杂度高是归并排序比较显著的缺陷。

(3)稳定性：
稳定的。arr[i] <= arr[j]

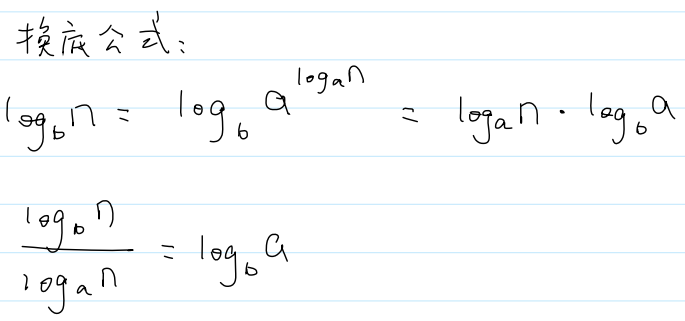
8.快速排序

1.快速排序(Quick sort)是建立在分区操作上的一种高效的排序算法。快速排序也是分治思想的一种典型应用。

2.算法步骤
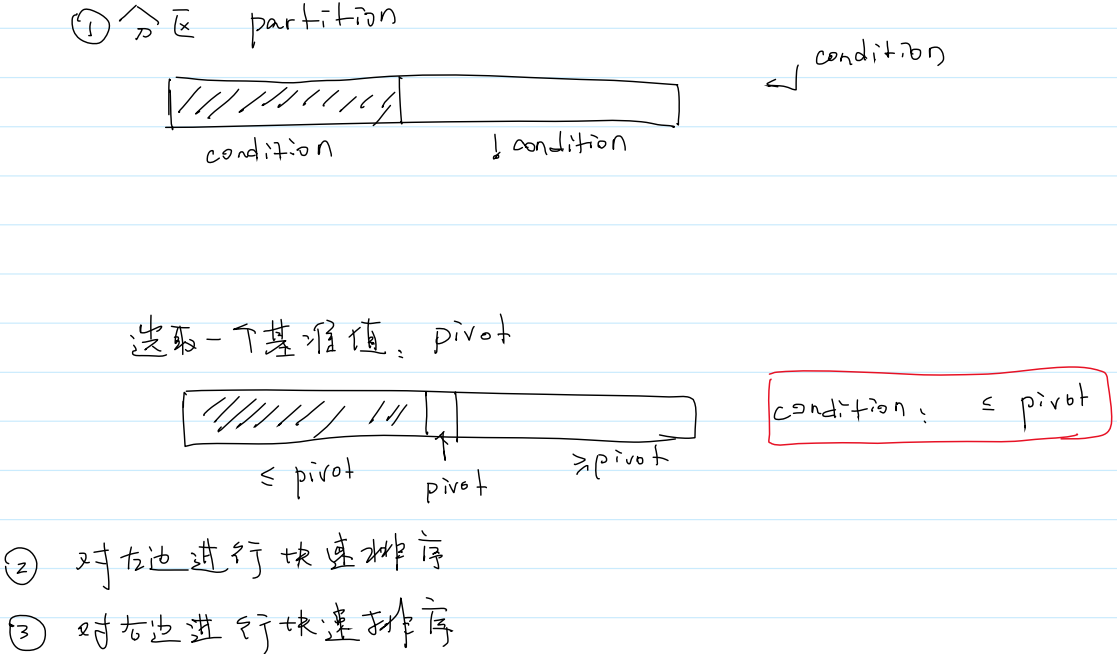
分区操作 Partition

3.实现
(1)如何分区
①单向分区

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <time.h>#define SIZE(a) (sizeof(a)/sizeof(a[0]))
#define SWAP(arr, i, j){    \int t = arr[i];			\arr[i] = arr[j];		\arr[j] = t;				\
}void print_array(int arr[], int n) {for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");
}//花生讲义的单向分区(单向扫描算法)
int partition(int arr[], int left, int right) {// 选取基准值，并将基准值放到最右边int idx = rand() % (right - left + 1) + left;int pivot = arr[idx];SWAP(arr, idx, right);// 分区操作int storeIdx = left;for (int i = left; i < right; i++) {if (arr[i] < pivot) {SWAP(arr, storeIdx, i);storeIdx++;}}SWAP(arr, storeIdx, right);// 返回基准值最终所在的索引return storeIdx;
}void quick_sort_helper(int arr[], int left, int right) {// 边界条件if (left >= right) return;// 递归公式int idx = partition(arr, left, right);quick_sort_helper(arr, left, idx - 1);quick_sort_helper(arr, idx + 1, right);
}void quick_sort(int arr[], int n) {srand(time(NULL));quick_sort_helper(arr, 0, n - 1);
}int main(void) {int arr[] = { 5,4,3,2,1 };quick_sort(arr, 5);print_array(arr, 5);return 0;
}

②双向分区：
考研，划分左右区间。性能最好。
左右两根指针，向中间移动，相遇点即为pivot的位置

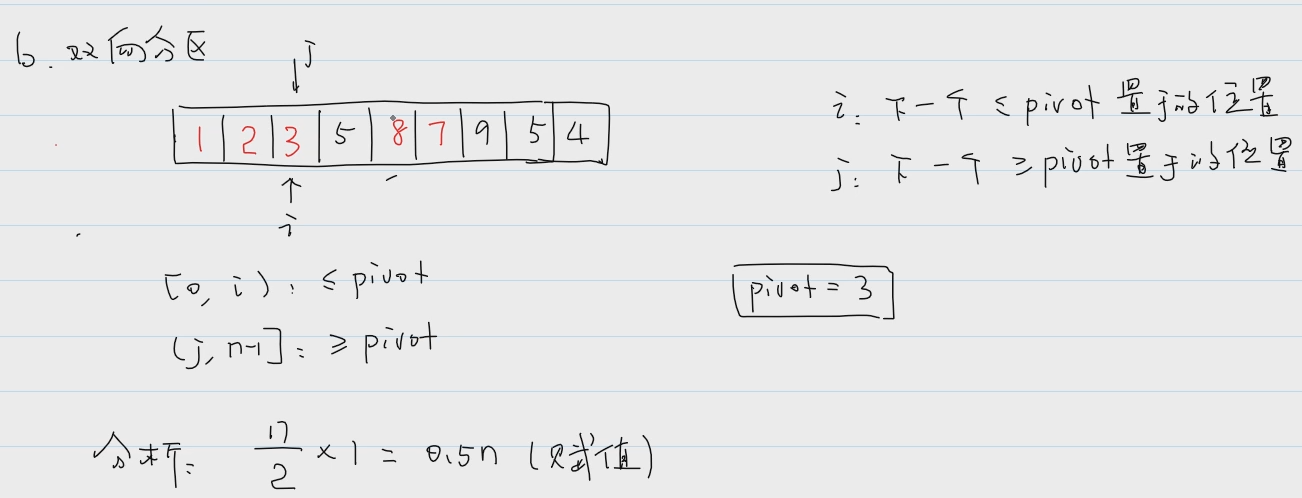
//双向分区(双向扫描)
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#define SIZE(a) (sizeof(a)/sizeof(a[0]))void print_array(int arr[], int n) {for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");
}int Partition(int arr[], int left, int right) {//选取基准值int pivot = arr[left];//双向分区int i = left, j = right;while (i < j) {//先移动j，找＜pivot的元素while (i < j && arr[j] >= pivot) {j--;}  // i == j || arr[j] < pivotarr[i] = arr[j];//再移动i，找>pivot的元素while (i < j && arr[i] <= pivot) {i++;} // i == j || arr[i] > pivotarr[j] = arr[i];} // i == jarr[i] = pivot;return i;
}void QuickSort(int arr[], int left, int right) {//边界条件if (left >= right)	 return;//递归公式int idx = Partition(arr, left, right);print_array(arr, 5);QuickSort(arr, left, idx-1);QuickSort(arr, idx+1, right);
}void quick_sort(int arr[], int n) {//委托的原因：(1)数组不好递归，区间好递归//(2)丑陋的内部设计要封装起来，只暴露一个简单易用的接口给用户QuickSort(arr, 0, n - 1);
}int main(void) {int arr[] = { 5,4,3,2,1 };quick_sort(arr, SIZE(arr));return 0;
}

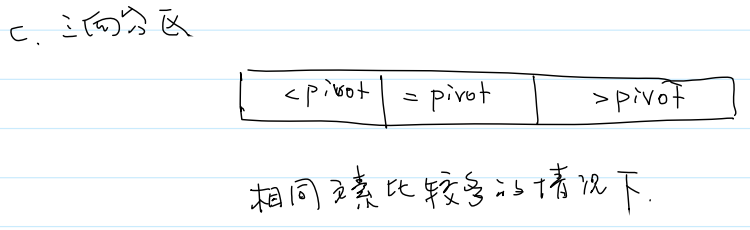
③三向分区：
应用场景：相同元素比较多的情况下
一般情况下三向分区性能弱于单向分区和双向分区，但在相同元素较多时三向分区算法性能较高。
极端情况，当数组元素全部相同时，三向分区算法一次就能结束。

4.性能分析
(1)时间复杂度：
①最好情况：
每次分区，基准值恰好位于中间，每次分区都可以分为大小相等的两份
T(n) = O(n) + T($\frac{n}{2}$) + T($\frac{n}{2}$) = 2T($\frac{n}{2}$)+O(n) = O(nlogn)

②最坏情况：
每次分区，基准值都位于两端
T(n) = O(n) + T(n-1) = cn + T(n-1) = cn + c(n-1) + T(n-2) = c[n+ n-1 + n-2 + … + 1] = $c\frac{n\cdot (n-1)}{2}$= O(n²)

③平均情况：
假设每次分区，都划分成9:1的区间

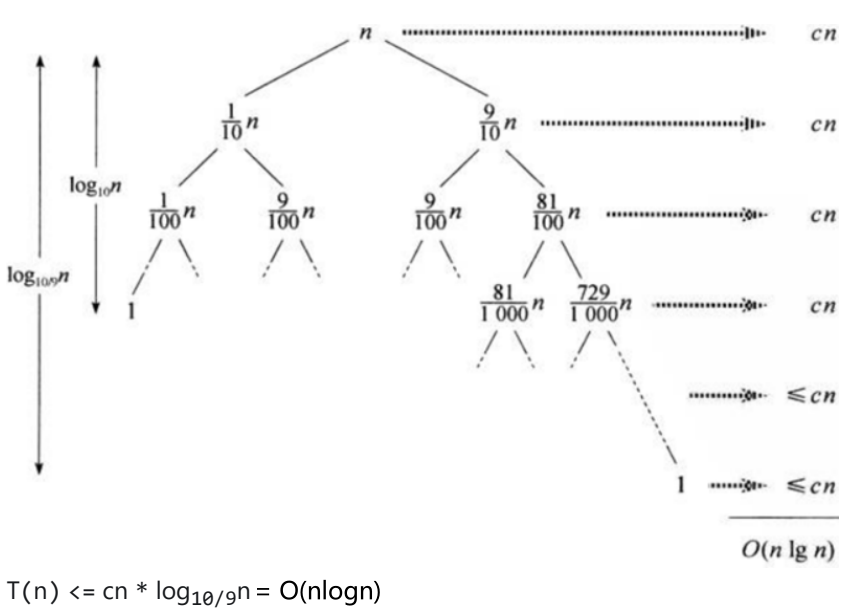
(2)空间复杂度：O(logn)
平均情况下，栈的深度为 O(logn)。

大O表示法，是表示增长趋势，并不是实际大小。O(logn)的实际内存大小，并不一定会大于O(1)，因为常数项可能很大。

(3)稳定性：不稳定
在分区操作中，选取基准值后，我们会将其和最右边的元素进行交换。这可能是一
次长距离的交换，因此快速排序是不稳定的。

5.快排的优化 (改进策略)：
(1)选取合适的基准值：
①随机选取
②选取3到5个元素，选取其中位数

(2)当子区间长度小于等于某个值(≤32，≤64)时，改用插入排序

(3)分区算法：
当区间中相同元素较多时，改用三向分区

9.堆排序

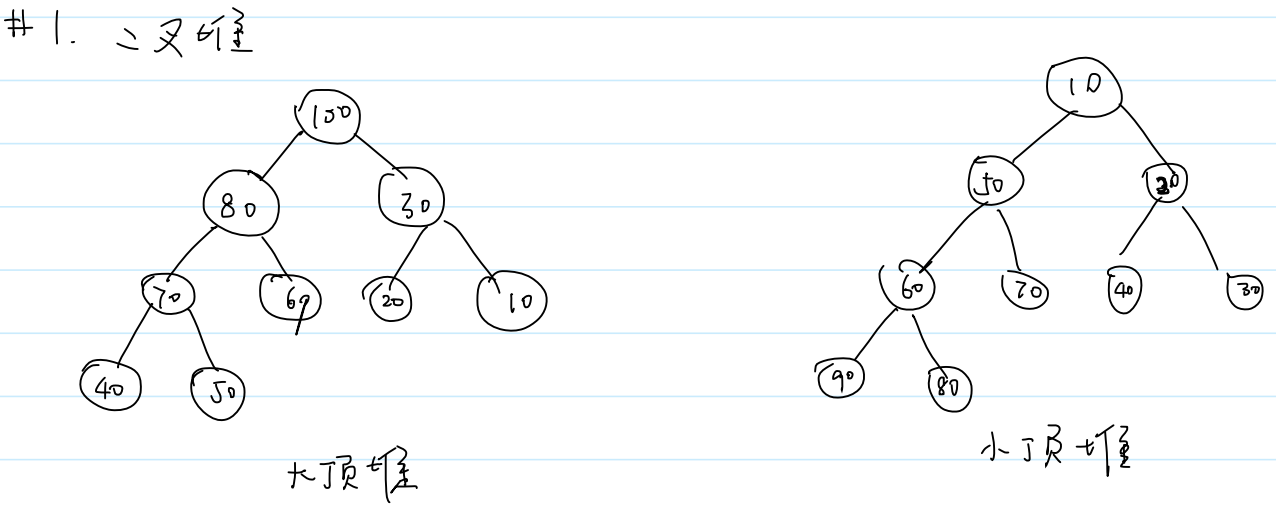
1.二叉堆
(1)大顶堆 (大根堆)
根结点是最大值，左右子树也是大顶堆

(2)小顶堆 (小根堆)
根结点是最小值，左右子树也是小顶堆

2.算法步骤
(1)构建大顶堆

(2)初始化无序区长度 len = n

(3)交换堆顶元素和无序区的最后一个元素，无序区的长度len–。

(4)重新调整成大顶堆，即根结点下坠。重复，直至len == 1。

3.实现：大顶堆

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>#define SWAP(arr, i ,j){	\int temp = arr[i];		\arr[i] = arr[j];		\arr[j] = temp;			\
}void print_array(int arr[], int n) {for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");
}//i：需要调整的结点索引
//n：索引的最大范围
void heapify(int arr[], int i, int n) {while (i < n) {//求三个元素的最大值int lchild = 2 * i + 1;int rchild = 2 * i + 2;int maxIdx = i;if (lchild < n && arr[lchild] > arr[maxIdx]) {maxIdx = lchild;}if (rchild < n && arr[rchild] > arr[maxIdx]) {maxIdx = rchild;}if (maxIdx == i)	break;  //如果最大值是根结点，调整提前结束  SWAP(arr, i, maxIdx);		//如果不是，交换根结点和最大值结点i = maxIdx;					//继续下坠} //i >= n || maxIdx == i
}void build_heap(int arr[], int n) {//找到第一个非叶子结点i: lchild(i) = 2i+1 < n，2i+1 <= n-1, 2i <= n-2， i <= n/2 - 1//从后往前依次构建大顶堆for (int i = n / 2 - 1; i >= 0; i--) {heapify(arr, i, n);}
}void heap_sort(int arr[], int n) {//1.构建大顶堆build_heap(arr, n);//2.初始化无序区的长度int len = n;//3.交换堆顶元素和无序区最后一个元素，直到 len == 1while (len > 1) {SWAP(arr, 0, len-1);len--;heapify(arr, 0, len);} //len == 1
}int main(void) {int arr[] = { 9, 8, 7, 6, 5, 4, 3, 2, 1, 0};heap_sort(arr, 10);print_array(arr, 10);return 0;
}

4.性能分析
(1)时间复杂度：堆排序对数据不敏感，任意情况下均为O(nlogn)

①构建大顶堆 build_heap()：O(n)
②调整堆：(n-1) * logn = O(nlogn)

(2)空间复杂度：O(1)
【没有递归，也没有额外使用数组】

(3)稳定性：
不稳定。父结点与子结点交换，在数组里是远距离交换

归并排序 vs 堆排序：
共同点：都对数据不敏感，时间复杂度都是O(nlogn)
不同点：归并排序空间复杂度O(n)，但稳定；堆排序空间复杂度O(1)，但不稳定。

10.如何设计一个通用的排序算法

出租车很快，但有时候可能堵车
地铁比较稳定，就像堆排序对数据不敏感

洗牌算法：随机打乱数组

完整代码：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <time.h>#define SIZE(a) (sizeof(a)/sizeof(a[0]))
#define SWAP(arr, i ,j){ \int temp = arr[i];   \arr[i] = arr[j];     \arr[j] = temp;		 \
}void print_array(int arr[], int n) {for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");
}//洗牌，随机打乱 【Fisher-Yates洗牌算法】
void shuffle(int arr[], int n) {srand(time(NULL));		// 初始化随机数生成器for (int i = 0; i < n - 1; i++) {// [i, n-1]int j = rand() % (n - i) + i;SWAP(arr, i, j);}
}int main(void) {int arr[] = { 0,1,2,3,4,5,6,7,8,9 };shuffle(arr, SIZE(arr));print_array(arr, SIZE(arr));return 0;
}