1.二叉树的遍历

1.1前序、中序以及后序遍历

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

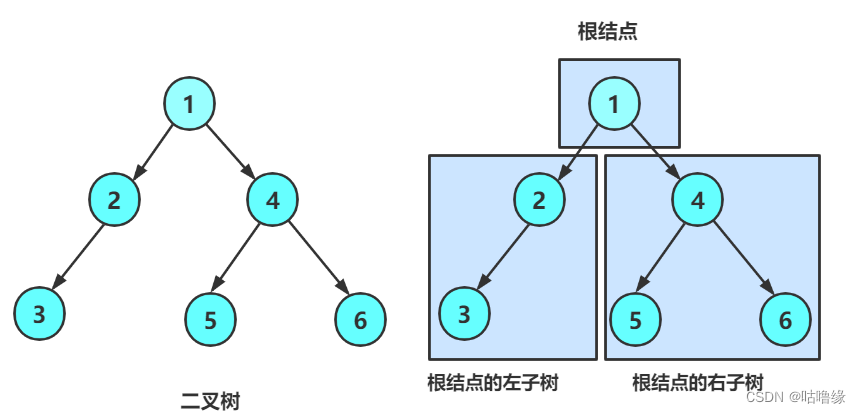
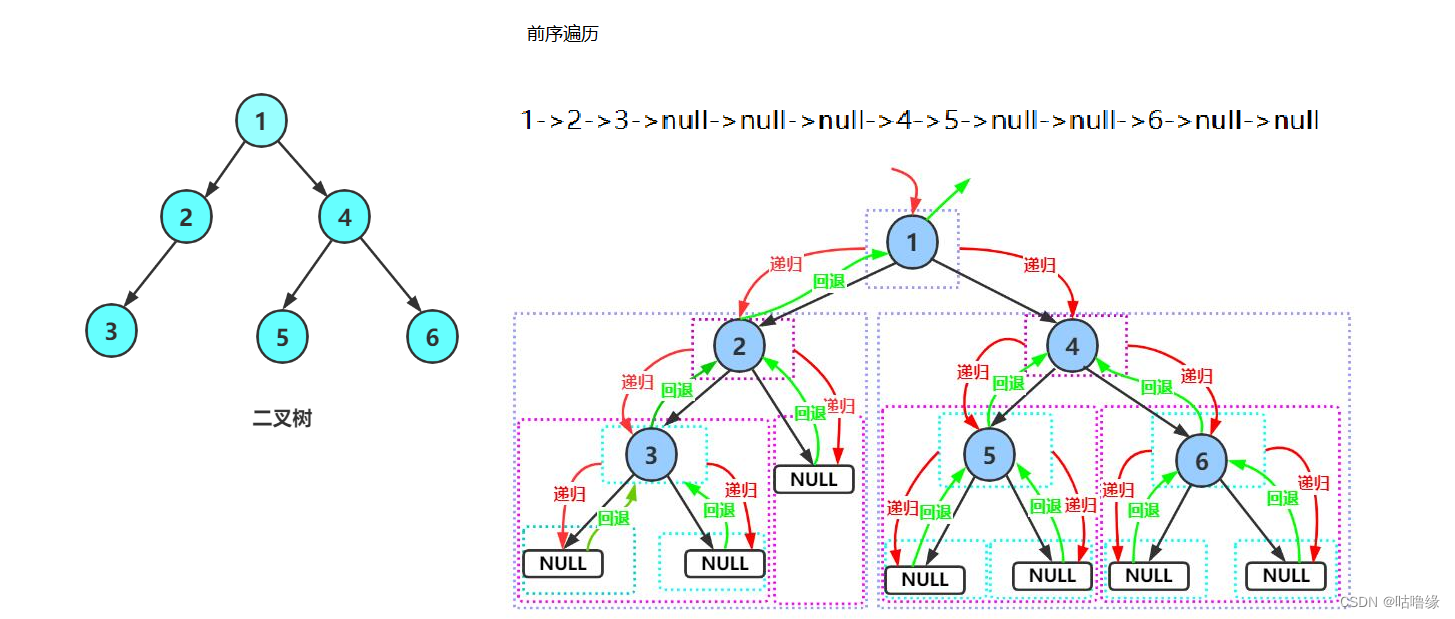
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历

前序遍历

如上图同理
中序遍历

后序遍历

1.2代码测试

前序代码

void PreOrder(BTNode* root)
{if (root == NULL){printf("NULL->");return;//这里的return很重要，我们需要回归到原来的函数接着执行下面的语句}printf("%d->", root->data);PreOrder(root->left);PreOrder(root->right);
}

这里printf(“%d->”, root->data);语句的摆放位置实际上就是前序中序后序的区别，我们采用递归来解决这个问题，当然这部分需要对函数栈帧的创建和销毁理解

#include<stdio.h>
#include<stdlib.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyBTNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail");}newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}
void PreOrder(BTNode* root)
{if (root == NULL){printf("NULL->");return;}printf("%d->", root->data);PreOrder(root->left);PreOrder(root->right);
}int main()
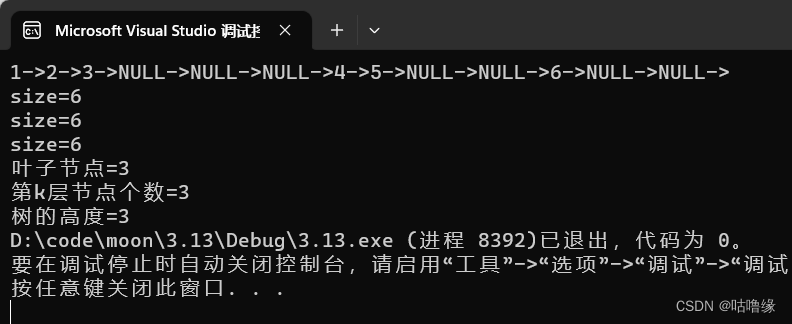
{BTNode* n1 = BuyBTNode(1);BTNode* n2 = BuyBTNode(2);BTNode* n3 = BuyBTNode(3);BTNode* n4 = BuyBTNode(4);BTNode* n5 = BuyBTNode(5);BTNode* n6 = BuyBTNode(6);n1->left = n2;n1->right = n4;n2->left = n3;n4->left = n5;n4->right = n6;PreOrder(n1);}

1.3层序遍历

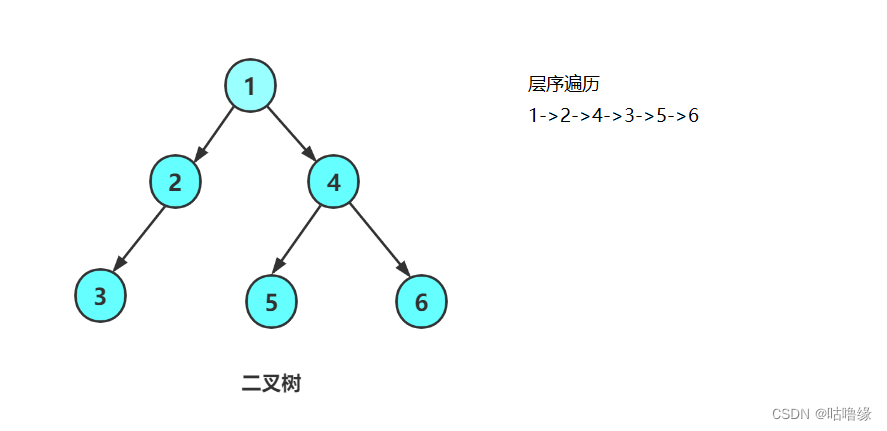
层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

1.4二叉树遍历习题

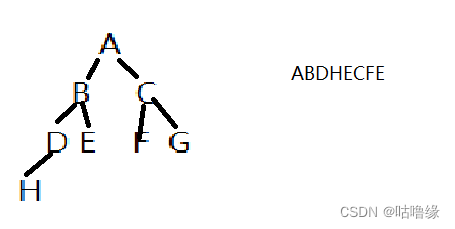
1.某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。该完全二叉树的前序序列为（ ）
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA

2.二叉树的先序遍历和中序遍历如下：先序遍历：EFHIGJK;中序遍历：HFIEJKG.则二叉树根结点为（）
A E
B F
C G
D H

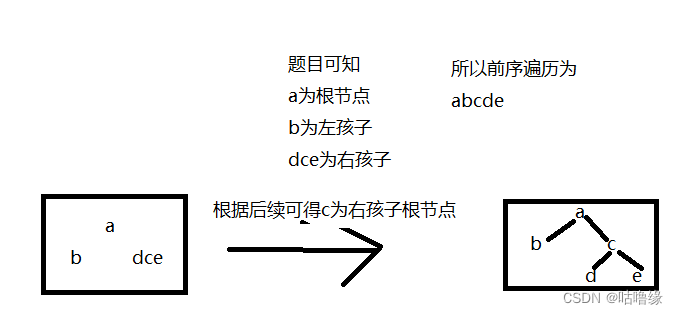
3.设一课二叉树的中序遍历序列：badce，后序遍历序列：bdeca，则二叉树前序遍历序列为____。
A adbce
B decab
C debac
D abcde

4.某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF ，则按层次输出（同一层从左到右）的序列
为
A FEDCBA
B CBAFED
C DEFCBA
D ABCDEF

2.节点个数以及高度

2.1二叉树节点个数

int BinaryTreeSize(BTNode* root)
{if (root == NULL){return;}int size = 0;size++;BinaryTreeSize(root->left);BinaryTreeSize(root->right);return size;
}

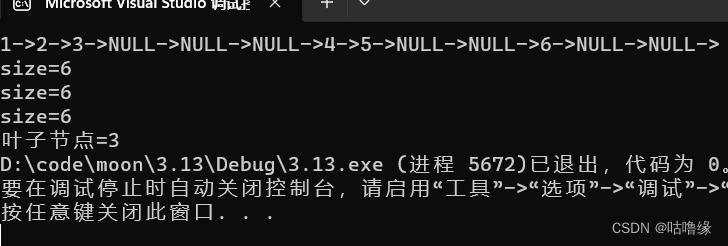
我们首先来看这段代码能成功计算出来吗？

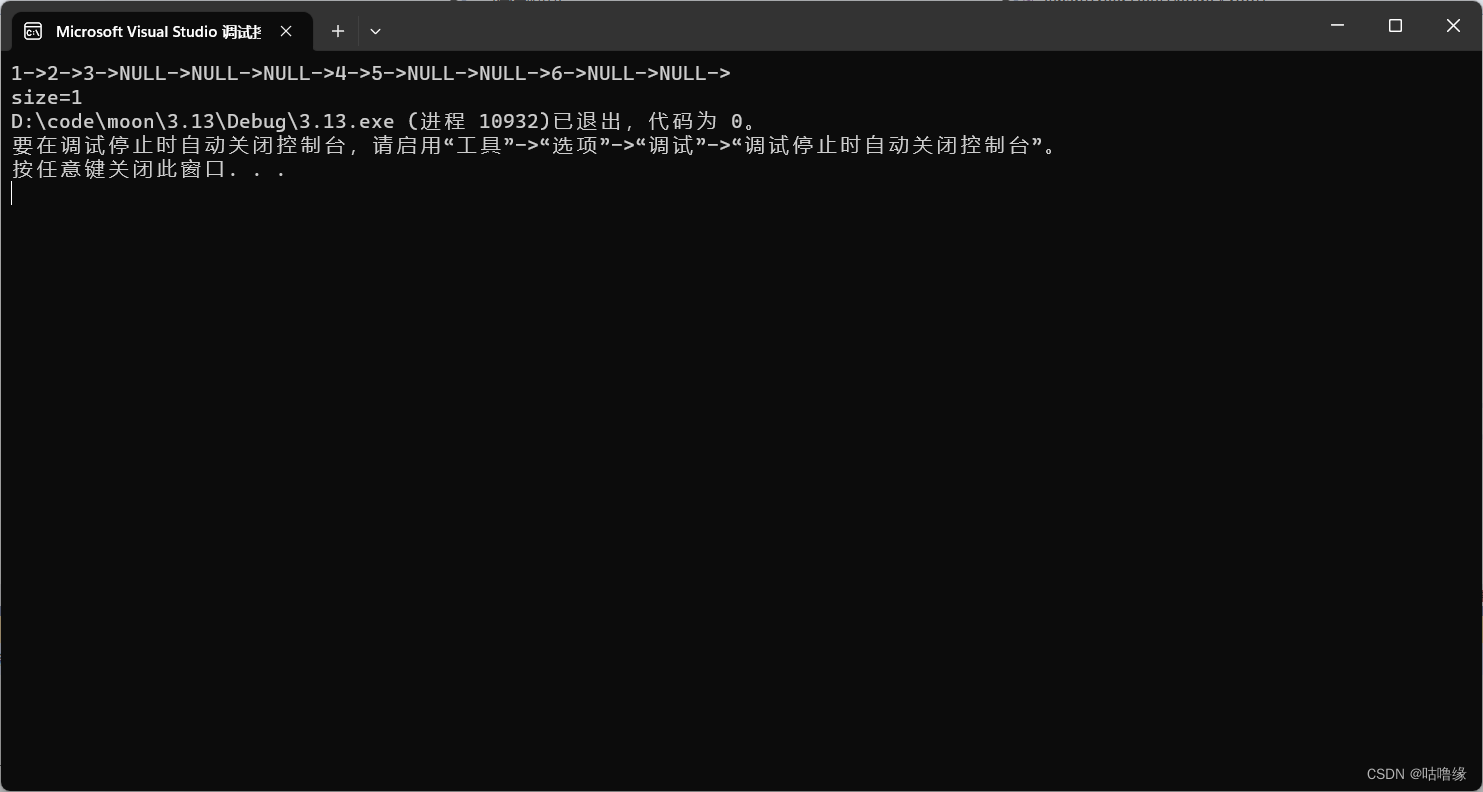
显然运行结果错误，因为函数栈帧创建时，每个size++，都不是加在一个size上，所以实际上只有第一次的++，起了效果，所以输出1

那我们修改size为静态变量

int BinaryTreeSize(BTNode* root)
{if (root == NULL){return;}static int size = 0;size++;BinaryTreeSize(root->left);BinaryTreeSize(root->right);return size;
}

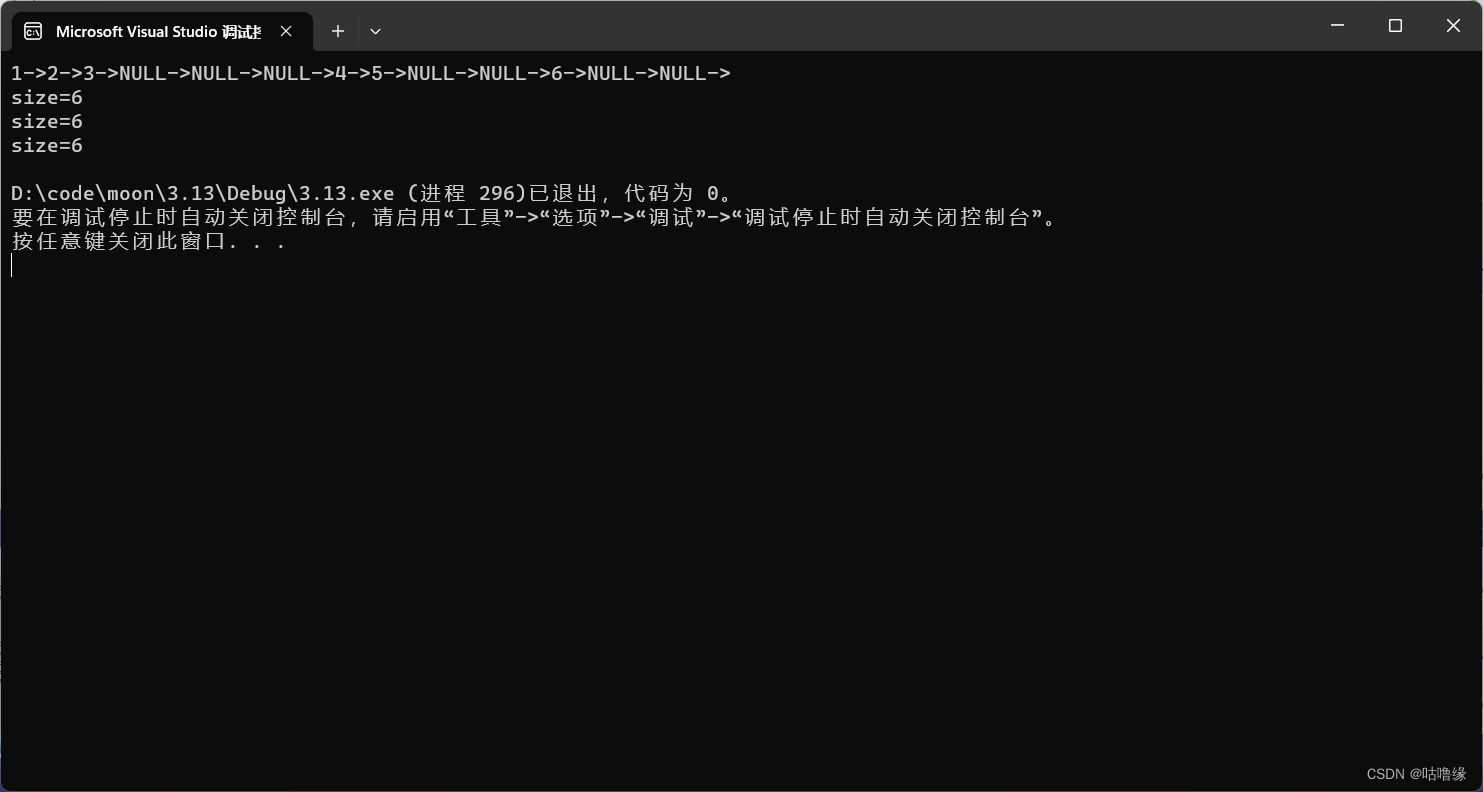
显然第一次结果是正确的，但是我们多运行几次发现，size每次都会加6，出现这种情况正因为他是静态变量，只经历一次初始化，所以这种方法也行不通

这是我们想到了全局变量

int size = 0;
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return;}size++;BinaryTreeSize(root->left);BinaryTreeSize(root->right);return size;
}
int main()
{BTNode* n1 = BuyBTNode(1);BTNode* n2 = BuyBTNode(2);BTNode* n3 = BuyBTNode(3);BTNode* n4 = BuyBTNode(4);BTNode* n5 = BuyBTNode(5);BTNode* n6 = BuyBTNode(6);n1->left = n2;n1->right = n4;n2->left = n3;n4->left = n5;n4->right = n6;PreOrder(n1);printf("\n");size = 0;printf("size=%d\n",BinaryTreeSize(n1));size = 0;printf("size=%d\n", BinaryTreeSize(n1));size = 0;printf("size=%d\n", BinaryTreeSize(n1));
}

最优解

return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;

2.2叶子节点个树

int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return(BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right));
}

2.3第k层节点个数

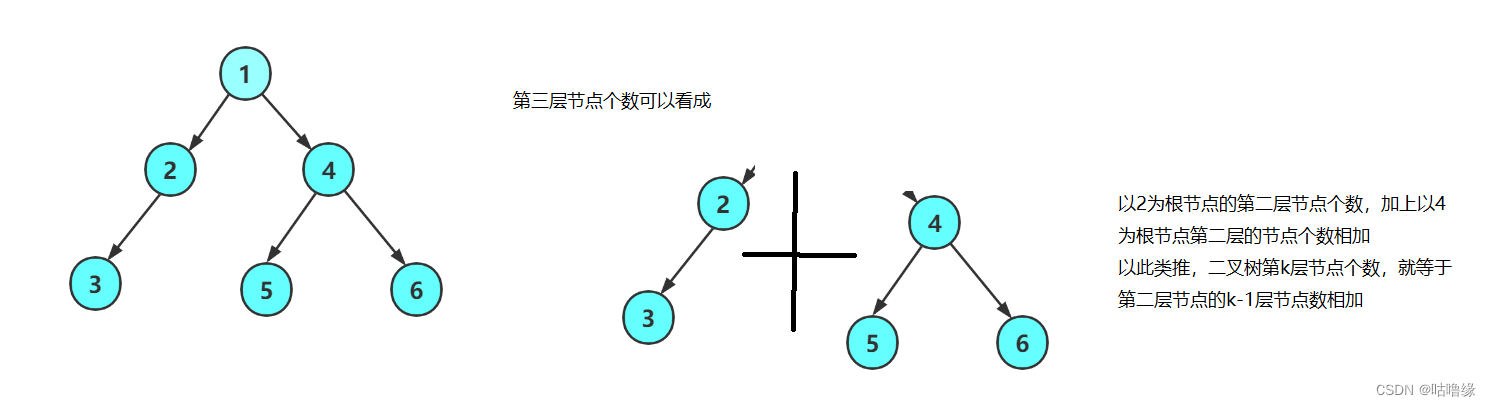
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

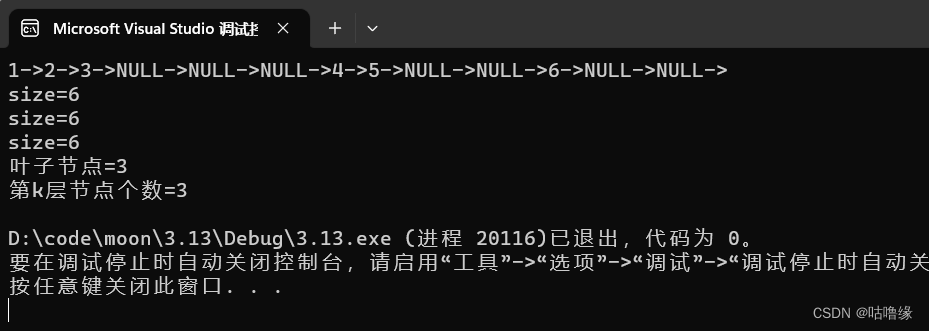
2.4树的高度

int TreeHeight(BTNode* root)
{if (root == NULL){return 0;}int leftHeight = TreeHeight(root->left);int RightHeight = TreeHeight(root->right);return leftHeight > RightHeight ? leftHeight + 1 : RightHeight + 1;
}