企业光纤局域网组网方案seo网络推广知识

目录

一 基本思想

二 代码实现 

三 非递归归并排序 

---

一 基本思想

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有 序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤

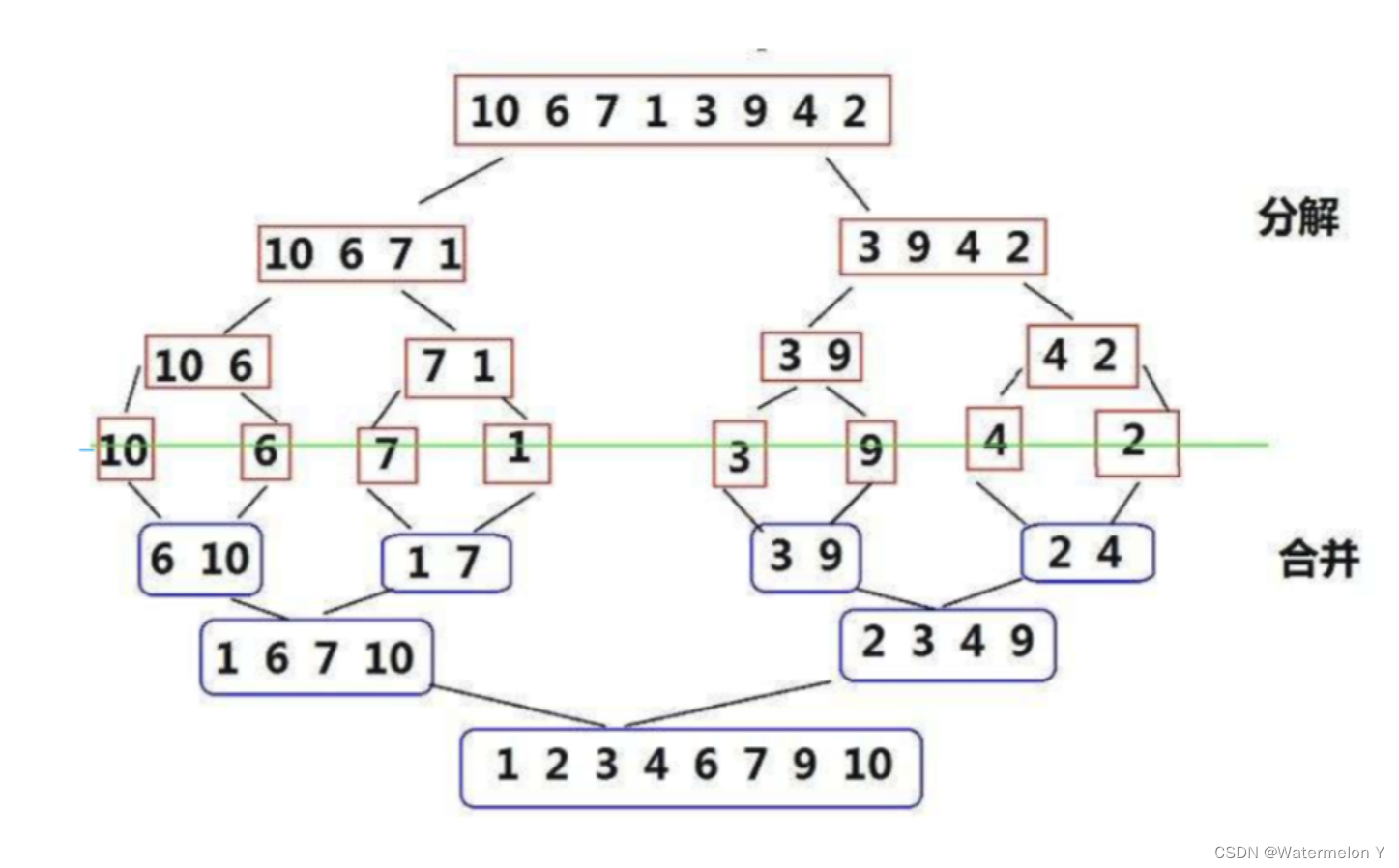
二 代码实现 

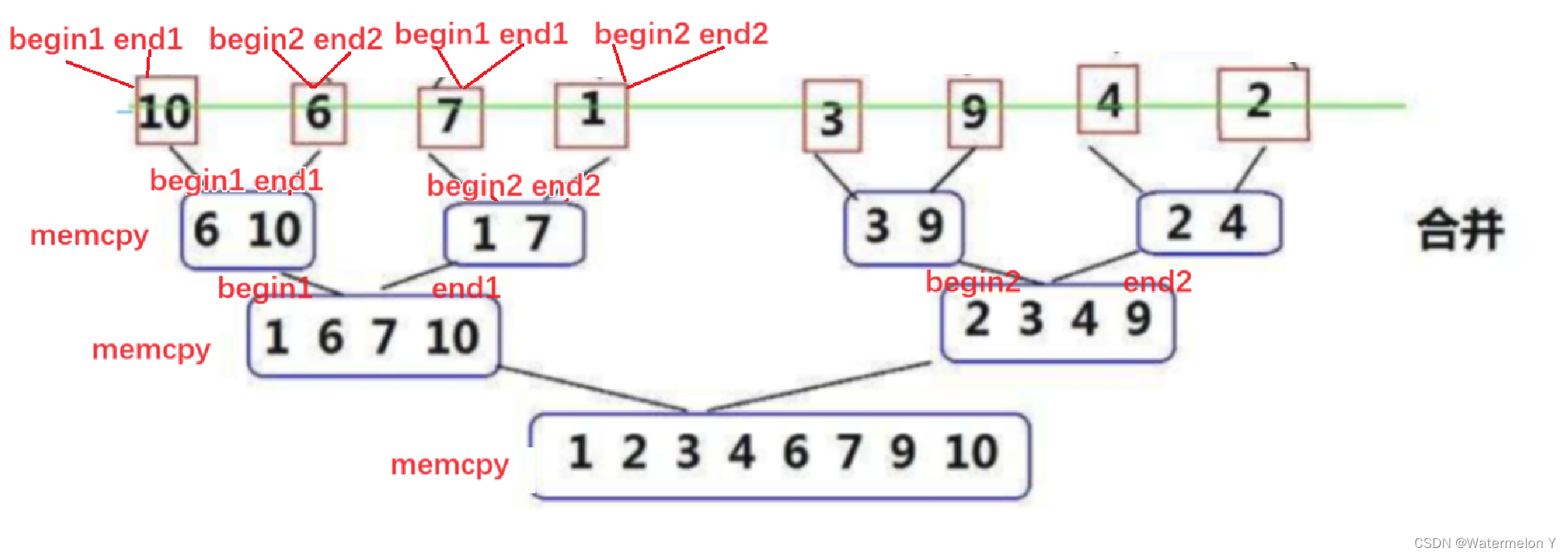
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>void _MergeSort(int* a, int* tmp, int begin, int end)
{if (begin >= end){return;}int mid = (begin + end) / 2;_MergeSort(a, tmp, begin, mid);_MergeSort(a, tmp, mid + 1, end);//归并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int index = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1)//如果[begin1, end1] 区间没有排完 接着排{tmp[index++] = a[begin1++];}while (begin2 <= end2)//如果[begin2, end2] 区间没有排完 接着排{tmp[index++] = a[begin2++];}memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));//拷贝回原数组
}void MergeSort(int* a, int n)
{int tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");exit(-1);}_MergeSort(a, tmp, 0, n-1);free(tmp);
}int main()
{int arr[] = { 10, 6, 7, 1, 3, 9, 4, 2 };MergeSort(arr, sizeof(arr) / sizeof(arr[0]));for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){printf("%d ", arr[i]);}return 0;
}

三 非递归归并排序 

void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");exit(-1);}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap-1;int begin2 = i + gap, end2 = i + 2 * gap - 1;if (begin2 >= n)//如果第二个区间 的begin2 已经超过了 就break 不用排这个区间了{break;}if (end2 >= n)//如果end2>= n 了 那就修正一下 最后一个数的下标就是n-1{end2 = n - 1;}int index = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));}gap *= 2;}free(tmp);
}
int main()
{int arr[] = { 10, 6, 7, 1, 3, 9, 4, 2 };MergeSortNonR(arr, sizeof(arr) / sizeof(arr[0]));for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){printf("%d ", arr[i]);}return 0;
}

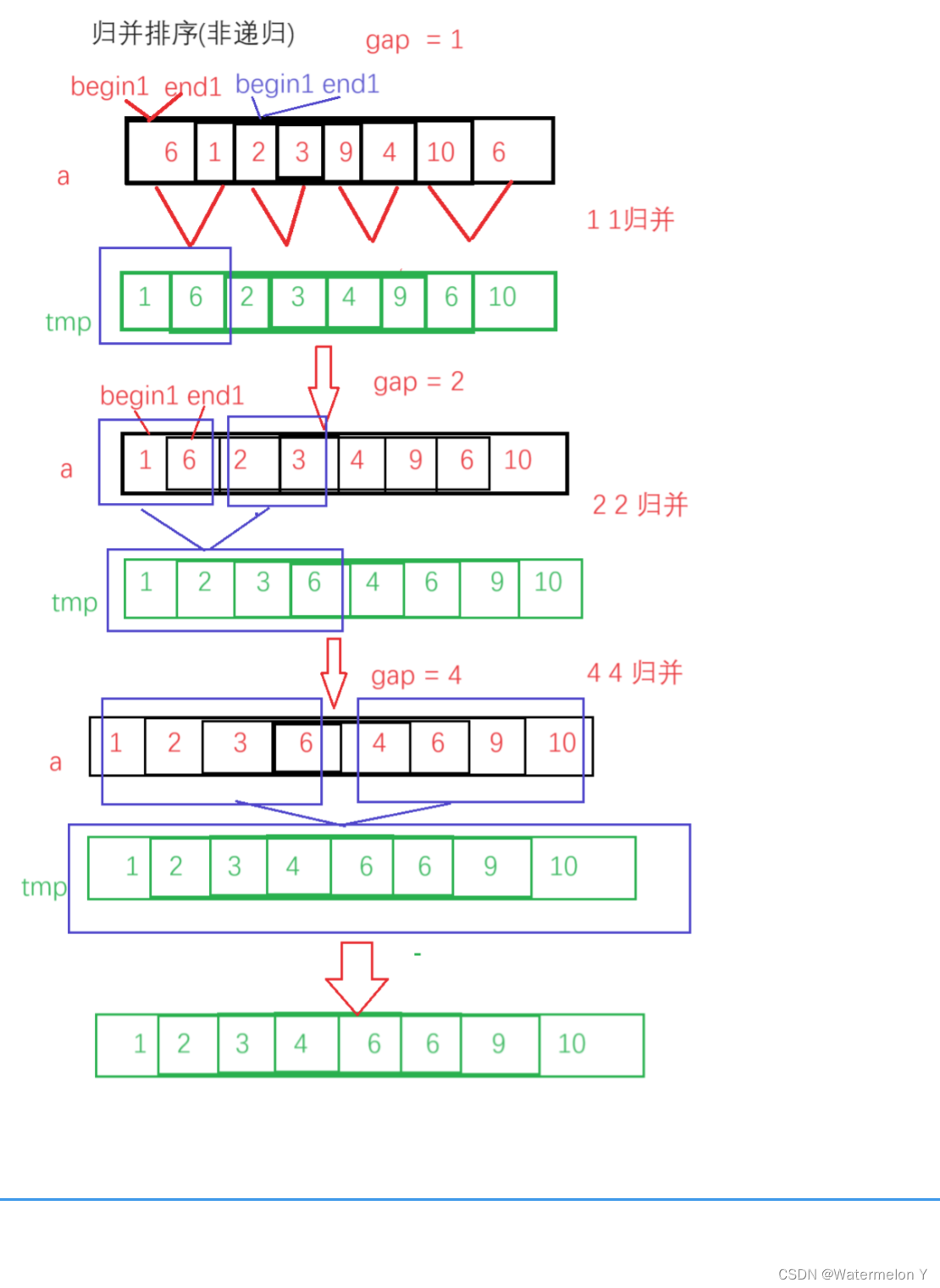
本节主要讲解了归并排序, 并且对递归和非递归版本进行了讲解,大家可以根据代码和图解进行理解, 归并排序并不难, 但是大家的二叉树的递归思想和基础必须要扎实(之前博客讲的有)

继续加油!