当前位置： 首页 > news >正文

乐清做网站的公司网站权重

news 2025/7/5 22:23:50
乐清做网站的公司,网站权重,上海城市建设大学网站,网站建设设计制目录 一、概念 二、实现 2.1 - BST.h 2.2 - test.cpp 三、应用 四、性能分析 一、概念 二叉搜索树（BST，Binary Search Tree），又称二叉排序树或二叉查找树。 二叉搜索树是一棵二叉树，可以为空；如果不…

目录

一、概念

二、实现

2.1 - BST.h

2.2 - test.cpp

三、应用

四、性能分析

 

一、概念

二叉搜索树（BST，Binary Search Tree），又称二叉排序树或二叉查找树。

二叉搜索树是一棵二叉树，可以为空；如果不为空，满足以下性质：

  • 非空左子树的所有键值小于其根节点的键值

  • 非空右子树的所有键值大于其根节点的键值

  • 左、右子树本身也都是二叉搜索树。

二、实现

2.1 - BST.h

#pragma once
​
#include <stack>
#include <iostream>
​
template<class K>
struct BSTNode
{BSTNode<K>* _left;BSTNode<K>* _right;K _key;
​BSTNode(const K& key = K()): _left(nullptr), _right(nullptr), _key(key){ }
};
​
template<class K>
class BST
{typedef BSTNode<K> BSTNode;
​
public:/*---------- 构造函数和析构函数 ----------*/// 默认构造函数BST() : _root(nullptr){ }
​// 拷贝构造函数（实现深拷贝）BST(const BST<K>& t){_root = Copy(t._root);}
​// 析构函数~BST(){Destroy(_root);}
​/*---------- 赋值运算符重载 ----------*/// 利用上面写好的拷贝构造函数实现深拷贝BST<K>& operator=(BST<K> tmp){std::swap(_root, tmp._root);return *this;}
​/*---------- 插入 ----------*/// 非递归写法bool Insert(const K& key){if (_root == nullptr){_root = new BSTNode(key);return true;}
​BSTNode* parent = nullptr;BSTNode* cur = _root;while (cur){parent = cur;if (key < cur->_key)cur = cur->_left;else if (key > cur->_key)cur = cur->_right;elsereturn false;}
​cur = new BSTNode(key);if (key < parent->_key)parent->_left = cur;elseparent->_right = cur;return true;}
​// 递归（Recursion）写法bool InsertRecursion(const K& key){return _InsertRecursion(_root, key);}
​/*---------- 删除 ----------*/// 非递归写法bool Erase(const K& key){BSTNode* parent = nullptr;BSTNode* cur = _root;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{if (cur->_left == nullptr)  // 左子树为空{if (parent == nullptr)  // 或者 cur == _root{_root = cur->_right;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}}else if (cur->_right == nullptr)  // 右子树为空{if (parent == nullptr)  // 或者 cur == _root{_root = cur->_left;}else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;}}else  // 左、右子树非空{// 找到左子树中关键字最大的节点（或者找到右子树中关键字最小的节点）BSTNode* parentLeftMax = cur;BSTNode* leftMax = cur->_left;while (leftMax->_right){parentLeftMax = leftMax;leftMax = leftMax->_right;}// 让 leftMax 指向的节点代替 cur 指向的节点，然后删除 leftMax 指向的节点，// 这样就转换成了上面的情况std::swap(cur->_key, leftMax->_key);if (parentLeftMax->_left == leftMax)  // 或者 parentLeftMax == curparentLeftMax->_left = leftMax->_left;elseparentLeftMax->_right = leftMax->_left;cur = leftMax;}delete cur;return true;}}return false;}
​// 递归写法bool EraseRecursion(const K& key){return _EraseRecursion(_root, key);}
​/*---------- 查找 ----------*/// 非递归写法bool Search(const K& key) const{BSTNode* cur = _root;while (cur){if (key < cur->_key)cur = cur->_left;else if (key > cur->_key)cur = cur->_right;elsereturn true;}return false;}
​// 递归写法bool SearchRecursion(const K& key) const{return _SearchRecursion(_root, key);}
​/*---------- 中序遍历 ----------*/// 非递归写法void InOrder() const{std::stack<BSTNode*> st;BSTNode* cur = _root;while (cur || !st.empty()){while (cur){st.push(cur);cur = cur->_left;}BSTNode* top = st.top();st.pop();std::cout << top->_key << " ";cur = top->_right;}std::cout << std::endl;}
​// 递归写法void InOrderRecursion() const{_InOrderRecursion(_root);std::cout << std::endl;}
​
private:BSTNode* Copy(BSTNode* root){if (root == nullptr)return nullptr;
​BSTNode* copyRoot = new BSTNode(root->_key);copyRoot->_left = Copy(root->_left);copyRoot->_right = Copy(root->_right);return copyRoot;}
​void Destroy(BSTNode*& root){// 【注意：root 为 _root 或者某个节点的左或右指针的引用】if (root == nullptr)return;
​Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}
​bool _InsertRecursion(BSTNode*& root, const K& key){// 【注意：root 为 _root 或者某个节点的左或右指针的引用】if (root == nullptr){root = new BSTNode(key);return true;}
​if (key < root->_key)_InsertRecursion(root->_left, key);else if (key > root->_key)_InsertRecursion(root->_right, key);elsereturn false;}
​bool _EraseRecursion(BSTNode*& root, const K& key){// 【注意：root 为 _root 或者某个节点的左或右指针的引用】if (root == nullptr)return false;
​if (key < root->_key)_EraseRecursion(root->_left, key);else if (key > root->_key)_EraseRecursion(root->_right, key);else{BSTNode* tmp = root;if (root->_left == nullptr)root = root->_right;else if (root->_right == nullptr)root = root->_left;else{BSTNode* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}std::swap(leftMax->_key, root->_key);return _EraseRecursion(root->_left, key);}delete tmp;return true;}}
​bool _SearchRecursion(BSTNode* root, const K& key) const{if (root == nullptr)return false;
​if (key < root->_key)_SearchRecursion(root->_left, key);else if (key > root->_key)_SearchRecursion(root->_right, key);elsereturn true;}
​void _InOrderRecursion(BSTNode* root) const{if (root == nullptr)return;
​_InOrderRecursion(root->_left);std::cout << root->_key << " ";_InOrderRecursion(root->_right);}
​
private:BSTNode* _root;
};

2.2 - test.cpp

#include "BST.h"
using namespace std;
​
void TestBST1()
{int arr[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };BST<int> t1;for (auto e : arr){t1.Insert(e);}t1.InOrder();  // 1 3 4 6 7 8 10 13 14
​BST<int> t2(t1);t2.InOrder();  // 1 3 4 6 7 8 10 13 14
​BST<int> t3;t3 = t1;t1.InOrder();  // 1 3 4 6 7 8 10 13 14
​// 左子树为空t1.Erase(4);t1.InOrder();  // 1 3 6 7 8 10 13 14t1.Erase(6);t1.InOrder();  // 1 3 7 8 10 13 14// 右子树为空t1.Erase(14);t1.InOrder();  // 1 3 7 8 10 13// 左、右子树非空t1.Erase(8);t1.InOrder();  // 1 3 7 10 13
​cout << t1.Search(8) << endl;  // 0cout << t1.Search(7) << endl;  // 1
}
​
void TestBST2()
{int arr[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };BST<int> t;for (auto e : arr){t.InsertRecursion(e);}t.InOrderRecursion();  // 1 3 4 6 7 8 10 13 14
​// 左子树为空t.EraseRecursion(4);t.InOrderRecursion();  // 1 3 6 7 8 10 13 14t.EraseRecursion(6);t.InOrderRecursion();  // 1 3 7 8 10 13 14// 右子树为空t.EraseRecursion(14);t.InOrderRecursion();  // 1 3 7 8 10 13// 左、右子树非空t.EraseRecursion(8);t.InOrderRecursion();  // 1 3 7 10 13
​cout << t.SearchRecursion(8) << endl;  // 0cout << t.SearchRecursion(7) << endl;  // 1
}
​
int main()
{TestBST1();TestBST2();return 0;
}

 

三、应用

  1. K 模型：结构体中只需要存储关键码 key，关键码即为需要搜索到的值。

    例如，要判断一个单词是否拼写正确，我们首先把词库中的每个单词作为 key，构建一棵二叉搜索树，然后在这棵二叉搜索树中检索单词是否存在，若存在则表明拼写正确，不存在则表明拼写错误。

  2. KV 模型：每个关键码 key，都有与之对应的值 value，即 <key, value> 的键值对。

    这种模型在现实生活中也很常见：

    • 比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文 <word, Chinese> 就构成一种键值对。

    • 再比如统计单词次数，统计成功后，给定单词就可以快速找到其出现的次数，单词与其出现的次数 <word, count> 就构成一种键值对。

    BST.h：

    #pragma once
​
#include <iostream>
​
template<class K, class V>
struct BSTNode
{BSTNode<K, V>* _left;BSTNode<K, V>* _right;K _key;V _value;
​BSTNode(const K& key = K(), const V& value = V()): _left(nullptr), _right(nullptr), _key(key), _value(value){ }
};
​
template<class K, class V>
class BST
{typedef BSTNode<K, V> BSTNode;
​
public:BST() : _root(nullptr){ }
​BST(const BST<K, V>& t){_root = Copy(t._root);}
​~BST(){Destroy(_root);}
​BST<K, V>& operator=(BST<K, V> tmp){std::swap(_root, tmp._root);return *this;}
​bool Insert(const K& key, const V& value){return _Insert(_root, key, value);}
​bool Erase(const K& key){return _Erase(_root, key);}
​BSTNode* Search(const K& key) const{return _Search(_root, key);}
​void InOrder() const{_InOrder(_root);std::cout << std::endl;}
​
private:BSTNode* Copy(BSTNode* root){if (root == nullptr)return nullptr;
​BSTNode* copyRoot = new BSTNode(root->_key, root->_value);copyRoot->_left = Copy(root->_left);copyRoot->_right = Copy(root->_right);return copyRoot;}
​void Destroy(BSTNode*& root){// 【注意：root 为 _root 或者某个节点的左或右指针的引用】if (root == nullptr)return;
​Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}
​bool _Insert(BSTNode*& root, const K& key, const V& value){// 【注意：root 为 _root 或者某个节点的左或右指针的引用】if (root == nullptr){root = new BSTNode(key, value);return true;}
​if (key < root->_key)_Insert(root->_left, key, value);else if (key > root->_key)_Insert(root->_right, key, value);elsereturn false;}
​bool _Erase(BSTNode*& root, const K& key){// 【注意：root 为 _root 或者某个节点的左或右指针的引用】if (root == nullptr)return false;
​if (key < root->_key)_Erase(root->_left, key);else if (key > root->_key)_Erase(root->_right, key);else{BSTNode* tmp = root;if (root->_left == nullptr)root = root->_right;else if (root->_right == nullptr)root = root->_left;else{BSTNode* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}std::swap(leftMax->_key, root->_key);return _Erase(root->_left, key);}delete tmp;return true;}}
​BSTNode* _Search(BSTNode* root, const K& key) const{if (root == nullptr)return nullptr;
​if (key < root->_key)_Search(root->_left, key);else if (key > root->_key)_Search(root->_right, key);elsereturn root;}
​void _InOrder(BSTNode* root) const{if (root == nullptr)return;
​_InOrder(root->_left);std::cout << root->_key << " : " << root->_value << std::endl;_InOrder(root->_right);}
private:BSTNode* _root;
};

    test.cpp：

    #include "BST_KV.h"
using namespace std;
​
void TestBST1()
{BST<string, string> t;t.Insert("insert", "插入");t.Insert("erase", "删除");t.Insert("search", "查找");t.Insert("left", "左边");t.Insert("right", "右边");// 输入英文单词，找到对应的中文string str;while (cin >> str){BSTNode<string, string>* ret = t.Search(str);if (ret)cout << str << "对应的中文是：" << ret->_value << endl;elsecout << "单词拼写错误，词库中没有此单词！" << endl;}
}
​
void TestBST2()
{string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };BST<string, int> t;// 统计每种水果出现的次数for (const auto& str : arr){BSTNode<string, int>* ret = t.Search(str);if (ret == nullptr)t.Insert(str, 1);elseret->_value += 1;}t.InOrder();// 苹果 : 6// 西瓜: 3// 香蕉 : 2
}
​
int main()
{// TestBST1();TestBST2();return 0;
}

四、性能分析

在二叉搜索树的插入和删除操作中，都必须先进行查找操作，所以查找的效率就代表了各个操作的性能。

对含 n 个节点的二叉搜索树，若每个节点查找的概率相等，则二叉搜树的平均查找长度是节点在二叉搜树树的深度的函数，即节点越深，比较次数越多。

但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树，例如：

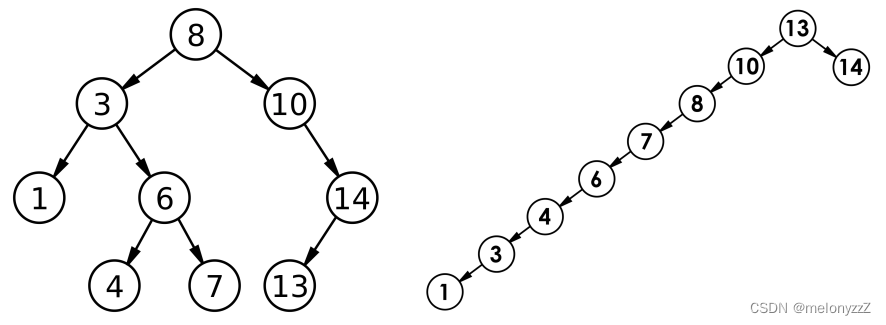
最好情况下，二叉搜索树为完全二叉树（或者接近完全二叉树），其平均比较次数为 ​。

最坏情况下，二叉搜索树退化为单支树（或者类似单支树），其平均比较次数为 。

如果退化成单支树，二叉搜树的性能就丢失了，那么能否改进，不论按照什么次序插入关键码，二叉搜索树的性能都能达到最优？

后续所要学习的 AVL 树和红黑树就可以解决上述问题。

http://www.dinnco.com/news/23855.html

相关文章：

  • 网页设计个人简历怎么做厦门seo关键词排名
  • 哪个网站做化妆品效果好学技术的培训学校
  • wordpress flask上海网站seoseodian
  • 企点qq是什么seo网站排名优化教程
  • 做网站3年3万营销型网站设计
  • 企业集团网站建设与运营管理培训
  • 网站模版超市自助建站申请
  • 做驾校题目用什么网站好百度搜索引擎的使用方法
  • 陕西 做网站的公司百度免费推广怎么做
  • 做网站为什么赚钱苏州优化排名seo
  • 网站建设合同.doc全国广告投放平台
  • html简单网站开发案例市场推广的方法和规划
  • 哪些企业需要做网站免费推广方式都有哪些
  • 官方网站建设审批手续怎么快速排名
  • 做影视网站挣钱吗抖音营销软件
  • 专业的网站建设制作服务沈阳seo网站关键词优化
  • 动画形式的h5在哪个网站做中国进入全国紧急状态
  • 网站开发存在的问题友情链接查询结果
  • 品牌网站建设 意义企业官网定制设计
  • 唯品会网站开发技术分析软件公司
  • 微信怎么做一些微网站市场营销手段有哪四种
  • 医院网站设计怎么做北京seo公司工作
  • 做网站的的价格一份完整app运营推广方案
  • 海外营销是做什么的seo方法培训
  • 如何开网店详细教程广州aso优化
  • 西安网站建设费用百度新站关键词排名
  • 网站怎样做才能有点击率免费发布活动的平台
  • 网站栏目建设图深圳网站搜索优化工具
  • 网站是哪个公司做的好怎么样把广告做在百度上
  • php做网站用什么开发工具网站如何快速推广