用dw做购票网站模板澳门seo关键词排名

红黑树

• 前提：二叉搜索树（左 < 根 < 右）—— 左根右
• 根和**叶子（NULL）**都是黑色 —— 根叶黑
• 不存在连续的两个红色节点 —— 不红红
• 任一结点到叶所有路径黑结点数量相同 —— 黑路同

注意：叶子节点是空结点
原因：空结点可以帮助捋清所有路径，确保所有路径黑色结点数量都相同

• 最长路径不超过最短路径的两倍（任一结点左右子树高度相差不超过两倍）
  • AVL树（平衡二叉树）左右子树高度绝对值不超过1，可发现 AVL 树对平衡要求更加严格，在树高上比红黑树控制得更加平衡 —— 查询上，红黑树略逊于 AVL 树，但时间复杂度都是O(logn)
  • 但红黑树在插入和删除上更高效

红黑树插入时的调整？

红黑树插入结点默认是红色，且只可能违反根叶红或者不红红

若插入时，红黑树性质被破坏，需要根据以下几种情况来进行调整：

1. 插入结点是根结点

• 根结点直接变黑（违反根叶黑的性质）

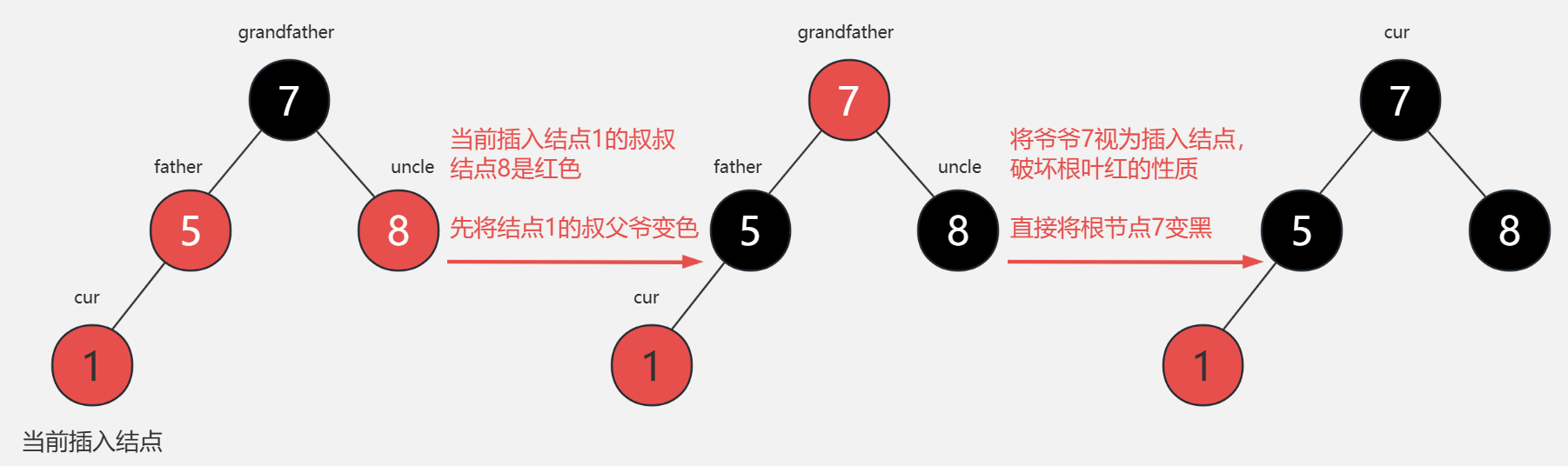
2. 插入结点的叔叔是红色

• 叔父爷变色（红变黑，黑变红），爷爷变插入节点（将爷爷视为插入结点，继续判定是否破坏红黑树的性质）
  

3. 插入结点的叔叔是黑色

• 根据（LL、RR、LR、RL）以爷爷作为旋转点进行旋转，然后对旋转点和旋转中心变色
  • 关于（LL、RR、LR、RL）是平衡二叉树的旋转操作，可看文章：【数据结构 | 平衡二叉树】失衡时如何调整
    也可以看视频讲解：平衡二叉树(AVL树)

LL 型

RR型

LR型

RL型

对上述过程有疑问，可以看这个视频来理解：红黑树 - 定义, 插入, 构建