当前位置：首页 > news >正文

义乌网站建设排名seo怎么样

news 2025/7/16 16:34:46

义乌网站建设,排名seo怎么样,京东app下载官网免费下载,建设通查询目录一、什么是贪心？ （一）以教室调度问题为例 1. 问题 2. 具体做法如下 3. 因此将在这间教室上如下三堂课 4. 结论 （二）贪心算法介绍 1. 贪心算法一般解题步骤二、最优装载问题 （一&#xf…

一、什么是贪心？

（一）以教室调度问题为例

1. 问题

2. 具体做法如下

3. 因此将在这间教室上如下三堂课

4. 结论

（二）贪心算法介绍

1. 贪心算法一般解题步骤

二、最优装载问题

（一）问题

（二）分析

（三）核心代码

（四）完整代码

三、完全背包问题

（一）问题

（二）分析

（三）举例

（四）核心代码

（五）完整代码

（六）物品类的完整代码

一、什么是贪心？

（一）以教室调度问题为例

1. 问题

假设有如下课程表，你希望将尽可能多的课程安排在某一间教室上

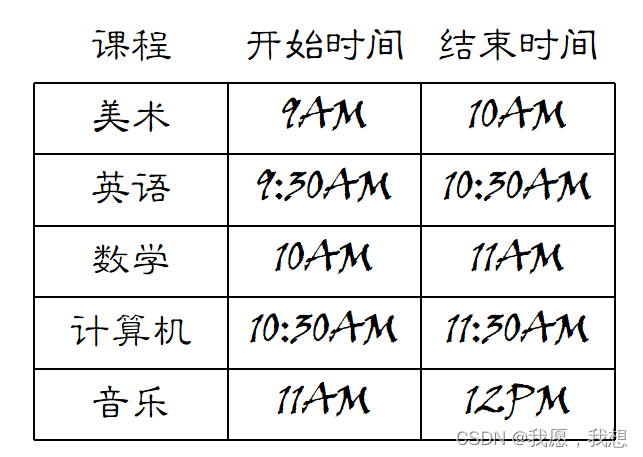
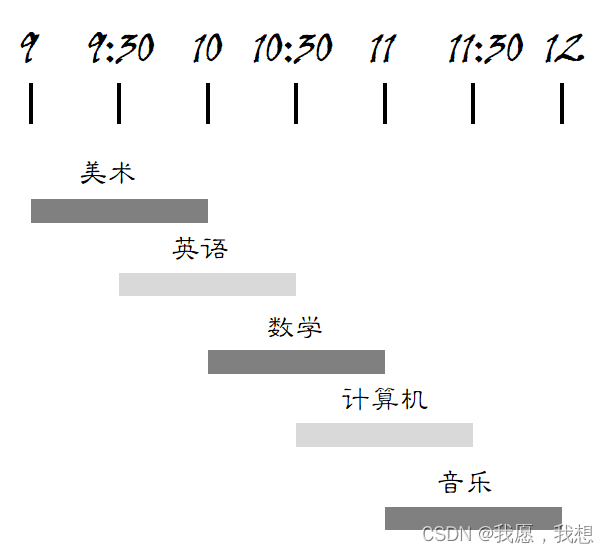
2. 具体做法如下

第一步：选出结束最早的课，它就是要在这间教室上的第一堂课
第二步：接下来，必须选择第一堂课结束后才开始的课。同样，选择开始最早的课，这将是要在这间教室上的第二堂课

3. 因此将在这间教室上如下三堂课

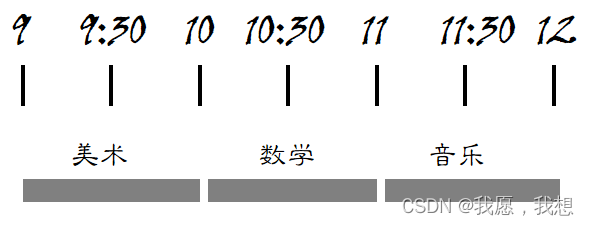
4. 结论

这道题就采取的贪心算法===>每步都采取最优的做法

（二）贪心算法介绍

贪心算法又称贪婪算法，是指在对问题求解时，总是做出当前看来最好的选择，它不是从整体上加以考虑，所做出的仅是在某种意义上的局部最优解。而局部的最优解叠加在一起便是该问题整体的最优解，或者近似最优解。

1. 贪心算法一般解题步骤

将问题分解为若干个子问题
找出合适的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解

二、最优装载问题

（一）问题

有一艘海盗船，载重量为C，每一件古董的重量为 $w_{i}$ ，海盗们如何尽可能的把多数量的宝贝装上海盗船？

（二）分析

当载重量为定值的时候， $w_{i}$ 越小时，可装载的古董数量n越大，只要依次选择最小重量的古董即可
把n个古董的重量从小到大（非递减）排序，然后根据贪心策略尽可能多地选出前i个古董，直到不能继续装为止

（三）核心代码

template<typename T1,typename T2,typename T3>
void Loading(T1 c, vector<T2>& w, vector<T3>& t, vector<bool>& v)
{//冒泡排序for (int i = w.size() - 1; i > 0; i--)//扫描次数{for (int j = 0; j < i; j++){if (w[j] > w[j + 1]){swap(w[j], w[j + 1]);//交换物品重量swap(t[j], t[j + 1]);//交换物品的序号}}}for (int k = 0; w[k] <= c; k++){v[k] = true;c = c - w[k];//船的剩余装载量}
}

（四）完整代码

#include<iostream>
#include<vector>
#include<stdbool.h>
using namespace std;
template<typename T1,typename T2,typename T3>
void Loading(T1 c, vector<T2>& w, vector<T3>& t, vector<bool>& v)
{//冒泡排序for (int i = w.size() - 1; i > 0; i--)//扫描次数{for (int j = 0; j < i; j++){if (w[j] > w[j + 1]){swap(w[j], w[j + 1]);//交换物品重量swap(t[j], t[j + 1]);//交换物品的序号}}}for (int k = 0; w[k] <= c; k++){v[k] = true;c = c - w[k];//船的剩余装载量}
}
int main()
{float c;//表示船的最大载重和物品个数int n;//物品个数cout << "请依次输入船的最大载重和物品个数：" << endl;cin >> c >> n;vector<float> w(n);//存放物品的重量vector<int> t(n);;//存放物品的下标vector<bool> v(n);//记录物品是否装入船中cout << "请依次输入物品重量：" << endl;for (int i = 0; i < n; i++)//初始化物品信息{cin >> w[i];t[i] = i;v[i] = false;}Loading(c,w,t,v);cout << "装入了：" << endl;for (int i = 0; i < w.size(); i++)//输出装入的物品{if (v[i] == true)cout << t[i] << "号物品，" << "重量为：" << w[i] << endl;}return 0;
}
//测试数据
//30 8
//4 10.5 7.8 4.9 5.1 3.3 4.6 3.2//结果
//装入了：
//7号物品，重量为：3.2
//5号物品，重量为：3.3
//0号物品，重量为：4
//6号物品，重量为：4.6
//3号物品，重量为：4.9
//4号物品，重量为：5.1

三、完全背包问题

（一）问题

有n件物品，每件物品有一定的重量w和相应的价值v，背包的最大容量为bagW，一种物品只能拿一样（不可重复拿），物品可以分割，求解将哪些物品装入背包里物品价值总和最大？

（二）分析

依照贪心策略，每次选取单位重量价值最大的物品，也就是说每次选择性价比（价值/重量）最高的物品，如果达到运载重量bagW，那么一定能得到价值最大

（三）举例

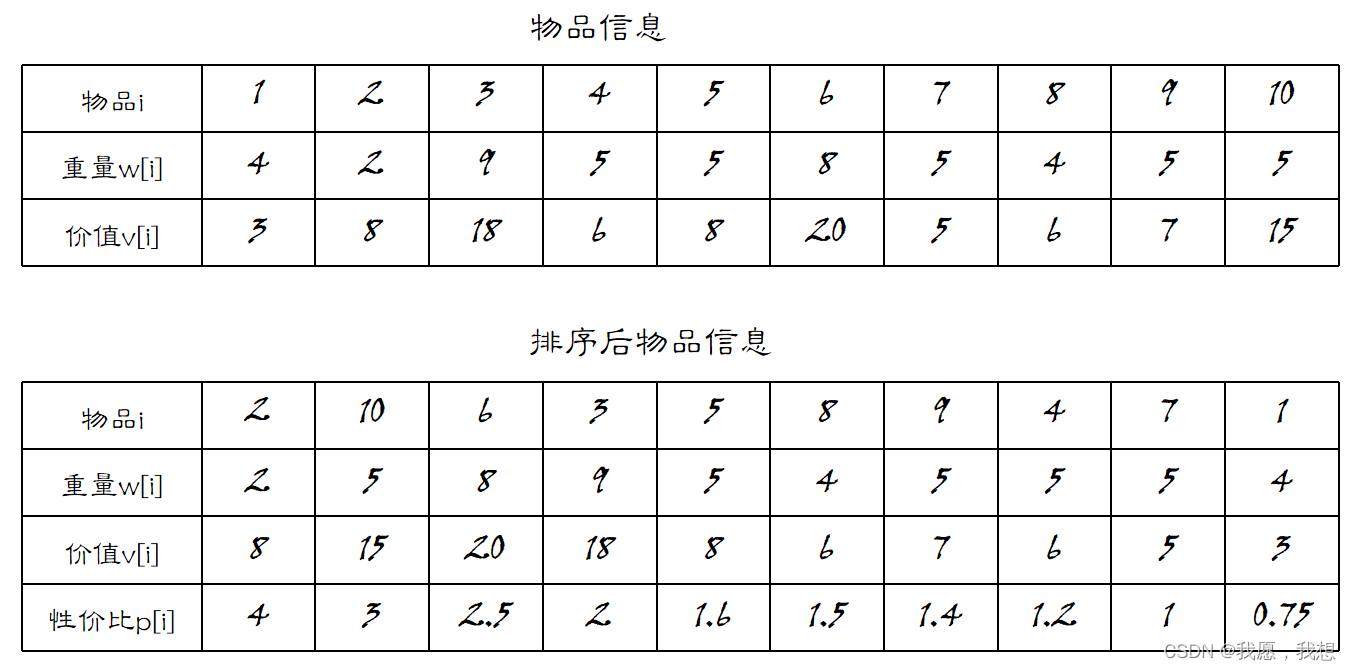
背包最大容量为30，在依次选择物品2、10、6、3、5后，背包最大价值达到69，背包剩余容量为 $30-(2+5+8+9+5)=1$ ，只能装8号物品的 $\frac{1}{4}$ ，此时背包最大价值为 $69+\frac{1}{4}\times 6=70.5$

（四）核心代码

void CompletePack(int _bagW,int n,struct goods*ps)
{double sum = 0;//背包总价值for (int i = 0;i<n; i++){if (_bagW >ps[i].w)//背包容量大于物品重量{ps[i].c = 1;sum =sum+ ps[i].v;_bagW = _bagW - ps[i].w;//剩余背包容量}else//背包容量小于物品重量{ps[i].c = (double)_bagW / (double)ps[i].w;//装入物品的比例（必须要强制转换）sum =sum+ps[i].c *ps[i].v;break;}}cout << "背包最大价值：" << sum << endl;
}

（五）完整代码

#include<iostream>
#include<algorithm>
#include<iomanip>//setw的头文件
using namespace std;
#define MAX 100//物品数量最多为100
struct goods
{int n;//物品编号int w;//物品重量int v;//物品价值double p;//物品性价比double c;//记录装入物品的比例（如果物品完全放入背包，则c=1；不放入,c=0）
}g[MAX];void Init(int n, struct goods*ps);//初始化物品信息
bool cmp(struct goods a,struct goods b);//比较
void CompletePack(int _bagW,int n,struct goods*ps);
void print(int n, struct goods* ps);//遍历void Init(int n, struct goods*ps)//初始化物品信息
{cout << "请依次输入物品的重量和价值：" << endl;for (int i = 0; i < n; i++){ps[i].n = i;//物品编号cin >>ps[i].w >> ps[i].v;//初始化物品重量和价值ps[i].p = (double)ps[i].v / (double)ps[i].w;//性价比ps[i].c = 0;//都没有放入背包}
}bool cmp(struct goods a,struct goods b)//比较
{return a.p > b.p;//根据物品单位价值从大到小排序
}
void CompletePack(int _bagW,int n,struct goods*ps)
{double sum = 0;//背包总价值for (int i = 0;i<n; i++){if (_bagW >ps[i].w)//背包容量大于物品重量{ps[i].c = 1;sum =sum+ ps[i].v;_bagW = _bagW - ps[i].w;//剩余背包容量}else//背包容量小于物品重量{ps[i].c = (double)_bagW / (double)ps[i].w;//装入物品的比例（必须要强制转换）sum =sum+ps[i].c *ps[i].v;break;}}cout << "背包最大价值：" << sum << endl;
}
void print(int n, struct goods* ps)
{for (int i = 0; i < n; i++){if (ps[i].c != 0){if (ps[i].c == 1)cout << "物品" << ps[i].n << setw(20) << "价值为：" << ps[i].v << endl;elsecout << "物品" << ps[i].n << "装入了" << ps[i].c <<setw(8)<< "   价值为：" << ps[i].v << endl;}}
}int main()
{int bagW, n;//背包最大容量和物品数量cout << "请依次输入物品重量和物品数量：" << endl;cin >> bagW >> n;Init(n,g);//初始化物品信息cout << endl<<endl ;sort(g, g + n, cmp);//排序CompletePack(bagW,n, g);print(n, g);return 0;
}//测试数据
// 背包容量30  物品数量10
//4 3
//2 8
//9 18
//5 6
//5 8
//8 20
//5 5
//4 6
//5 7
//5 15//结果
//背包最大价值：70.5
//物品1            价值为：8
//物品9            价值为：15
//物品5            价值为：20
//物品2            价值为：18
//物品4            价值为：8
//物品7装入了0.25   价值为：6

（六）物品类的完整代码

#include<iostream>
#include <iomanip>//setw的头文件
using namespace std;
#define MAX 20//物品数量最多为20
class goods
{
private:int number;//物品编号int weight;//物品重量double value;//物品价值double percentage;//物品性价比double choice;//记录装入物品的比例（如果物品完全放入背包，则choice=1；不放入,choice=0）
public:goods() { ; }goods(int _n,int _w, double _v, double _p, double _c)//构造函数{this->number = _n;this->weight = _w;this->value = _v;this->percentage = _p;this->choice = _c;}//~goods();//析构函数//获取私有成员int getn();//获取私有成员numberint getw();//获取私有成员weightdouble getv();//获取私有成员valuedouble getp();//获取私有成员percentagedouble getc();//获取私有成员choice//修改私有成员void setn(int _n);//修改私有成员的numbervoid setw(int _w);void setv(double _v);void setp(double _p);void setc(double _c);
};int goods::getn()
{return number;
}
int goods::getw()//获取私有成员weight
{return weight;
}
double goods::getv()
{return value;
}
double goods::getp()
{return percentage;
}
double goods::getc()
{return choice;
}void goods::setn(int _n)
{number = _n;
}
void goods::setw(int _w)
{weight = _w;
}
void goods::setv(double _v)
{value = _v;
}
void goods::setp(double _p)
{percentage = _p;
}
void goods::setc(double _c)
{choice = _c;
}
int main()
{int bagW, n;//背包最大容量和物品数量cout << "请依次输入背包容量和物品数量：" << endl;cin >> bagW >> n;//goods *g=new goods[MAX];goods g[MAX];cout << "请依次输入物品重量和物品价值：" << endl;for (int i = 0; i < n; i++){int _n,_w,_c;//物品编号，物品重量，物品是否放入了背包double _v, _p;//物品价值，物品性价比cin >> _w >> _v;_p = _v / _w;//性价比_n = i;//编号_c = 0;//是否放入了背包goods gg(_n, _w, _v, _p, _c);g[i] = gg;}for (int i = 0; i <= n - 1; i++)//简单选择排序（按照性价比从大到小）{double max = g[i].getp();int k = i;//保存最大性价比的物品下标for (int j = i; j < n; j++){if (max < g[j].getp()){max = g[j].getp();k = j;}}swap(g[i], g[k]);}double sum = 0;//背包总价值for (int i = 0; i < n; i++){if (bagW > g[i].getw())//背包容量大于物品重量{g[i].setc(1);//物品全部装入背包sum += g[i].getv();//背包价值增加bagW = bagW - g[i].getw();//剩余背包容量}else//背包容量大于物品重量{double x = double(bagW) / double(g[i].getw());g[i].setc(x) ;//装入物品的比例sum += g[i].getc() * g[i].getv();break;}}cout << "物品的最大价值为：" << sum << endl;for (int i = 0; i < n; i++){if (g[i].getc() != 0){if (g[i].getc() == 1)cout << "物品" << g[i].getn() << setw(20) << "价值为：" << g[i].getv() << endl;elsecout << "物品" << g[i].getn() << "装入了" << g[i].getc() <<setw(8)<< "   价值为：" << g[i].getv() << endl;}}return 0;
}//测试数据
//30 10
//4 3
//2 8
//9 18
//5 6
//5 8
//8 20
//5 5
//4 6
//5 7
//5 15//结果
//物品的最大价值为：70.5
//物品1            价值为：8
//物品9            价值为：15
//物品5            价值为：20
//物品2            价值为：18
//物品4            价值为：8
//物品7装入了0.25   价值为：6

查看全文

http://www.dinnco.com/news/52083.html